引力辅助是一种利用天体引力改变航天器速度的变轨方式,由于变轨过程无需消耗能量因而受到轨道设计者的广泛欢迎,目前已被应用于多项实际探测任务[1],如旅行者号、伽利略号、卡西尼号和尤利西斯号等。
然而,仅仅利用引力辅助,变轨效果有限,于是常常选择与其他变轨手段联合使用来增强变轨效果,形成了小推力引力辅助[2-3]、气动引力辅助[4-5]和带脉冲的引力辅助等变轨技术。
带脉冲的引力辅助变轨,即在引力辅助过程中施加脉冲,通过脉冲与天体引力的共同作用来达到变轨目的。对于不带脉冲的引力辅助,航天器相对于借力天体的轨道为双曲线[6]。文献[7-9]研究了二维引力辅助,文献[10-12]研究了三维引力辅助。若在引力辅助过程中施加脉冲,则航天器轨道在施加脉冲前后为两段不同的双曲线。
早在20世纪60年代,Gobetz[13]就研究了在双曲线轨道中施加单次或4次脉冲的最优转移问题,指出绕飞天体的半径是优化中必须考虑的约束条件,重点研究了约束条件下的最优转移。Walton等[14]肯定了文献[13]中约束条件的提法,研究了2个给定的双曲线超越速度向量之间的轨道转移。
1996年,Prado[15]首次对带脉冲的引力辅助变轨给出了简洁、清晰的描述。文献[15]用5个参数对变轨进行描述,推导了航天器速度、能量、角动量变化量与参数之间的关系式;给出了特定参数下施加脉冲的最优方向;比较了施加脉冲的2种方式,结果表明大多数情况下在近拱点施加脉冲比在引力辅助结束后施加脉冲更加高效。
此后,绝大部分轨道设计文献都将施加脉冲的位置选择在近拱点。文献[16]研究了在近拱点施加脉冲的平面引力辅助的优化问题。文献[17]研究了在近拱点施加脉冲的三维引力辅助,但只适用于小脉冲,当脉冲大于航天器速度1%时不成立。文献[18]研究了利用多次引力辅助的土星探测轨道的优化问题,若在引力辅助过程中需要施加脉冲,则在近拱点施加。文献[19]研究了飞越月球的引力辅助轨道,施加脉冲的位置在近拱点。也有一些文献施加脉冲的位置不在近拱点,如文献[20]选择在引力辅助结束后施加,但根据文献[15]的结论,这种方式往往并不高效。
综上所述,关于施加脉冲的位置,文献[15]仅仅比较了2个特殊位置,表明近拱点多数情况下优于引力辅助的结束点,但尚没有研究表明近拱点优于引力辅助过程中的其他位置。因此,虽然在目前的轨道设计中一般选择在近拱点施加脉冲,但其实是缺乏理论根据的。
为了研究引力辅助过程中施加脉冲的最优位置,本文引入一个参数表征施加脉冲的位置,推导航天器速度、能量与参数的函数关系,以能量增加最大为目标进行参数优化,可以求得施加脉冲的最优位置。结果表明,最优位置一般并不在近拱点。
1 在任意位置施加脉冲的引力辅助
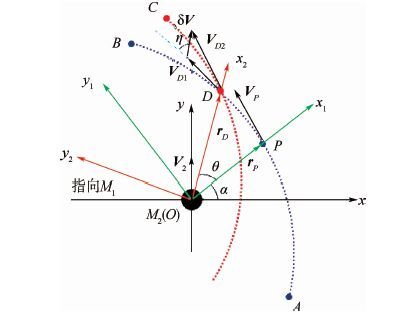
图 1所示为在任意位置施加脉冲的引力辅助变轨。天体M2绕天体M1运动。航天器从A点进入M2的影响球(如果不施加脉冲,航天器将沿双曲线轨道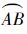
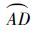
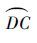
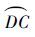
|
| 图 1 在任意位置施加脉冲的引力辅助变轨 Fig. 1 Swing-by maneuver applying an impulse at any arbitrary position |
在本文中,带脉冲的平面引力辅助可以通过6个独立参数来描述:①VP为第1段轨道
各角度均以逆时针方向为正。
为了推导上的方便,本文建立一组坐标系,如图 1所示。坐标系如下:
1)直角坐标系xOy 以M2质心为原点;x轴为M1和M2的连线;y轴为M2速度方向;V2为M2的速度。
2)直角坐标系x1Oy1 以M2质心为原点;x1轴、y1轴分别与rP、VP平行;VD1和VD2分别为施加脉冲前后航天器在D点的速度。
3)直角坐标系x2Oy2 以M2质心为原点;x2轴沿rD方向,y2轴与x2轴垂直。
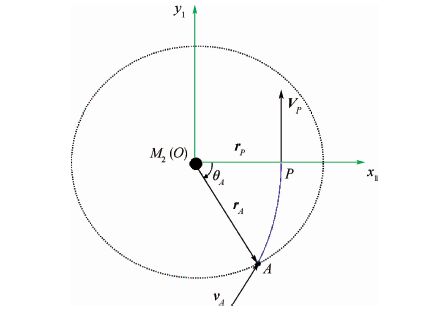
2 公式推导 2.1 计算航天器在A点的速度和矢径当航天器处于M2影响球内时,由轨道动力学可知,航天器相对于M2的轨迹为双曲线。如图 2所示。
|
| 图 2 第1段轨道 Fig. 2 The first section of orbit |
为了计算方便,首先在x1Oy1坐标系中研究。由近拱点P的数据可计算航天器在A点相对于M2的速度vA和矢径rA,rP和rA分别为rP和rA的大小(图 2为示意图,真实情况中rP与rA相比很小)。
Step 1 计算vA的大小
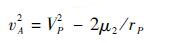
|
得到
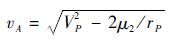
|
(1) |
式中:μ2为M2的引力参数;VP和rP分别为VP和rP的大小。
Step 2 计算vA与VP的夹角δ1
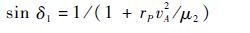
|
得到
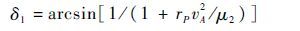
|
(2) |
Step 3 求vA
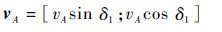
|
(3) |
Step 4 计算轨道的偏心率e1、单位相对角动量h1
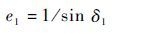
|
(4) |
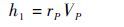
|
(5) |
Step 5 计算x1轴与rA的夹角θA
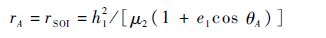
|
式中:rSOI为M2的影响球半径。
得到
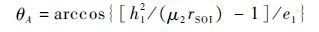
|
(6) |
Step 6 求rA
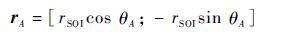
|
(7) |
Step 7 求vA、rA在坐标系xOy中的坐标表示转换矩阵为
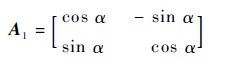
|
(8) |
得到
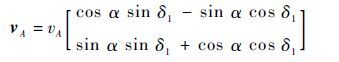
|
(9) |
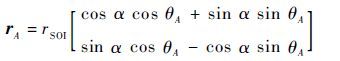
|
(10) |
Step 8 计算航天器在A点的绝对速度,记为Vin
航天器在A点的绝对速度为相对于M2的速度vA与M2的速度V2的矢量和。
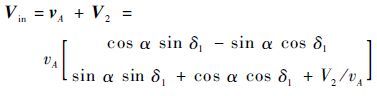
|
(11) |
在任意点D施加脉冲,D点的位置用θ表征。θ为rP与rD的夹角,逆时针为正,顺时针为负。
施加脉冲之前,航天器在D点的速度记为VD1,VD1在径向的投影为VrD1,在垂直于径向的投影为V⊥D1。施加脉冲δV的方向用η表征。施加脉冲之后,航天器的速度变为VD2,见图 3。
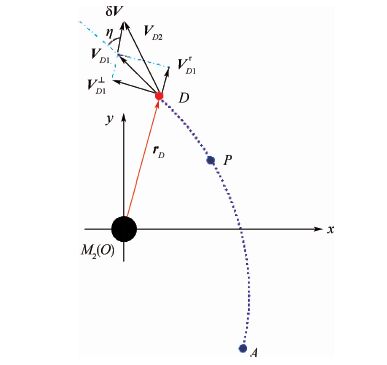
|
| 图 3 施加脉冲之后的航天器速度 Fig. 3 Velocity of spacecraft after impulse is applied |
Step 1 计算rD
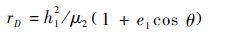
|
(12) |
Step 2 计算VrD1、V⊥D1、VD1的大小和VD1与V⊥D1的夹角ξ
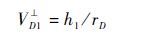
|
(13) |
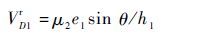
|
(14) |
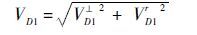
|
(15) |
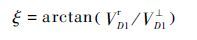
|
(16) |
Step 3 计算VD2
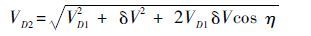
|
(17) |
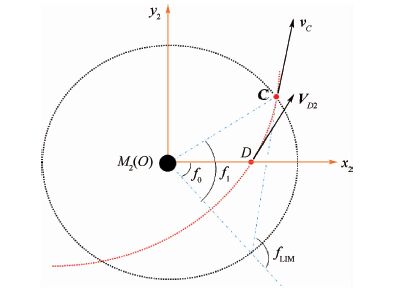
之后航天器沿轨道DC运动从C点离开M2的影响球,如图 4所示。首先在x2Oy2坐标系中研究。
|
| 图 4 第2段轨道 Fig. 4 The second section of orbit |
Step 1 计算vC的大小
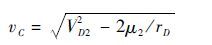
|
(18) |
Step 2 计算第2段双曲线轨道的半长轴a2
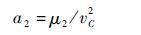
|
(19) |
Step 3 计算角动量h2、半正交弦p2、偏心率e2
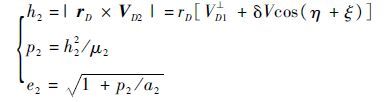
|
(20) |
Step 4 计算施加脉冲之后的双曲线轨道中航天器的真近点角f0
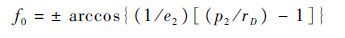
|
(21) |
f0的正负选取规则:VrD2=VrD1+δVsin(η+ξ),若VrD2>0,则航天器已经飞过近拱点,所以真近点角为正;若VrD2<0,航天器正飞向近拱点,所以真近点角为负。
Step 5 由e2计算fLIM(第2段双曲线轨道的渐近线和近拱点方向的夹角)
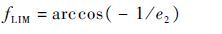
|
(22) |
Step 6 得到vC
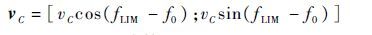
|
(23) |
Step 7 计算f1
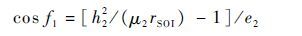
|
(24) |
Step 8 得到rC
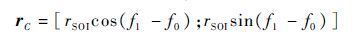
|
(25) |
记 δ2=fLIM-f0,θC=f1-f0,式(23)和式(25)可以表示为
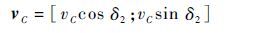
|
(26) |
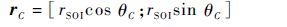
|
(27) |
Step 9 求vC、rC在坐标系xOy中的坐标表示转换矩阵为
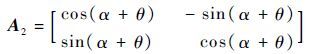
|
(28) |
得到
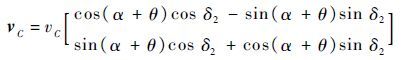
|
(29) |
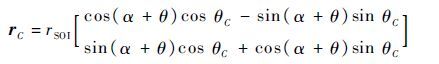
|
(30) |
Step 10 计算航天器在C点的绝对速度,记为Vout
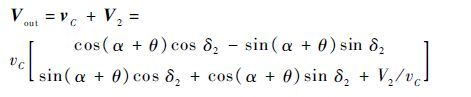
|
(31) |
航天器速度变化为
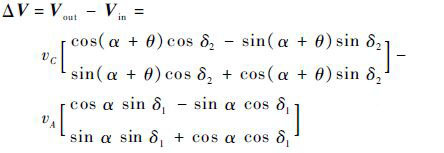
|
(32) |
航天器能量变化为
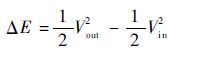
|
(33) |
航天器相对于借力天体的角动量改变为
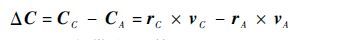
|
(34) |
指定借力天体之后,μ2、rSOI可通过查找天文数据得到。以上公式只是关于6个引力辅助参数的函数。特别地,当参数θ(表征施加脉冲的位置)变动时,ΔE会相应变动,可以用来研究施加脉冲的最优位置。
3 施加脉冲的最优位置以借助木星引力辅助为例。进行无量纲化处理,以木星平均轨道半径为单位长度。查找天文数据可得木星的μ2=9.5384×10-4,rSOI=6.1986×10-2。
设置参数:vP=6.0,rP=1.37595×10-4,α=90°;θ∈[-θA,θA],θA可由式(6)求得,本例中θ∈[-103.6°,103.6°];设置δV=1.0。η∈[-180°,180°]。
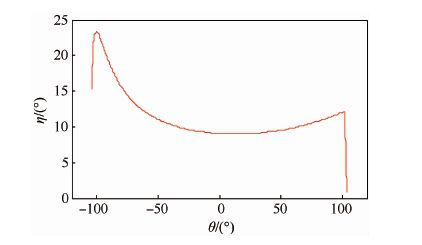
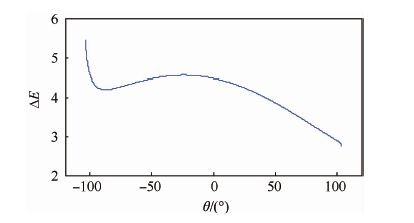
进一步,当θ取特定值时,ΔE只是关于η的函数,可以求得该位置处施加脉冲的最优方向。图 5所示为不同位置处施加脉冲的最优方向。由图 5可知,施加脉冲的最优方向与施加脉冲的位置有关,且与该位置处的速度方向并不一致。这样,可以求得在不同位置处分别施加各自最优方向的脉冲时所引起的能量改变,见图 6。图 6中,当施加脉冲的最优位置θoptimal=θA=-103.6°时,ΔE取得最大值,为5.422;近拱点(θ=0°)处ΔE=4.478。表明:施加脉冲的最优位置并不是近拱点,在最优位置施加脉冲比在近拱点施加脉冲高效21%。
|
| 图 5 不同位置处施加脉冲的最优方向 Fig. 5 Optimal directions to apply an impulse in different positions |
|
| 图 6 ΔE随θ的变化 Fig. 6 Variation of ΔE with θ |
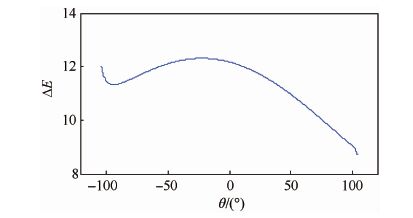
本例中施加脉冲的最优位置是引力辅助的开始位置,但开始位置并不总是最优位置,最优位置随参数的变化而变化。当vP、rP、α与图 6设置相同,δV的取值由1.0变为2.0时,结果如图 7所示。施加脉冲的最优位置变为θoptimal=-22.1°。
|
| 图 7 ΔE随θ的变化(δV=1.0~2.0) Fig. 7 Variation of ΔE with θ(δV=1.0-2.0) |
1) 本文通过引入一个参数表征施加脉冲的位置,将带脉冲的引力辅助变轨用6个参数来刻画,导出了变轨之后航天器的能量变化与参数的函数关系。
2) 以能量增加最大为优化目标,对施加脉冲的位置进行了优化。结果表明:施加脉冲的最优位置一般并不在近拱点,而且随其他参数的变化而变化。
3) 在最优位置施加脉冲与在近拱点施加相比,在某些情况下可高效20%以上。
在轨道设计中,可以首先利用本文公式确定施加脉冲的最优位置和最优方向,然后在最优位置按最优方向施加脉冲,可以提高脉冲的变轨效果。
| [1] | PRADO A F B A. A study of swing-by trajectories in the Galilean satellites of Jupiter[J]. Journal of Physics:Conference Series,2013, 465 : 012002 . |
| Click to display the text | |
| [2] | CAI X S, LI J F, GONG S P. Solar sailing trajectory optimization with planetary gravity assist[J]. Science China-Physics Mechanics & Astronomy,2015, 58 (1) : 1 –11. |
| Click to display the text | |
| [3] | CARNELLI I, DACHWALD B, VASILE M. Evolutionary neurocontrol: A novel method for low-thrust gravity-assist trajectory optimization[J]. Journal of Guidance,Control and Dynamics,2009, 32 (2) : 615 –624. |
| Click to display the text | |
| [4] | ARMELLIN R, LAVAGNA M, ERCOLI-FINZI A. Aero-gravity assist maneuvers: Controlled dynamics modeling and optimization[J]. Celestial Mechanics and Dynamical Astronomy,2006, 95 (1) : 391 –405. |
| Click to display the text | |
| [5] | MAZZARACCHIO A. Flight-path angle guidance for aerogravity-assist maneuvers on hyperbolic trajectories[J]. Journal of Guidance,Control and Dynamics,2015, 38 (2) : 238 –248. |
| Click to display the text | |
| [6] | BROUCKE R A.The celestial mechanics of the gravity assist[C]//AIAA/AAS Astrodynamics Conference.Reston:AIAA,1988:69-78. |
| Click to display the text | |
| [7] | PRADO A F B A. Close-approach trajectories in the elliptic restricted problem[J]. Journal of Guidance,Control and Dynamics,1997, 20 (4) : 797 –802. |
| Click to display the text | |
| [8] | 乔栋, 崔平远, 崔祜涛. 基于圆型限制性三体模型的借力飞行机理研究[J]. 宇航学报,2009, 30 (1) : 82 –87. QIAO D, CUI P Y, CUI H T. Research on gravity-assist mechanism in circular restricted three-body model[J]. Journal of Astronautics,2009, 30 (1) : 82 –87. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 乔栋, 崔平远, 尚海滨. 基于椭圆型限制性三体模型的借力飞行机理研究[J]. 宇航学报,2010, 31 (1) : 36 –43. QIAO D, CUI P Y, SHANG H B. Research on gravity-assist mechanism based on three-dimension elliptic restricted three-body model[J]. Journal of Astronautics,2010, 31 (1) : 36 –43. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | FELIPE G, PRADO A F B A. Classification of out-of-plane swing-by trajectories[J]. Journal of Guidance,Control and Dynamics,1999, 22 (5) : 643 –649. |
| Click to display the text | |
| [11] | 贾建华, 王琪. 三维引力辅助机理分析[J]. 北京航空航天大学学报,2012, 38 (7) : 981 –986. JIA J H, WANG Q. Research on gravity-assist mechanism based on three-dimension elliptic restricted three-body model[J]. Journal of Beijing University of Aeronautics and Astronautics,2012, 38 (7) : 981 –986. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | 贾建华, 王琪. 三维引力辅助解析分析方法研究[J]. 力学学报,2013, 45 (3) : 412 –420. JIA J H, WANG Q. An analytical study of gravity assist in three dimensions[J]. Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (3) : 412 –420. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | GOBETZ F W. Optimal transfers between hyperbolic asymptotes[J]. AIAA Journal,1963, 1 (9) : 2034 –2041. |
| Click to display the text | |
| [14] | WALTON J M, MARCHAL C, GULP R D. Synthesis of the types of optimal transfers between hyperbolic asymptotes[J]. AIAA Journal,1975, 13 (8) : 980 –988. |
| Click to display the text | |
| [15] | PRADO A F B A. Powered swing by[J]. Journal of Guidance,Control and Dynamic,1996, 19 (5) : 1142 –1147. |
| Click to display the text | |
| [16] | CASALINO L, COLASURDO G, PASTRONE D. Simple strategy for powered swing by[J]. Journal of Guidance,Control and Dynamic,1999, 22 (1) : 156 –159. |
| Click to display the text | |
| [17] | PRADO A F B A, FELIPE G. An analytical study of the powered swing-by to perform orbital maneuvers[J]. Advances in Space Research,2007, 40 (1) : 102 –112. |
| Click to display the text | |
| [18] | ZHU K J, LI J F, BAOYI H X. Multi-swing by optimization of mission to Saturn using global optimization algorithms[J]. Acta Mechanica Sinica,2009, 25 (6) : 839 –845. |
| Click to display the text | |
| [19] | FERREIRA A F D S, PRADO A F B A, WINTER O C. A numerical study of powered swing-bys around the moon[J]. Advances in Space Research,2015, 56 (2) : 252 –272. |
| Click to display the text | |
| [20] | 侯艳伟, 岳晓奎, 张莹. 基于脉冲机动的引力辅助深空探测轨道设计[J]. 西北工业大学学报,2012, 30 (4) : 491 –496. HOU Y W, YUE X K, ZHANG Y. Design of gravity-assist trajectory based impulsive maneuver[J]. Journal of Northwestern Polytechnical University,2012, 30 (4) : 491 –496. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |



