时滞微分系统的稳定性研究在理论和应用上都有其重要的意义,特别地,从控制理论的角度看,生物系统全时滞稳定即表明该系统对于时滞具有很好的鲁棒性和可靠性.
长期以来,人们一直致力于寻找时滞微分系统全时滞稳定的代数判据,已取得了不少进展.秦元勋在文献[1]中第1次将单滞后多维系统的全时滞稳定判据由超越形式的检验转化为代数形式的检验,并对n=1,2(n为非线性时滞微分系统的维数)的情形具体给出了判定法则,虽然此方法对高维情形处理起来并不容易.在文献[2]中,秦元勋和俞元洪根据Newton递推公式,对单时滞n=2的情况进行了深入的研究.文献[3]讨论了一类线性定常时滞系统全时滞渐进稳定的充分代数判据.文献[4, 5]研究了单时滞线性系统渐进稳定的代数判据;在文献[5]的基础上,文献[6]讨论了多时滞线性系统渐进稳定性的代数判据.文献[1, 2, 3, 4, 5, 6]中的方法均针对线性系统,并均使用传统的数学推导方法.模拟生物问题的动力系统通常是非线性的,较为复杂,利用传统的数学方法很难分析其稳定性,需要借助更先进的计算方法和工具.随着计算机科学与技术的发展,以精确计算为特点的符号计算逐渐成熟和完善,效率也逐步提高,成为数值计算的一种强有力的替代.
针对含参数的非线性生物系统,本文给出时滞微分系统全时滞稳定性的代数判据,研究如何利用符号计算方法分析多维生物系统正平衡点的渐进稳定性.文献[7, 8]提出了利用代数方法分析生物系统稳定性和分岔等问题的算法化方法,并且给出了软件实现及实验结果.不同于传统的数学推导,符号计算使得求解生物系统的稳定性和分岔更加程序化和自动化.本文在作者工作的基础上,进一步研究如何利用符号计算方法,如文献[9]中的三角分解、文献[10, 11]中的Grbner基和文献[12]中的实解分类等方法,程序化地分析生物系统全时滞稳定性.
1 时滞微分系统正平衡点的稳定性考虑如下n维非线性多时滞微分系统:
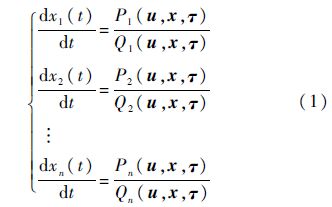
为了计算式(1)的正平衡点,令τ=0,可得
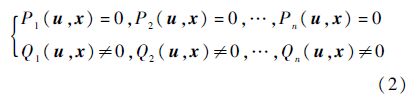
令y=x-x*,代入式(1)中,x*是系统的正平衡点,满足式(2),可得线性化之后的系统:

式(3)的特征方程为

时滞微分式(3)系统的全时滞稳定性,即多项式Δ(λ,τ)对∀τ∈R+均Hurwitz稳定.据文献[14],有
引理1 式(3)系统全时滞稳定的充分必要条件为
1) det[λI-A-$\sum\limits_{k=1}^{n}{{{A}_{k}}}$]=0的根具有负实部.
2) 对∀τ>0及任意实数y,都有

对于条件1): 令多项式M为
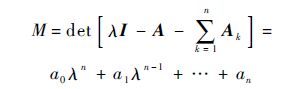

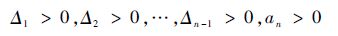
对于条件2):对∀τ>0及任意y,有

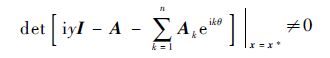
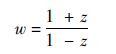
条件2)等价于: 对∀z∈R及任意实数y∈R-{0},都有

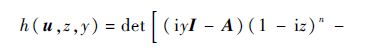
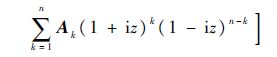
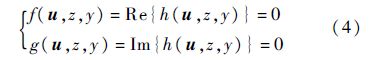
引理2 式(1)系统正平衡点全时滞稳定的充分必要条件是式(5)系统有正实根且式(6)系统无实根:
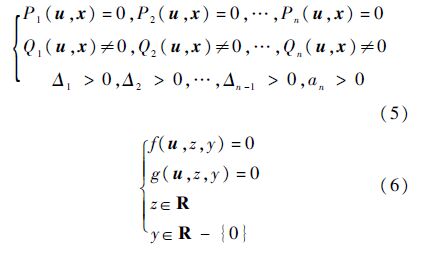
第2节描述了如何将时滞系统的全时滞稳定性问题化为代数问题,这里将研究如何将代数方法应用到求解这些代数问题上.
步骤1 构造半代数系统.
假设实际问题由式(1)系统来模拟,通过计算可得到含多项式方程及不等式的式(5)系统和式(6)系统.变元x及参数u可能需满足一些实际问题中的附加约束:

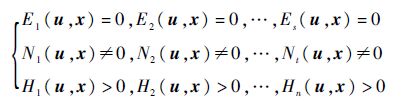
步骤2 计算三角列.
通过三角列或Grbner基方法,可以把多项式集E={E1,E2,…,Es}三角化,得到三角列Tk.若参数u出现,转至步骤4.
步骤3 参数不出现.
如果参数u不出现,可以用长度可无限小的有理区间来隔离每个Tk的实零点.令F={N1,N2,…,Nt,H1,H2,…,Hn}为不等式多项式集.然后F中的多项式在每个实零点上的符号可以通过计算它们在有理区间的端点的值来确定.由此得到用有理区间隔离的半代数系统Ψ的实解.
步骤4 实解分类.
假设参数u出现,令F对于每个三角列Tk,可利用F来计算一个关于u的代数簇V,使得其将实参数空间Rm分为有限多个胞腔,满足在每个胞腔上,Tk的实零点个数以及F在这些零点处的符号不变.从每个胞腔中取一个有理样本点,代入Tk消去参数,由步骤3可计算Tk的实零点以及F在该样本点的符号.
步骤5 参数条件最后,根据多项式在Ψ具有指定个数的实解的胞腔中样本点处的符号,建立参数u所需要满足的条件.
在文献[16]实解分类软件DISCOVERER的基础上,算法步骤(见图 1)已在MAPLE中实现.

|
| 图 1 代数方法分析算法步骤 Fig. 1 Algorithmic steps using algebraic approaches |
文献[13]中介绍了一种重要的生物模型:Lotka-Volterra捕食-食饵系统.为了验证本文中代数方法的可行性,使用这个简单的捕食-食饵系统演示利用符号计算方法分析全时滞稳定性的流程.在此,考虑以下单时滞的捕食-食饵系统:
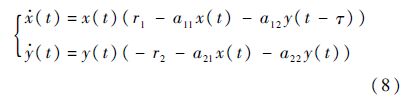
第1步 分析正平衡点及线性化.
令τ=0,那么平衡点问题可化为

考虑2×2阶Jacobian矩阵
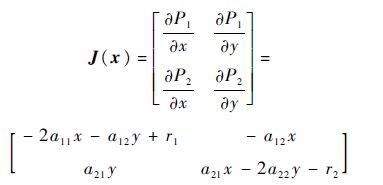
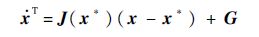
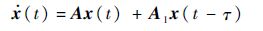
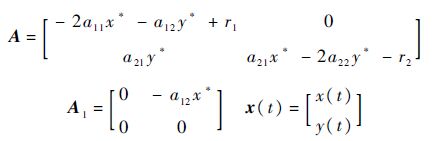
第2步 分析条件1).
第2节引理1中的条件1)是det[λI-A-A1]=0均具有负实根,在此,

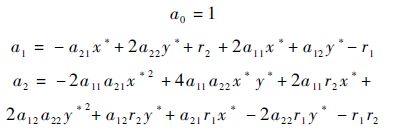
由多项式系数a0、a1、a2组成的Hurwitz判据
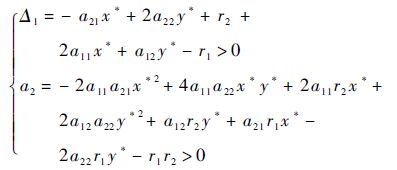
故而,可得半代数系统
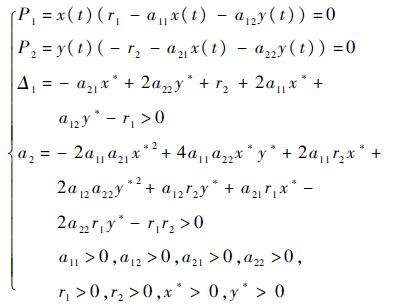
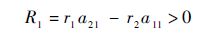
第3步 分析条件2). det[iyI-A-A1e-iyτ]x=x*≠0成立.
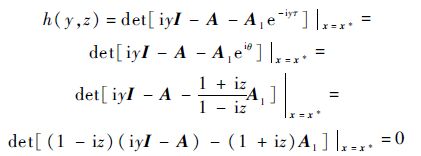
分离h(y,z)的实部和虚部可得半代数系统

求解该半代数系统可得
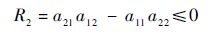
综上可得,当参数满足
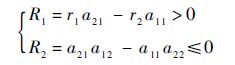
文献[17]中的无选择收获的Lotka-Volterra捕食-食饵系统也是一种重要的数学生物模型.考虑以下二维系统:
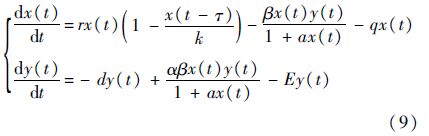
第1步 利用线性化方法和Hurwitz判据可得半代数系统,即条件1):

求解该半代数系统可得
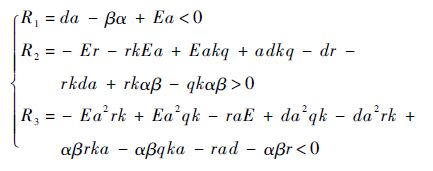
第2步 分析条件2).
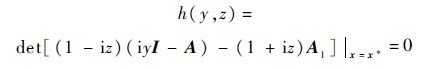
分离h(y,z)的实部和虚部可得半代数系统
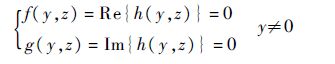
f(y,z)和g(y,z)都是含有参数和变量的多项式.表 1中是f(y,z)和g(y,z)的项数和最高次数,该问题使用传统的数学计算方法很难得出结果,而利用符号计算方法在几秒之内,可得
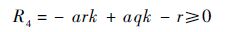
| 多项式 | 项数 | 最高次数 |
| f(y,z) | 62 | 9 |
| g(y,z) | 44 | 8 |
所以,当参数满足
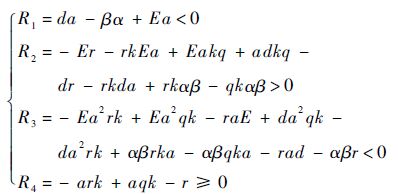
4.3 SIR传染病模型
SIR传染病模型是一个重要的生物模型,Cooke在文献[18]中提出了时滞SIR传染病模型,并指出t时刻的传染能力为βS(t)I(t-τ′),其中,β>0为每天每个感染者接触的人数,τ′≥0为病毒在被感染者体内的作用时间.文献[19]中时滞SIR传染病系统为
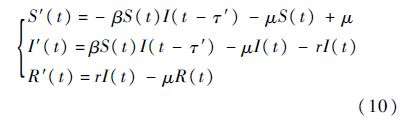
第1步 构造及分析条件1).
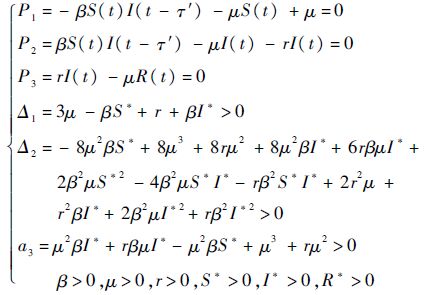
计算可得
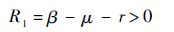
第2步 分析条件2).
分离h(y,z)的实部和虚部可得半代数系统<
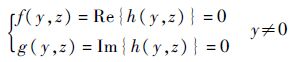
因此,当参数满足R1=β-μ-r>0 时,式(10)系统在平衡点处全时滞稳定.
5 结 论本文在Gröbner基、三角化分解和实解分类等符号计算原理基础上提出了一种新的验证生物系统全时滞稳定性的算法.
1) 经实验验证表明该算法可实现较为优异的计算性能,例如计算含有62项的多项式所用时间仅仅为几秒,这是传统的数学计算所达不到的.
2) 此外,仍在进行任意多时滞微分系统的全时滞稳定性分析的算法研究及实验.
| [1] | 秦元勋.有时滞的系统的无条件稳定性[J].数学学报,1960,10(1):125-142. Chin Y S.Unconditional stability of systems with time lags[J].Acta Mathematica Sinica,1960,10(1):125-142(in Chinese). |
| Cited By in Cnki (10) | Click to display the text | |
| [2] | 秦元勋,俞元洪.一类时滞微分系统无条件稳定的条件[J].控制理论与应用,1984,1(1):23-35. Chin Y S,Yu Y H.Unconditional stability conditions for a class of differential systems with time delay[J].Journal of Control Theory and Applications,1984,1(1):23-35(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [3] | 周超顺,邓聚龙.线性定常时滞系统全时滞渐近稳定的充分代数判据[J].自动化学报,1990,16(1):62-65. Zhou C S,Deng J L.A sufficient algebra criteria for stability of linear constant time-delay system[J].Acta Automatica Sinica,1990,16(1):62-65(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [4] | Cao D Q,He P,Ge Y M.Simple algebraic criteria for stability of neutral delay-differential systems[J].Journal of the Franklin Institute,2005,342(3):311-320. |
| Click to display the text | |
| [5] | Hu G D,Hu G D,Cahlon B.Algebraic criteria for stability of linear neutral systems with a single delay[J].Journal of Computational and Applied Mathematics,2001,135(1):125-133. |
| Click to display the text | |
| [6] | He P,Cao D Q.Algebraic stability criteria of linear neutral systems with multiple time delays[J].Applied Mathematics and Computation,2004,155(3):643-653. |
| Click to display the text | |
| [7] | Niu W,Wang D.Algebraic analysis of bifurcation and limit cycles for biological systems[M].Berlin,Heidelberg:Springer,2008:156-171. |
| Click to display the text | |
| [8] | Niu W,Wang D.Algebraic approaches to stability analysis of biological systems[J].Mathematics in Computer Science,2008,1(3):507-539. |
| Click to display the text | |
| [9] | Wang D.Elimination methods[M].Berlin,Heidelberg:Springer,2001:193-224. |
| >Click to display the text | |
| [10] | Buchberger B.Gröbner bases:An algorithmic method in polynomial ideal theory[J].Multidimensional Systems Theory,1985:184-232. |
| Click to display the text | |
| [11] | Faugère J C.A new efficient algorithm for computing Gröbner bases (F4)[J].Journal of Pure and Applied Algebra,1999,139(1):61-88. |
| Click to display the text | |
| [12] | Yang L,Xia B.Real solution classification for parametric semi-algebraic systems[C]//Algorithmic Algebra and Logic[S.l.:s.n.],2005:281-289. |
| Click to display the text | |
| [13] | 宋永利,韩茂安,魏俊杰.多时滞捕食-食饵系统正平衡点的稳定性及全局Hopf分支[J].数学年刊:A辑,2005,25(6):783-790. Song Y L,Han M A,Wei J J.Stability and global Hopf bifurcation for a predator-prey model with two delays[J].Chinese Annals of Mathematics:Series A,2005,25(6):783-790(in Chinese). |
| Click to display the text | |
| [14] | Bhattacharyya S P,Chapellat H,Keel L H.Robust control-the parametric approach[M].New York:Prentice Hall PTR,1995:446-472. |
| Click to display the text | |
| [15] | Lancaster P,Tismenetsky M.The theory of matrices:With applications[M].Pittsburgh:Academic Press,1985:89-103. |
| Click to display the text | |
| [16] | Xia B.DISCOVERER:A tool for solving semi-algebraic systems[J].ACM Communications in Computer Algebra,2007,41(3):102-103. |
| Click to display the text | |
| [17] | Kar T K,Pahari U K.Non-selective harvesting in prey-predator models with delay[J].Communications in Nonlinear Science and Numerical Simulation,2006,11(4):499-509. |
| Click to display the text | |
| [18] | Cooke K L.Stability analysis for a vector disease model[J].Journal of Mathmatics,1979,9(1):31-42. |
| Click to display the text | |
| [19] | Meng X,Chen L,Wu B.A delay SIR epidemic model with pulse vaccination and incubation times[J].Nonlinear Analysis:Real World Applications,2010,11(1):88-98. |
| Click to display the text |



