2. 中国人民解放军91880部队, 青岛 266300
2. People's Liberation Army 91880 Unit, Qingdao 266300, China
加速试验作为快速评估产品寿命的一种有效手段已经被广泛应用.有效的加速试验应保证产品在所有加速应力下的失效机理具有一致性,否则无法正确外推出产品在正常应力下的寿命信息.因此,在利用加速数据进行寿命预测时,必须要判别产品在各加速应力下的失效机理是否具有一致性.
目前,失效机理一致性判别方法可分为两大类.第1类不需要建立产品的可靠性模型,而是根据产品在各应力下的退化路径的形状是否一致进行失效机理一致性判别.其中,文献[1]基于秩相关系数对产品退化轨迹的一致性进行判别;文献[2, 3, 4]分别利用灰色理论对退化轨迹一致性进行判别.第2类需要结合产品的可靠性模型进行失效机理一致性判别.其中,文献[5, 6, 7]分别使用了F统计量、Bartlett统计量结合对数正态分布、Gamma分布及威布尔分布研究了失效机理一致性判别方法;文献[8]提出了基于退化模型的失效机理一致性判别方法.
第1类判别方法主要应用在加速试验前,可利用摸底试验数据大体确定产品失效机理保持一致性的加速应力值范围.第2类判别方法主要应用在加速试验后,可通过大量加速试验数据建立准确的可靠性模型,进而判别产品在加速试验中的失效机理是否一致.然而,现有的第2类方法主要针对加速寿命试验,针对加速退化试验的研究较少.
为了解决加速退化试验中产品失效机理一致性判别难题,本文以性能退化服从Gamma过程的产品为例,提出了基于加速系数不变原则的失效机理一致性判别方法.首先分析了失效机理一致性判别的理论依据,其次引入加速系数不变原则推导出Gamma过程的参数在不同应力下应满足的变化规律,然后给出了利用t统计量进行参数一致性检验的方法,接下来通过仿真试验分别对加速系数不变原则的推导结论和基于t统计量的参数一致性检验方法进行了验证,最后将本文所提方法在步进应力加速退化试验中进行了实例应用.
1 失效机理一致性判别的理论依据周源泉等[9]研究了加速寿命试验中产品失效机理一致性的判别方法,他指出加速系数不变的充要条件是寿命分布模型的各参数在不同应力下满足特定的变化规律,文献[10]进一步指出失效机理不变是加速系数不变的充要条件.文献[5, 6, 7]以此为理论依据,结合不同的寿命分布模型研究了失效机理一致性判别方法.
利用加速系数不变原则同样可以推导出性能退化模型参数在不同应力下满足变化规律,由此可建立失效机理不变与性能退化模型参数之间的联系,如图 1所示.根据图 1中的等效关系可将失效机理一致性判别问题转换为性能退化模型参数检验问题.对于绝大多数性能退化模型来说,模型参数不止一个并且有的参数随着应力变化有的参数保持不变,构建的被检参数关系式应该与应力无关.

|
| 图 1 失效机理不变与性能退化模型参数之间的联系 Fig. 1 Relationships between failure mechanism consistency and model parameters |
由于产品的性能退化过程具有不确定性,随机过程适用于退化建模,其中Gamma过程被广泛用于对严格单调退化过程建模.如果随机过程{Y(t),t≥0}为Gamma过程,则{Y(t),t≥0}满足以下性质.
1) Y(t)在任两个不相交的时间区间内具有平稳独立增量ΔY(t)=Y(t+Δt)-Y(t).
2) ΔY(t)服从如下形式的Gamma分布:
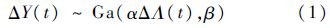
3) Y(t)在t=0处连续,且Y(0)=0.
使用Gamma过程{Y(t),t≥0}对产品退化过程建模,则Y(t)首次到达失效阈值D的时间为产品的寿命ξ=inf{tY(t)≥D}={tY(t)≥D}.根据Gamma分布的可加性,由式(1)可得Y(t)~Ga(αΛ(t),β),进而推导出产品的可靠度函数为


对于Gamma过程在加速退化试验中的应用,文献[11, 12]中假定α随着应力水平改变发生变化而β保持不变,但是文献[13, 14]中使用了完全相反的假定.以下利用加速系数不变原则推导Gamma过程参数的变化规律.
加速系数的一个定义为:设Fk(tk)和Fh(th)分别表示产品在任两个应力Sk和Sh下的累积失效概率(其中tk和th为其相应的试验时间),如有Fk(tk)=Fh(th),则可将应力Sk相当于应力Sh的加速系数Ak,h定义为

根据加速系数不变原则,加速系数Ak,h应为一个与可靠度无关的常数,即对任意tk下式(5)恒成立:
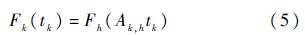
将式(3)代入式(5),并设时间函数为Λ(t)=t,得
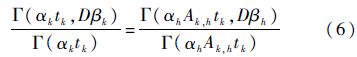
为了保证式(6)对任意tk恒成立,需要满足:

因此,以下关系可被推导出:

可知α应该随着应力的改变发生变化而β应该保持不变,此推导结论与文献[11, 12]中的假定相一致,也说明文献[13, 14]中的假定不合理.
当利用Gamma过程对非线性退化过程进行建模时,一般设时间函数Λ(t)=tr,其中r为时间参数.将Λ(t)=tr代入式(4)~式(8),可推导出以下关系式:
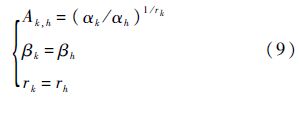
当利用Gamma过程对线性退化过程建模时,取Λ(t)=t,根据式(8)确定被检参数关系式为βk=βh;对非线性退化过程建模时,取Λ(t)=tr,根据式(9)确定被检参数关系式为βk=βh和rk=rh.下面针对非线性退化建模的情况研究参数一致性的假设检验方法.
设yijk(i=1,2,…,n;j=1,2,…,m;k=1,2,…,q)为应力Sk下第j个产品第i次测量得到的退化数据,tijk为对应的测量时刻,任一产品的参数估计值(αjk,βjk,rjk)可通过如下似然函数求解出:

考虑构建t统计量分别检验关系式βk=βh和rk=rh是否成立.当检验关系式βk=βh是否成立时,将β1,β2,…,βq作为检验样本,则任一应力Sk下的样本βk可看作出自同一总体,并且不同总体之间相互独立.由于产品间不可避免存在个体差异,每个产品的退化轨迹不尽相同,故性能退化模型的参数估计值也并不一致,呈现出在较小范围内围绕某一均值上下波动的特点.因此检验样本也具有类似的Normal分布特征,假设每个应力下的样本分别出自Normal分布总体,对两个Normal分布总体的样本是否具有相同的均值进行t统计量检验,进而判断出这两个总体的样本是否有显著差异.需要注意的是,使用t统计量应要求各应力下的样本量不小于10.基于t统计量的检验方法描述如下:
设X1,X2,…,Xn是来自N(μ1,σ2)的样本,Y1,Y2,…,Ym是来自N(μ2,σ2)的样本,原假设H0∶μ1=μ2,备选假设H1∶μ1≠μ2,建立如下t统计量

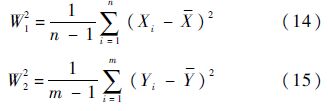
由于

当显著性水平为ρ时,原假设的拒绝域为

如果不同总体的样本之间没有显著差异,则可认为被检参数关系式成立,反之认为被检参数关系式不成立.只有当两个被检参数关系式βk=βh和rk=rh都成立时,方能说明产品在应力Sk和Sh下的失效机理具有一致性.
4 仿真验证 4.1 加速系数不变原则推导结果的验证第2节通过加速系数不变原则推导出了Gamma过程各参数的变化规律,本节通过仿真试验对推导结论式(9)进行验证[15],仿真模型为

仿真模型的参数值设置为:(a,b)=(2,1);β=1;i=1,2,…,10;j=1,2,…,20;tij=10,20,…,100;Λ(tij)=trij;r∈(0.5,1,2).验证步骤如下:
1) 利用仿真模型生成产品在应力Sk下的退化增量数据Δyijk,ΔΛ(tijk).
2) 利用式(10)解得Sk下的参数估计值αjk、βjk和rjk.
3) 设加速系数Ak,h∈(0.4,4),折算到Sh下的退化增量数据为Δyijh,ΔΛ(tijk·Ak,h).
4) 利用式(10)解得Sh下的参数估计值αjh、βjh和rjh.
5) 获得αjk/αjh、βjk/βjh和rjk/rjh的平均值,判断是否满足式(9)给出的关系式.
表 1显示βjk/βjh及rjk/rjh的均值几乎为1,并且(αjk/αjh)1/rjk的均值几乎等于Ak,h,考虑到数据处理过程中不可避免的数据舍入误差,这说明基于加速系数不变原则推导出的参数变化规律(式(9))是正确的.
| r | Ak,h=0.4 | Ak,h=4 | ||||

| ||||||
| 0.5 | 1.000 0 | 1.000 0 | 0.400 0 | 1.000 0 | 1.000 0 | 4.000 1 |
| 1 | 1.000 2 | 1.000 1 | 0.400 1 | 1.000 1 | 1.000 0 | 4.000 0 |
| 2 | 0.999 9 | 1.000 0 | 0.400 0 | 1.000 0 | 1.000 0 | 4.000 0 |
第3节提出了参数值一致性的假设检验方法,本节通过仿真试验对检验方法的有效性进行验证.根据文献[1],产品失效机理具有一致性时,其退化轨迹的形状也具有一致性.据此,首先通过时间函数Λ(t)=tr参数r的不同取值生成不同形状的退化数据,然后利用基于t统计量的检验方法进行参数一致性检验,以验证所提检验方法的有效性.仿真模型为

1) r取值为0.8并且设Ak,h=1,利用仿真模型生成Sk下的退化增量Δyijk,ΔΛ(tijk;r1),解出参数估计值βjk,rjk,得估计值向量βk,rk;
2) r分别取0.8,0.9,1,1.1,1.2,利用仿真模型生成随机应力Sh(h=1,2,3,4,5)下的退化增量Δyijk,ΔΛ(tij1;r1),Δyijk,ΔΛ(tij2;r2),…,Δyijk,ΔΛ(tij5;r5),分别解出参数估计值βj1,rj1,βj2,rj2,…,βj5,rj5,得估计值向量β1,r1,β2,r2,…,β5,r5;
3) 设显著性水平为0.05,将βk与βh进行一致性检验,rk与rh进行一致性检验,两次检验都通过方能证明产品在Sk与Sh下的失效机理具有一致性.
4) 将第1)步中的r依次取值为0.9,1,1.1,1.2,重复步骤1)~步骤3).
显著性水平为0.05时,t统计量拒绝域的下边界为t0.975(38)=2.024,检验结果如表 2所示.当步骤1)与步骤2)中的参数r取值相同时,所提检验方法准确检测出其参数估计值具有一致性;当两个步骤中的参数r分别取值为0.8,0.9,1时,所提检验方法能够准确检测出其参数估计值不具有一致性;当两个步骤中参数r的差值变为0.05时,例如取值为1,1.05,1.1时,所提检验方法依然能够准确检测出参数估计值不具有一致性.仿真试验结果说明本文所提的基于t统计量的参数一致性检验方法是有效的.
| r | 0.8 | 0.9 | 1 | 1.05 | 1.1 |
| 0.8 | 通过 | 未通过 | 未通过 | 未通过 | 未通过 |
| 0.9 | 未通过 | 通过 | 未通过 | 未通过 | 未通过 |
| 1 | 未通过 | 未通过 | 通过 | 未通过 | 未通过 |
| 1.05 | 未通过 | 未通过 | 未通过 | 通过 | 未通过 |
| 1.1 | 未通过 | 未通过 | 未通过 | 未通过 | 通过 |
某型军用电连接的接触件为表面镀金的铜合金基体,由于工作环境的原因,此型电连接器寿命受温度和湿度的影响较大,温度和湿度可促使接触件表面的氧化物加速生成,氧化物的堆积促使接触电阻不断增大最终导致产品失效[16].已知此型电连接器的机械寿命为插拔500次以上,通过步进应力加速退化试验对其电气寿命进行了研究,具体试验信息如下:
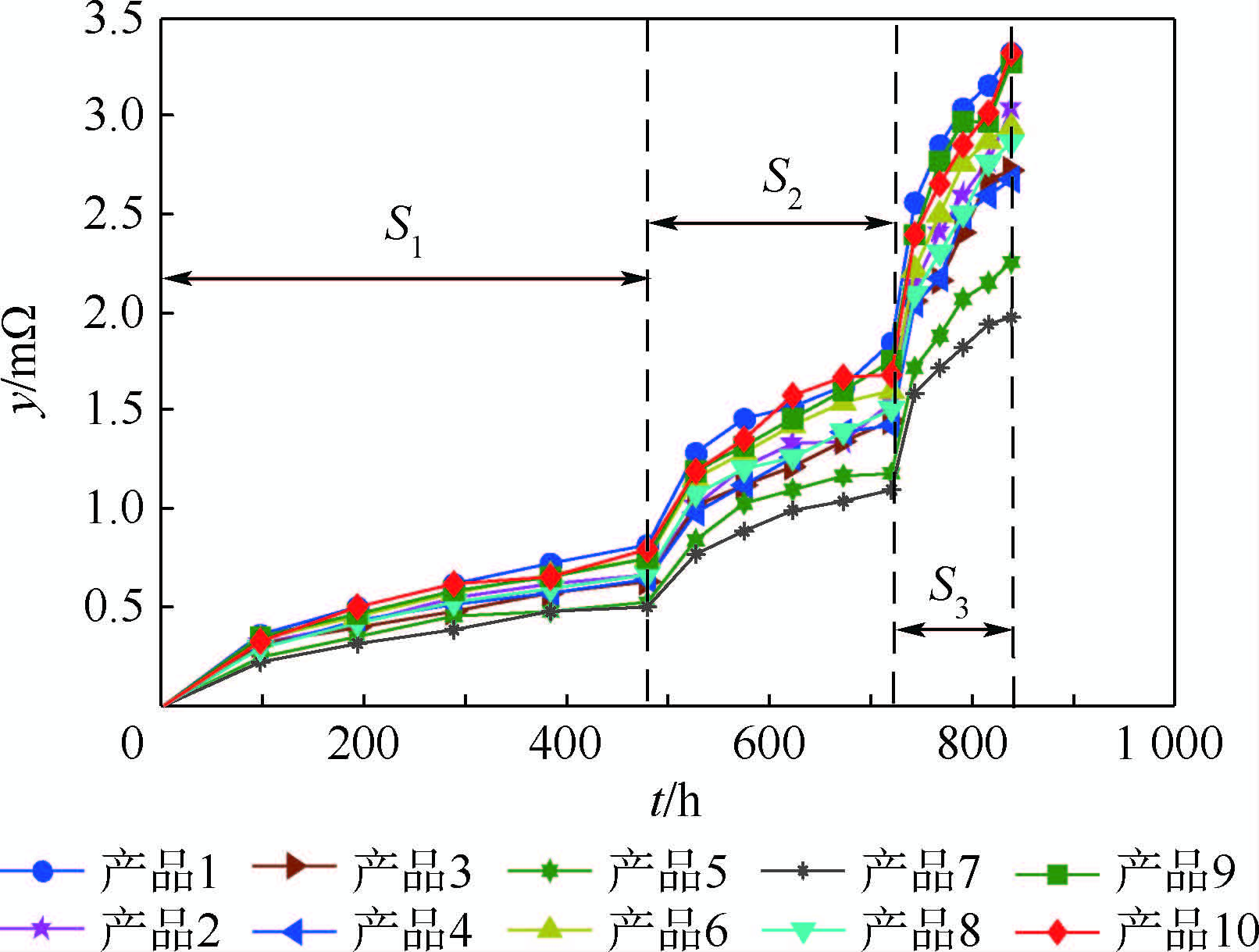
试验中设置温度、相对湿度3组综合加速应力S1(T1=75℃,RH1=70%),S2(T2=100℃,RH2=80%),S3(T3=125℃,RH3=90%).随机抽取10个产品,在每组加速应力下对10个产品进行等时间间隔测量,并且测量次数都为5次.S1下的测量间隔为96 h;S2下的测量间隔为48 h;在S3下的测量间隔为24 h.使用毫欧计对接触电阻进行测量,为了抵消每次测量不确定性的影响,将所有接触件的平均接触电阻作为退化量.测量数据如图 2所示.
|
| 图 2 步进应力加速退化数据 Fig. 2 Step stress accelerated degradation data |
设tijk为整个加速试验中对应的测量时刻,zijk为Sk下对应的测量时刻,Δyijk=yijk-y(i-1)jk为退化增量,其中i=1,2,…,5;j=1,2,…,10;k=1,2,3.由于在初始时刻产品并不存在膜层电阻,导致接触电阻测量值很小且极不稳定,此时的测量值小于测量设备引入的不确定度,故将初始测量值y0jk统一为0.对3组加速应力下的测量数据处理时,依据以下折算关系:

首先对产品退化过程是否符合Gamma过程进行检验.根据文献[17],如果产品退化为Gamma过程,则3Δyijkβjk/(αjkΔΛ(tijk))应该近似服从一个均值为1-1/(9αjkΔΛ(tijk))方差为1/(9αjkΔΛ(tijk))的正态分布.据此,在对以上正态分布标准化后,分别代入每个产品在3个应力下的退化数据进行标准正态分布的假设检验,在显著性为0.05时,每个产品在各应力下的退化过程都服从Gamma过程.然后通过式(10)求得每个产品在各加速应力下的参数估计值βjk,rjk,如表 3所示.
| 编号 | S1 | S2 | S3 | |||
| βj1 | rj1 | βj2 | rj2 | βj3 | rj3 | |
| 1 | 0.053 1 | 0.520 | 0.032 5 | 0.501 | 0.035 1 | 0.445 |
| 2 | 0.026 1 | 0.467 | 0.061 9 | 0.498 | 0.010 7 | 0.585 |
| 3 | 0.016 2 | 0.446 | 0.006 5 | 0.492 | 0.057 1 | 0.452 |
| 4 | 0.007 7 | 0.482 | 0.010 7 | 0.492 | 0.030 2 | 0.437 |
| 5 | 0.026 8 | 0.461 | 0.024 8 | 0.395 | 0.006 1 | 0.427 |
| 6 | 0.008 5 | 0.505 | 0.004 5 | 0.453 | 0.016 7 | 0.444 |
| 7 | 0.040 1 | 0.518 | 0.004 6 | 0.458 | 0.007 6 | 0.350 |
| 8 | 0.020 4 | 0.521 | 0.018 4 | 0.464 | 0.012 3 | 0.529 |
| 9 | 0.010 2 | 0.498 | 0.007 5 | 0.546 | 0.040 8 | 0.398 |
| 10 | 0.044 6 | 0.563 | 0.040 3 | 0.443 | 0.019 1 | 0.530 |
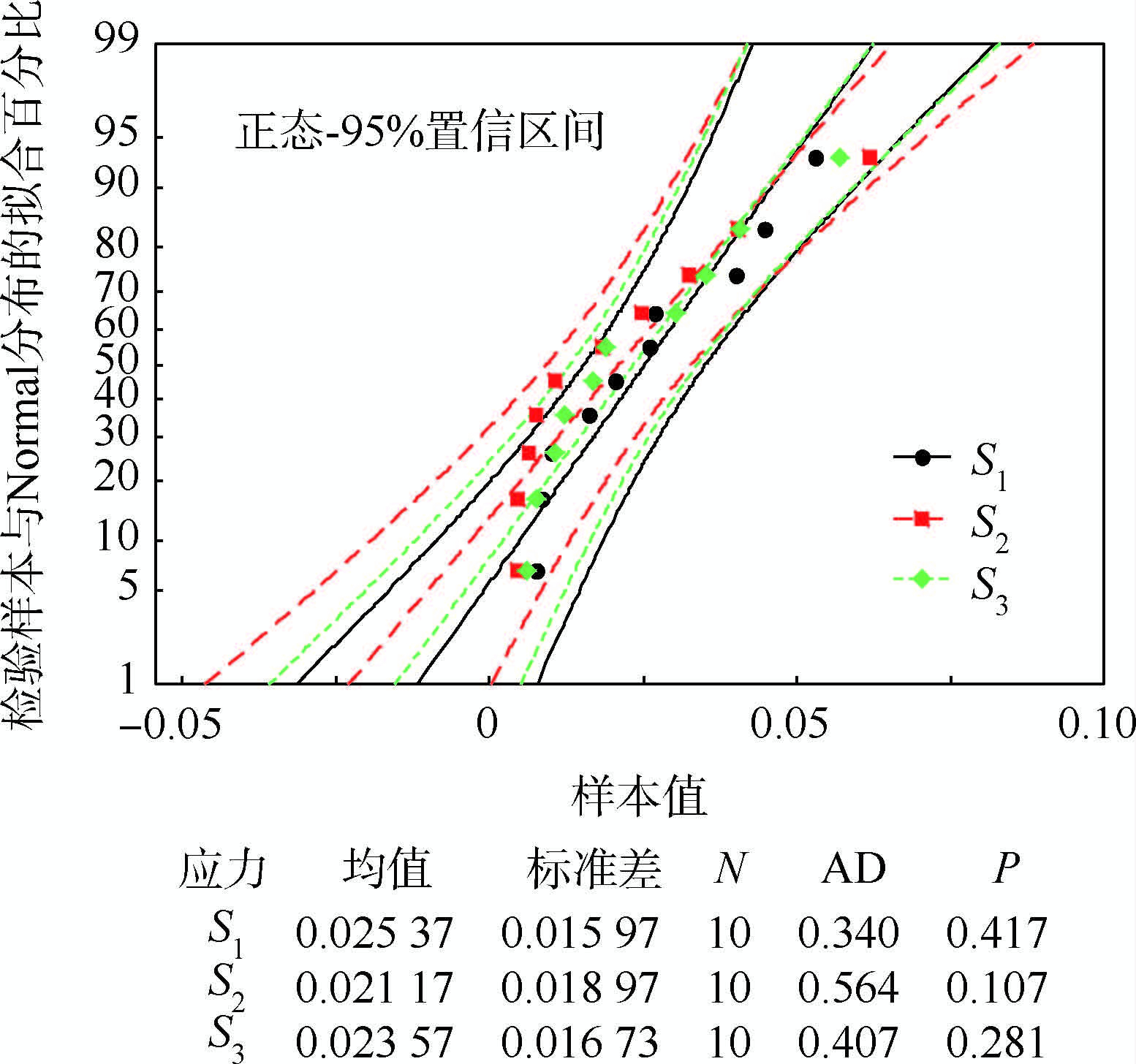
接下来利用Anderson-Darling统计量对样本βk和rk(k=1,2,3)分别进行Normal分布的假设检验,在显著性水平为0.05时接受βk、rk在各加速应力下服从Normal分布的原假设,图 3及图 4给出了检验样本与Normal分布的拟合情况.
|
| 图 3 βk在Normal分布下的拟合优度检验 Fig. 3 Goodness-of-fit test of βk under Normal distribution |

|
| 图 4 rk在Normal分布下的拟合优度检验 Fig. 4 Goodness-of-fit test of rk under Normal distribution |
最后利用基于t统计量的检验方法对各应力下样本的一致性进行假设检验.当显著性水平为0.05时,得拒绝域的下边界为t0.975(18)=2.101,逐一对任两个应力下的样本进行检验,结果如表 4所示.可知各加速应力下的检验样本没有显著差异,产品在S1、S2及S3下的失效机理具有一致性.
| 一致性检验 | 检验样本βk | 检验样本rk | ||||
| β1,β2 | β1,β3 | β2,β3 | r1,r2 | r1,r3 | r2,r3 | |
| t统计量 | 0.536 | 0.246 | 0.300 | 1.403 | 1.562 | 0.569 |
| 结论 | 通过 | 通过 | 通过 | 通过 | 通过 | 通过 |
为了解决加速退化试验中产品失效机理一致性判别难题,文本以Gamma退化模型为研究对象,提出了基于加速系数不变原则的失效机理一致性判别方法,主要研究结论如下:
1) 加速系数不变原则为确定性能退化模型的参数在不同加速应力下的变化规律提供了一种有效方法,不仅是失效机理一致性判别的基础而且可为正确进行加速退化建模提供指导.
2) 性能退化模型往往需要引入时间函数对非线性退化进行建模,此种情况下进行失效机理一致性判别还包括对时间参数的检验.本文提出了基于t统计量的方法对参数一致性进行假设检验,仿真试验表明此方法可有效判别出参数估计值是否具有一致性.
3) 本文提出的失效机理一致性判别方法可容易拓展到采用其他性能退化模型的情况,并且适用于各种加速试验方式,因此具有较广的适用范围和良好的工程应用性.
| [1] | 冯静.基于秩相关系数的加速贮存退化失效机理一致性检验[J].航空动力学报,2011,26(11):2439-2444. Feng J.Consistent test of accelerated storage degradation failure mechanism based on rank correlation coefficient[J].Journal of Aerospace Power,2011,26(11):2439-2444(in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [2] | 姚军,王欢,苏泉.基于灰色理论的失效机理一致性检验方法[J].北京航空航天大学学报,2013,39(6):734-738. Yao J,Wang H,Su Q.Consistency identification method of failure mechanism based on grey theory[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(6):734-738(in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [3] | 潘晓茜,康锐.基于灰色预测的加速试验机理一致性判别方法[J].北京航空航天大学学报,2013,39(6):787-791. Pan X Q,Kang R.Identification method of failure mechanism consistency for accelerated testing based on grey forecasting[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(6):787-791(in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [4] | 李晓刚,王亚辉.利用非等距灰色理论方法判定失效机理一致性[J].北京航空航天大学学报,2014,40(7):899-904. Li X G,Wang Y H.Identification method of failure mechanism consistency by non-equidistance grey theory model[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(7):899-904(in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [5] | 周源泉,翁朝曦.对数正态分布环境因子的统计推断[J].系统工程与电子技术,1996,18(10):73-81. Zhou Y Q,Weng C X.Statistical inferences of environmental factors for the lognormal distribution[J].System Engineering and Electronics,1996,18(10):73-81(in Chinese) |
| Cited By in Cnki (12) | Click to display the text | |
| [6] | 马小兵,王晋忠,赵宇.基于伪寿命分布的退化数据可靠性评估方法[J].系统工程与电子技术,2011,33(1):228-232. Ma X B,Wang J Z,Zhao Y.Reliability assessment using constant-stress accelerated degradation data based on pseudo life distribution[J].System Engineering and Electronics,2011,33(1):228-232(in Chinese) |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | 林逢春,王前程,陈云霞,等.基于伪寿命的加速退化机理一致性边界检验[J].北京航空航天大学学报,2012,38(2):233-238. Lin F C,Wang Q C,Chen Y X,et al.Pseudo-life-based test method of mechanism consistency boundary for accelerated degradation testing[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(2):233-238(in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [8] | 王浩伟,徐廷学,王伟亚.基于退化模型的失效机理一致性检验方法[J].航空学报,2015,36(3):889-897. Wang H W,Xu T X,Wang W Y.Test method of failure mechanism consistency based on degradation model[J].Acta Aeronautica et Astronautica Sinica,2015,36(3):889-897(in Chinese) |
| Cited By in Cnki | |
| [9] | 周源泉,翁朝曦,叶喜涛.论加速系数与失效机理不变的条件(Ⅰ):寿命型随机变量的情况[J].系统工程与电子技术,1996,18(1):55-67. Zhou Y Q,Weng C X,Ye X T.Study on accelerated factor and condition for constant failure mechanism(Ⅰ):The case for lifetime is a random variable[J].Systems Engineering and Electronics,1996,18(1):55-66(in Chinese) |
| Cited By in Cnki (47) | Click to display the text | |
| [10] | 杨宇航,周源泉.加速寿命试验的理论基础(Ⅰ)[J].推进技术,2001,22(4):276-278. Yang Y H,Zhou Y Q.Theoretical foundation of accelerated life(Ⅰ)[J].Journal of Propulsion Technology,2001,22(4):276-278(in Chinese) |
| Cited By in Cnki (35) | Click to display the text | |
| [11] | Park C,Padgett W J.Accelerated degradation models for failure based on Geometric Brownian motion and Gamma processes[J].Lifetime Data Analysis,2005,11(4):511-527 |
| Click to display the text | |
| [12] | Tseng S T,Balakrishnan N,Tsai C C.Optimal step-stress accelerated degradation test plan for Gamma degradation processes[J].IEEE Transactions on Reliability,2009,58(4):611-618 |
| Click to display the text | |
| [13] | Lawless J,Crowder M.Covariates and random effects in a Gamma process model with application to degradation and failure[J].Lifetime Data Analysis,2004,10(3):213-227 |
| Click to display the text | |
| [14] | Wang X.Nonparametric estimation of the shape function in a Gamma process for degradation data[J].The Canadian Journal of Statistics,2009,37(1):102-118 |
| Click to display the text | |
| [15] | Wang H W.Xu T X,Mi Q.Lifetime prediction based on Gamma processes from accelerated degradation data[J].Chinese Journal of Aeronautics,2015,28(1):172-179. |
| [16] | 王浩伟,徐廷学,赵建忠.融合加速退化和现场实测退化数据的个体寿命预测方法[J].航空学报,2014,35(12):3350-3357. Wang H W,Xu T X,Zhao J Z.Residual life prediction method fusing accelerated degradation data and field degradation data[J].Acta Aeronautica et Astronautica Sinica,2014,35(12):3350-3357(in Chinese) |
| Cited By in Cnki (5) | Click to display the text | |
| [17] | Wang X,Xu D.An inverse Gaussian process model for degradation data[J].Technometrics,2010,52(2):188-197 |
| Click to display the text |



