GO法(GO methodology)[1]是一种以成功为导向的系统概率分析技术,对于多状态、有时序的系统,尤其对有实际物流如气流、液流、电流等过程系统具有很强的可靠性、安全性建模描述能力.在工程系统中,组成部件和设备经常是可修复的,现有的可修算法[2]是以可修操作符的概率公式为基础,先求得可修系统的等效故障率和等效维修率,然后再考虑操作符之间的相关性参数,最终通过一系列转换求得等效操作符的可用度.在该方法中,如果输入信号存在共有信号则需先将共有信号分离出去[3],进行操作符逻辑计算后,再将共有信号合并,再考虑停工相关、维修相关等复杂参数.这些问题都影响了GO法在实际工程中的广泛应用.
动态贝叶斯网络(Dynamic Bayesian Networks,DBN)是建立在静态贝叶斯网络和Markov模型基础上的图形结构.因为其具有描述事件多态性和非确定性逻辑关系的能力且能够保证较高的精度,所以常用来分析有时序的动态复杂系统.自21世纪初,动态贝叶斯网络在可靠性领域中应用的愈加广泛.2003年,法国学者针对动态贝叶斯网络在复杂制造过程形式化建模的问题进行了研究[4];2005年,美国学者在对动态故障树的研究中加入了动态贝叶斯网络,使其能够更加完整地描述动态过程[5];2009年,文献[6]提出了基于动态贝叶斯网络节点的系统可靠性研究.
近年来,国内研究人员也对动态贝叶斯网络应用在可靠性中进行了深入的研究.2008年,文献[7]提出了基于动态贝叶斯网络的动态故障树分析方法,并给出了定量分析方法;2012年,动态贝叶斯网络被应用在配电系统的可靠性研究上,很好地描述了其保护装置的动态演变过程[8];经过进一步的研究发展,2014年,文献[9]基于T-S故障树和动态贝叶斯网络提出了模糊可靠性评估的新方法,解决了传统故障树无法描述节点间模糊性逻辑关系的缺点.目前,动态贝叶斯网络已在动态可靠性框图、Markov、故障树等可靠性模型中得以应用[10, 11, 12, 13, 14],但在可修GO法中并没有得到应用.
本文提出一种基于动态贝叶斯网络的方法,统一描述GO法模型中的静态和动态行为,简化GO法针对可修特性的算法过程.首先介绍了GO法可修理论和动态贝叶斯网络基本理论,给出操作符的动态贝叶斯网络映射规则,并针对操作符之间的相关性行为(停工相关、备份相关、维修相关)给出了定量计算公式.最后,结合案例说明算法的操作步骤,同时分析系统的可用度曲线及在给定时间点下的可靠性相关参数.
在本文提出的新算法中,无需考虑共有信号等问题,并且对于停工相关、维修相关、备件相关等可修动态特性也能进行统一的形式化描述,根据系统的基本结构情况,直接描述系统的静态和动态特性,并结合成熟算法,不仅可以得到每一时刻的可靠性参数,还可得到系统可用度的变化曲线,简化了GO法可修系统的计算过程,便于工程人员掌握和应用. 1 GO法与动态贝叶斯网络 1.1 GO法简介
系统中的元件、部件或子系统可以统称为单元,GO法中用操作符来代表单元,用信号流来表示功能单元输入S、输出信号R之间的逻辑关系.GO法模型中共有17类操作符[2],如图 1所示.根据操作符的作用和运算规则不同,将操作符分为两大类型:
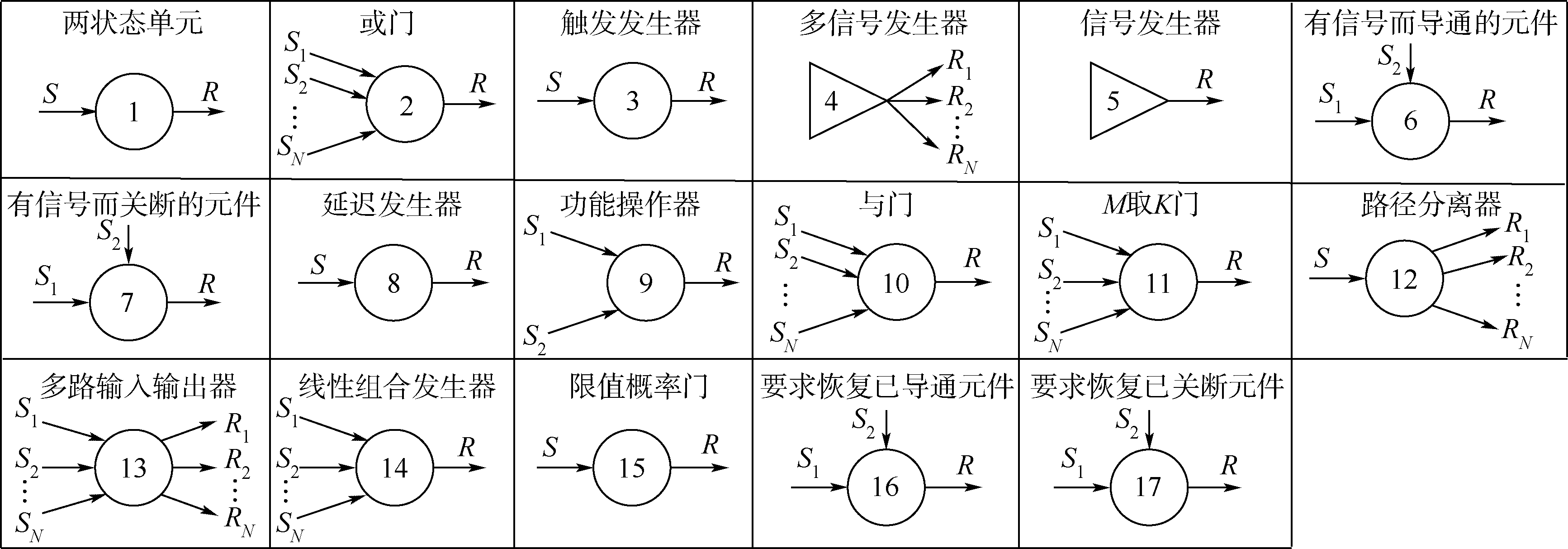 |
| 图 1 GO法操作符类型 Fig. 1 Type of GO methodology operators |
1) 逻辑操作符:此类操作符没有状态概率数据,仅代表一种逻辑运算规则.逻辑操作符包括第2、9、10、11、13、14、15类操作符.
2) 功能操作符:此类操作符包含自身状态值及运算逻辑.功能操作符包括第1、3、4、5、6、7、8、12、16、17类操作符.
其中,在工程中最常用的操作符类型为1、2、5、6、7、10、11.本文将针对这些常用操作符进行GO法可修系统的研究.
GO法应用于可修系统时,操作符代表的单元是可修系统,因此操作符的成功状态概率P(1)就是可修系统的可用度,操作符的故障状态概率P(2)就是可修系统的不可用度,同时其故障率和维修率分别为λ、μ[2].在工程系统中,λ和μ一般服从指数分布,其值为常数.
1.2 动态贝叶斯网络基本原理
动态贝叶斯网络是静态网络在时间上的一种扩展.它由初始网络和转移网络构成,将时间因素引入其中,使得贝叶斯网络随时间变化,数据发生相应的转移变化[15].整个网络含有有限个时间片段,每个时间段都有其对应的条件概率表(Conditional Probability Table,CPT).
如图 2所示为“与”逻辑关系对应的动态贝叶斯网络,A(T)、B(T)为其两个输入的初始网络;A(T+ΔT)、B(T+ΔT)为其转移网络,R(T)
为其初始网络的输出;R(T+ΔT)为其转移网络的输出.在动态贝叶斯网络分析中,通常只关注转移网络的输出,所以在以下的分析中,用简化图 2(b)来表示图 2(a)的动态贝叶斯网络.同时,根据“与”的逻辑关系,可得到相应的条件概率分布.
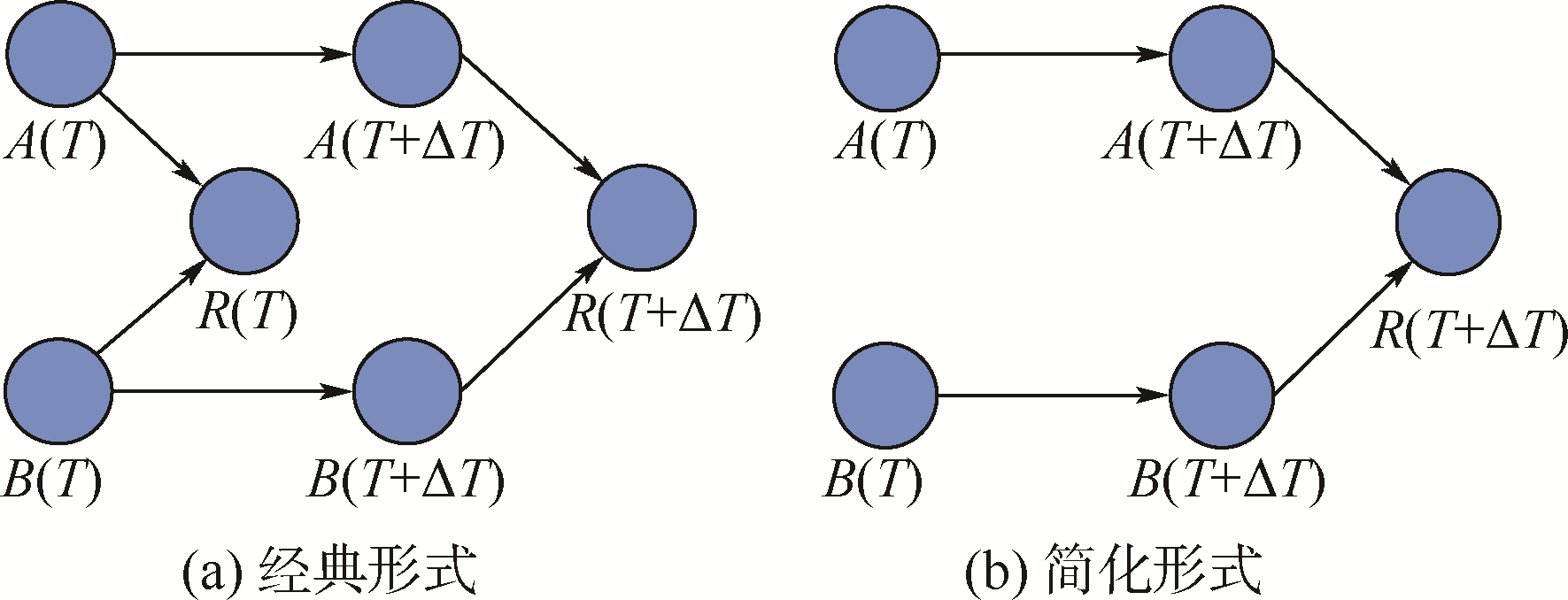 |
| 图 2 “与”逻辑对应的动态贝叶斯网络 Fig. 2 Dynamic Bayesian network of logic “AND” |
动态贝叶斯网络作为一种形式化方法,可以很好地描述系统中多状态、多时序等复杂特性,考虑基于动态贝叶斯网络来对GO法模型中的可修动态时序特性进行形式化映射,可以有效地结合两者的优势,为GO法模型的计算和应用提供一种新的途径[16, 17].
1.3 可修部件的动态贝叶斯网络建模
对于系统部件,其处于正常工作状态和故障状态的概率是随时间变化的,这种随时间变化的规律可以用动态贝叶斯网络来进行表达.如图 3所示为操作符对应的动态贝叶斯网络.在不可修的条件下,在(T+ΔT)时刻处于1状态的条件概率为
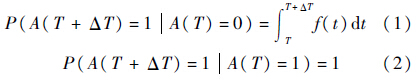
 |
| 图 3 操作符动态贝叶斯网络 Fig. 3 Dynamic Bayesian network of operator |
对于可修部件,只需将式(2)修改为[18]
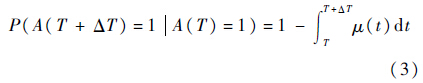
2 动态贝叶斯网络映射 2.1 操作符到动态贝叶斯网络的一般映射规则[19]
从操作符(包括输入信号、操作符本身和输出信号)到动态贝叶斯网络的转换过程的一般映射规则的具体步骤如下:
1) 将操作符(非逻辑门操作符)及其输入信号流映射为动态贝叶斯网络的初始网络根节点,并同时建立相应的各初始网络根节点的转移网络子节点,再建立初始网络中的父节点和转移网络中的对应子节点连接关系.
2) 将每一路输出信号流(除第5类操作符)映射为转移网络的一个节点,并建立与步骤1)中转移网络中的所有节点的父子关联关系(前者为子,后者为父).
3) 根据操作符的状态概率确定初始网络根节点的先验概率,并同时确定对应转移网络中子节点的条件概率表.
4) 根据操作符的运算逻辑给出所有输出信号流对应的转移网络子节点的条件概率表.
2.2 逻辑操作符的动态贝叶斯网络映射
在GO法中,第2、10、11类操作符分别对应或、与、M取K 3种逻辑关系,这3类操作符都有多路信号输入,一路信号输出.第2、10类操作符实际为M取K逻辑门的特例,在第2类操作符中K=1,在第10类操作符中K=M.因此只需给出第11类操作符的动态贝叶斯网络映射和计算过程即可.
如图 4所示为第11类操作符模拟3个输入信号的3取2逻辑元件,假设每个输入信号都仅有两种状态(1—正常,2—故障),根据第2.1节的映射规则,可以得到其相应节点的概率及子节点的条件概率表.
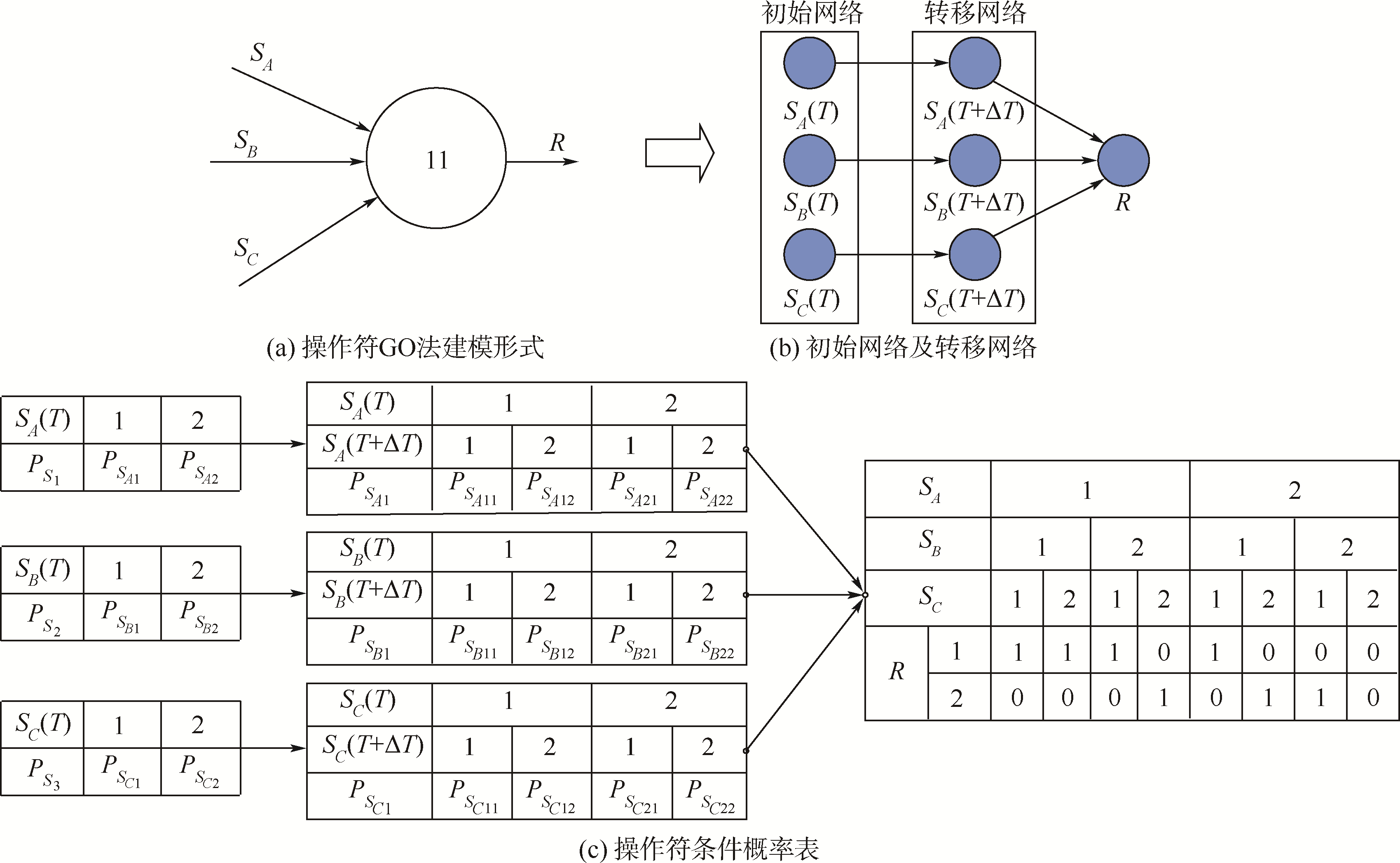 |
| 图 4 第11类操作符及对应动态贝叶斯网络 Fig. 4 Type 11 operator and its dynamic Bayesian network |
依据条件概率表,可以得出输出信号R的成功状态(1状态)的概率,具体计算过程如下:
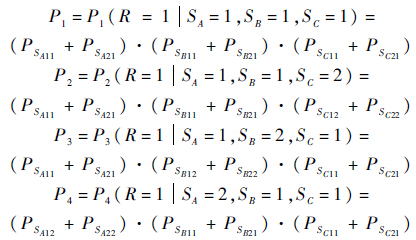

根据第1.3节中动态贝叶斯网络在可修操作符中的定量计算公式可知,式(4)中:
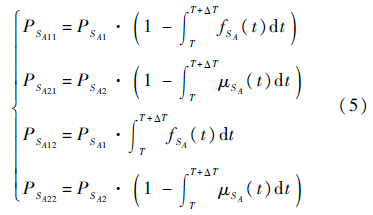
输入信号SB、SC的计算与SA相似,在此不做赘述.
2.3 功能操作符的动态贝叶斯网络映射
1) 第1、3、8类操作符.
第1、3、8类操作符均为工程上常用的操作符,这3类操作符均有一路输入信号,一路输出信号,但其本身状态数不同.本文以第1类操作符为例来说明此类操作符的映射和计算过程.
第1类操作符是最常用的操作符,其模拟只有两种状态的单元(成功,失败),一般用来模拟电阻、开关等设备.
根据第2.1节的映射规则,其相应节点的概率及子节点的条件概率表如图 5所示.输出信号的成功状态概率为
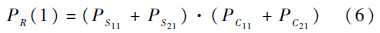
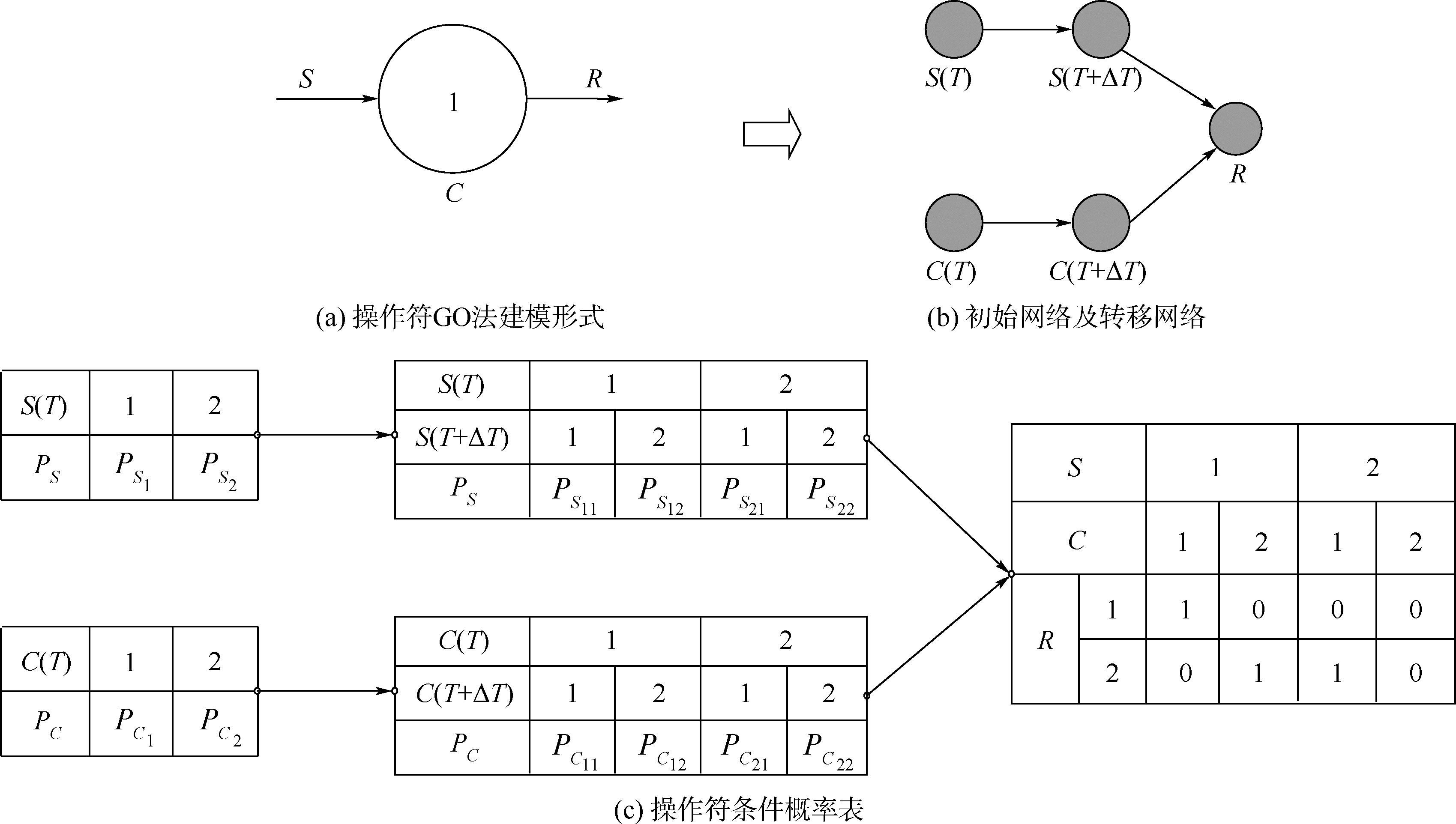 |
| 图 5 第1类操作符及对应动态贝叶斯网络 Fig. 5 Type 1 operator and its dynamic Bayesian network |
根据第1.3节可知,其中:
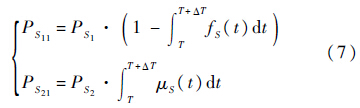
2) 第5类操作符.
第5类操作符是工程上最常用的输入操作符,一般作为建模系统的输入使用.根据第2.1节的映射规则,其相应节点的概率及子节点的条件概率表如图 6所示.
 |
| 图 6 第5类操作符及对应动态贝叶斯网络 Fig. 6 Type 5 operator and its dynamic Bayesian network |
依据条件概率表,可以给出第5类操作符输出信号的1状态概率:
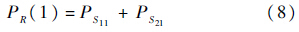
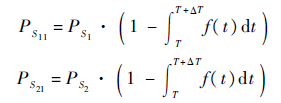
3) 第6、7类操作符.
第6、7类操作符模拟的是有两个输入信号一个输出信号的元件,其本身具有3种状态(状态值:0,1,2).第6类操作符在两个输入均正常时才有输出信号,一般用来模拟常开的接触器、未合上的电闸等.第7类操作符恰好相反,其在两个输入均正常时,输出信号被截断,一般用来模拟常闭的接触器、常开的流体阀门等.
根据第2.1节的映射规则,第6类操作符的GO法模型、对应的动态贝叶斯网络及条件概率表如图 7所示.依据条件概率表,操作符6的输出信号的成功状态概率的具体计算步骤为
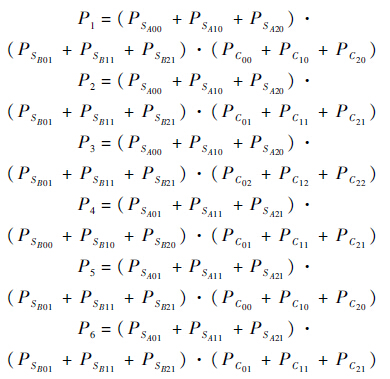
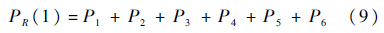
对于第7类操作符,只需要根据其逻辑修改图 7中的条件概率表即可,计算步骤与上述第6类操作符类似.
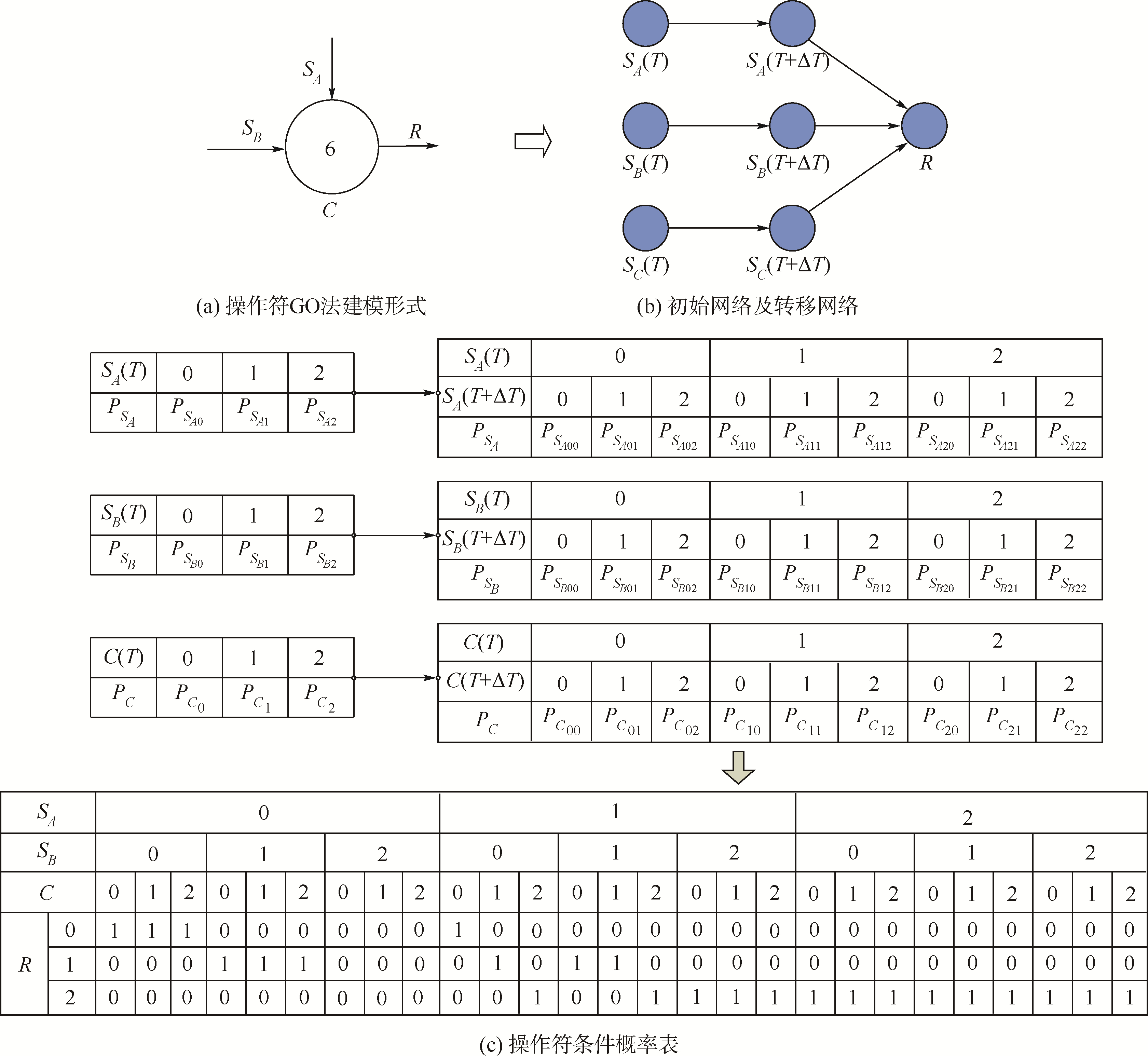 |
| 图 7 第6类操作符及对应动态贝叶斯网络 Fig. 7 Type 6 operator and its dynamic Bayesian network |
2.4 操作符相关性及其动态贝叶斯网络映射
在工程系统中,单元和单元之间往往不是相互独立的,在停工、备用、维修等方面存在相关性,相关性表现在以下方面[2, 18]:
1) 停工相关:可修系统由于某些单元的故障而停工维修时,没有发生故障的单元随系统的停工而停止工作,且不再发生故障.这种相关性定义为停工相关.
在工程中,停工相关一般表现为串联或与门形式,本文以串联为例,如图 8所示.系统的最终输出只有两种状态,状态0仅用来表现操作符的工作状态,所以通过计算可求得:PR(0)=0.在备用相关和维修相关中与上述情况相似,不再赘述.假设1-1、1-2均有3种状态(0—停工等待,1—正常,2—故障),其中状态0为停工相关中的中间状态,R为其串联输出.
 |
| 图 8 操作符之间的停工相关 Fig. 8 Shutdown dependence between operators |
2) 备用相关:假设冗余单元处于备用状态时不会发生故障或发生故障率较小,那么冗余备用单元发生故障就和其余单元是否处于故障状态有关,这种相关性定义为备用相关.
现假设备件系统中包含一个主部件1-1和一个备份部件1-2,且两个部件均为两状态单元.假设当部件1-1正常工作时,备件1-2处于备份状态,故障率为0.其GO法模型及其对应的动态贝叶斯网络如图 9所示.
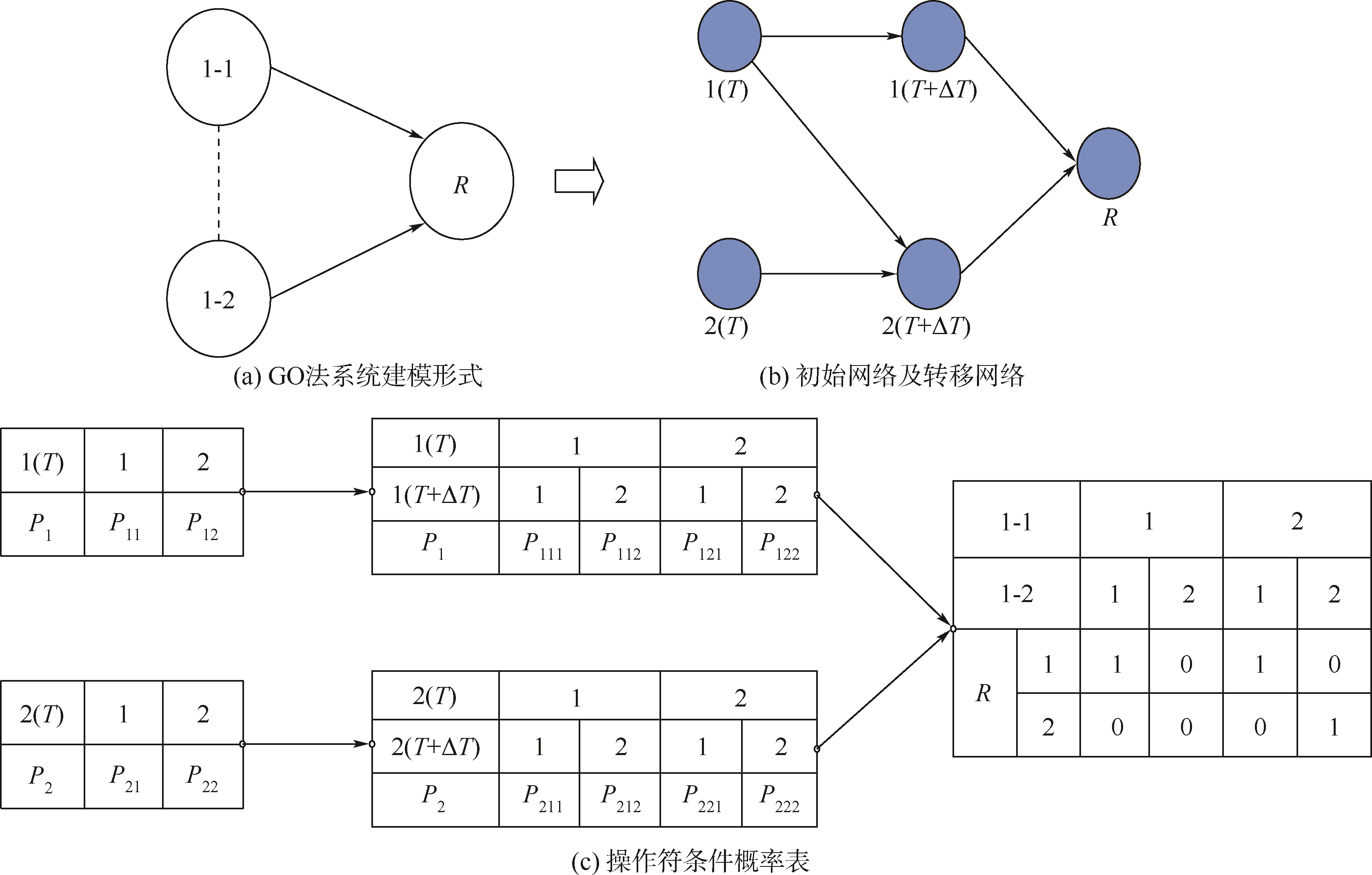 |
| 图 9 操作符之间的备用相关 Fig. 9 Standby dependence between operators |
根据图 9中的动态贝叶斯网络节点,则系统的故障概率为
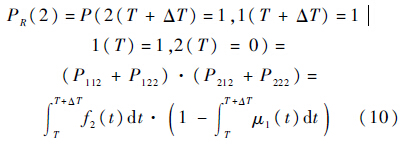
3) 维修相关:当可修系统有多个单元同时处于故障状态,而维修工不足,即有些单元在发生故障后不能及时维修.这种相关性定义为维修相关.
假设操作符1-1、1-2均有3种状态(0—等待维修,1—正常,2—维修),且维修工数为1,R为其输出.其GO法模型及其对应的动态贝叶斯网络如图 10所示.
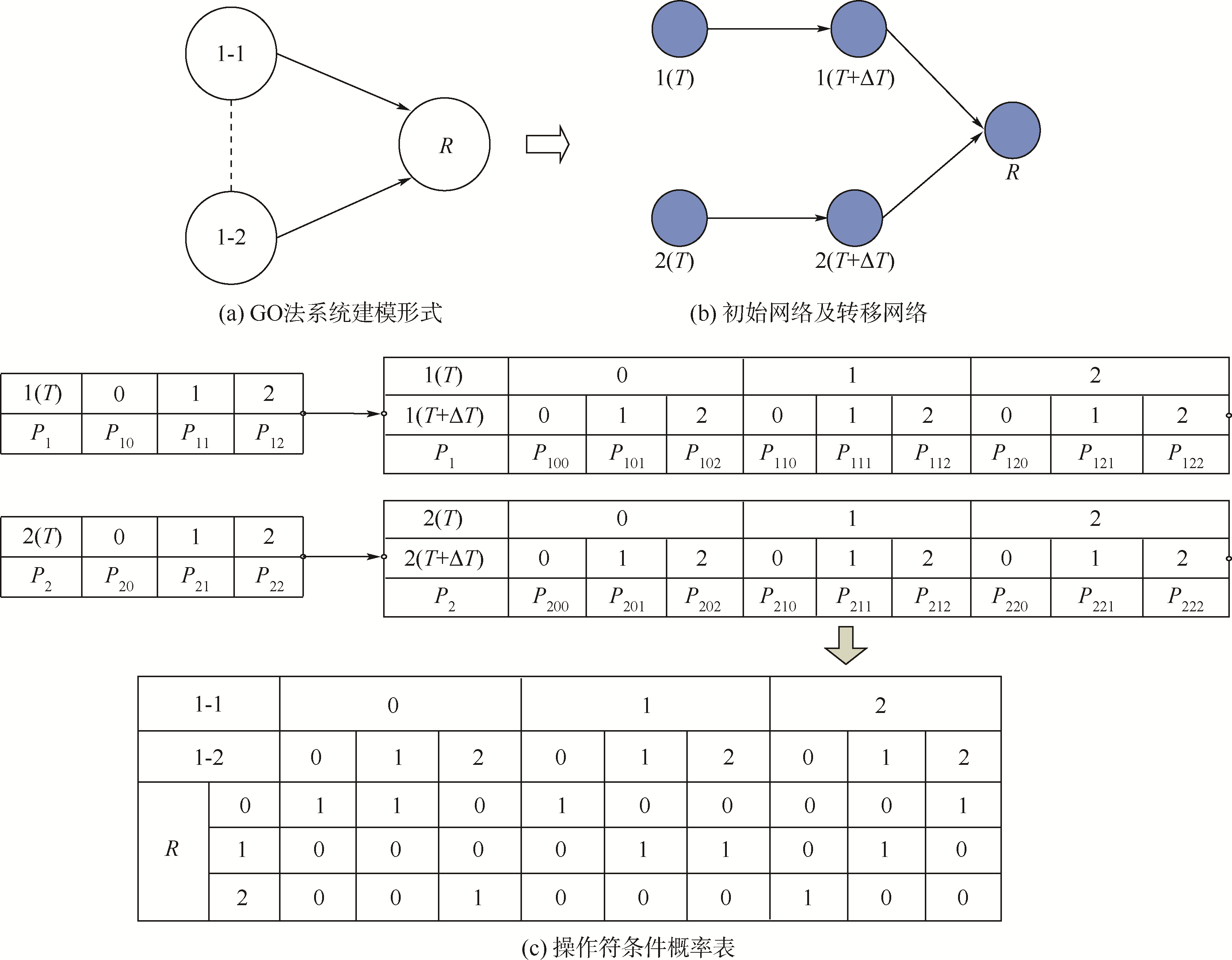 |
| 图 10 操作符之间的维修相关 Fig. 10 Repair dependence between operators |
根据图 10中的动态贝叶斯网络节点,则系统的故障概率为

3 案例验证
本节中通过核电站高压注水系统的实际案例来对算法的流程步骤进行详细的描述.随着传统资源的稀缺,新型能源逐渐成为了全球化的热点.核能源作为清洁、环保的新型能源已成为各国竞相开发的对象.而核电站中的高压注水系统是核电站中重要的安全系统之一其作用是向堆芯注入冷却剂,保持反应堆冷却剂的数量,维持堆芯继续冷却,使反应堆中的余热安全转移.
核电站高压注水系统由水箱经过主阀门分两路供水,第一路由3个隔离阀、3个上冲离心泵和3个逆止阀组成3条支路,经过隔离阀直接向核电站的主回路冷端注水.另一路由2个隔离阀、2个安全阀和2个逆止阀组成2条支路,通过隔离阀直接向核电站的主回路热端注水,同时也向主回路冷端注水.
如图 11所示是核电站高压注水系统的GO法建模图,其中的功能操作符均只有两种状态(1—成功,2—故障),要求计算冷端注入(信号流23)和热端注入(信号流22)的成功和故障概率.该GO图模型中,信号流2输出的第一路的3条支路是可修的,其余操作符均不考虑修复问题.且操作符18是3取2的冗余并联子系统,操作符19是2取1的冗余并联子系统,表 1列出了可修操作符的可靠性参数,表 2列出了不可修操作符的可靠性参数.
 |
| 图 11 核电站高压注水系统GO图 Fig. 11 High-pressure-water-infusion system GO graph of nuclear power station |
| 编号 | 类型 | 单元名称 | 故障率/a-1 | 平均维修时间/h |
| 3-5 | 1 | 隔离阀A-E | 0.21 | 8.0 |
| 8-10 | 1 | 上冲离心泵A-C | 2.80 | 8.0 |
| 13-15 | 1 | 逆止阀A-E | 0.08 | 8.0 |
| 注:故障率每年按8 760 h计算. | ||||
| 编号 | 类型 | 单元名称 | 故障率/a-1 | 平均维修时间/h |
| 1 | 5 | 水箱 | 0 | |
| 2 | 1 | 主阀门 | 0.38 | 8.0 |
| 6,7 | 1 | 隔离阀D-E | 0.21 | 8.0 |
| 11,12 | 1 | 安全阀A-B | 2.80 | 8.0 |
| 16,17 | 1 | 逆止阀D-E | 1.92 | 8.0 |
| 18 | 11 | 冗余3取2 | 0.08 | 8.0 |
| 19 | 2 | 或门 | ||
| 20,22 | 1 | 隔离阀F-H | 0.21 | 8.0 |
| 23 | 2 | 或门 |
根据第1.3节和第2.4节中的定量计算,首先对系统中的可修操作符进行动态贝叶斯转换,并对其进行计算,得到可修操作符的动态数据;然后对不可修操作符进行动态贝叶斯转换,最终将整个系统连接成动态贝叶斯网络.根据GO图的结构及其对应的动态贝叶斯网络,通过软件GeNIe2.0来建立动态贝叶斯网络,利用成熟的贝叶斯网络算法来最终求得系统的成功和失败概率,如图 12所示.
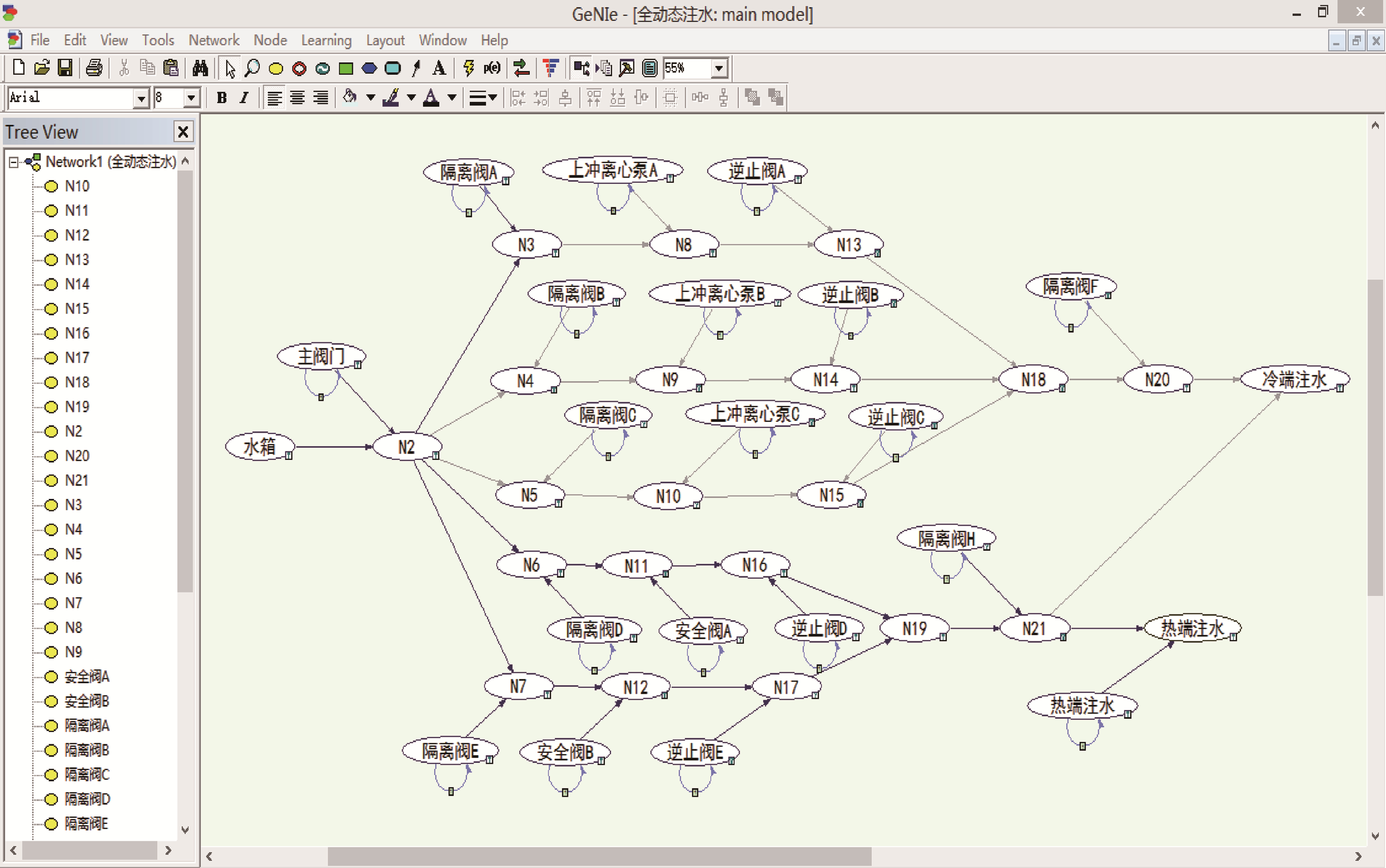 |
| 图 12 核电站高压注水系统动态贝叶斯网络转移图 Fig. 12 Dynamic Bayesian network transition diagram of high-pressure-water-infusion system of nuclear power station |
图 12中代表设备本身的节点向其本身发出的信号代表操作符本身的状态从初始网络转移到转移网络;其他节点均代表操作符的输入信号.
假设所有部件在初始状态均为正常工作状态,即在初始时刻t=0 h时,PR(1)=1,PR(2)=0.输入在t=1 h时设备节点的数据,如表 3所示.
| 操作符名称 | t=0 h | t=1 h | |
| PR(1) | PR(2) | ||
| 主阀门 | PR(1) | 0.999 957 | 0.000 043 |
| PR(2) | 0 | 1 | |
| 隔离阀D-E | PR(1) | 0.999 976 | 0.000 024 |
| PR(2) | 0 | 1 | |
| 安全阀A-B | PR(1) | 0.999 781 | 0.000 219 |
| PR(2) | 0 | 1 | |
| 逆止阀D-E | PR(1) | 0.999 990 | 0.000 010 |
| PR(2) | 0 | 1 | |
| 隔离阀F-H | PR(1) | 0.999 976 | 0.000 024 |
| PR(2) | 0 | 1 | |
| 隔离阀A-C | PR(1) | 0.999 976 | 0.000 024 |
| PR(2) | 0.882 5 | 0.117 5 | |
| 上冲离心泵A-C | PR(1) | 0.999 680 | 0.000 320 |
| PR(2) | 0.882 5 | 0.117 5 | |
| 逆止阀A-C | PR(1) | 0.999 99 | 0.000 01 |
| PR(2) | 0.882 5 | 0.117 5 | |
将表 3中的数据填入到软件中,最终计算出核电站高压注水系统冷端和热端的动态可用度如图 13所示,并且计算在t=500 h时系统输出的可靠性数据,如表 4所示.
| 系统可靠性参数 | 热端注水 | 冷端注水 |
| 工作概率 | 0.942 161 | 0.953 521 |
| 停工概率 | 0.057 839 | 0.046 479 |
| 故障率λ/10-4 | 0.433 90 | 0.683 66 |
| 平均工作时间MTBF/h | 23 046.6 | 14 627.1 |
由图 13可见,系统的可用度随着时间逐渐减低,且由于不可修操作符的存在,其在故障后无法进行修复,使得系统可用度无法最终达到一个稳态值.
 |
| 图 13 核电站高压注水系统动态可用度 Fig. 13 Dynamic availability of high-pressure-water-infusion system of nuclear power station |
4 结 论
本文提出了基于动态贝叶斯网络的GO法可修系统新算法,给出了基于动态贝叶斯网络的可修GO法定量计算公式,并对可修操作符的动态相关性进行了定量计算,最后通过核电站高压注水系统的案例来说明算法的应用流程,经验证表明:
1) 新算法无需考虑共有信号问题,可根据系统的组成结构直接将操作符转换成为动态贝叶斯网络模型.
2) 新算法可通过成熟的贝叶斯网络软件对可修复操作符直接进行定量求解.
3) 新算法计算简便且转换过程简单直观,易于理解,便于GO法在工程中的推广应用.
| [1] | Shen Z P, Gao J, Huang X R.A new quantification algorithm for the GO methodology[J].Reliability Engineering & System Safety, 2000, 67(3):241-247. |
| Click to display the text | |
| [2] |
沈祖培,黄祥瑞.GO法原理及应用:一种系统可靠性分析方法[M].北京:清华大学出版社, 2004:14-40. Shen Z P, Huang X R.Principle and application of GO methodology[M].Beijing:Tsinghua University Press, 2004:14-40(in Chinese). |
| [3] | Shen Z P, Wang Y, Huang X R.A quantification algorithm for a repairable system in the GO methodology[J].Reliability Engineering & System Safety, 2003, 80(3):293-298. |
| Click to display the text | |
| [4] | Weber P, Jouffe L.Reliability modelling with dynamic Bayesian network[C]//5th IFAC Symposium on Fault Detection Supervision and Safety of Technical Processes.Washington, D.C.:Elsevier Science, 2003. |
| Click to display the text | |
| [5] | Boudali H, Dugan J B.A new Bayesian network approach to solve dynamic fault trees[C]//51st Annual Reliability and Maintainability Symposium, RAMS 2005:The International Symposium on Product Quality and Integrity.Piscataway, NJ:IEEE Press, 2005:451-456. |
| Click to display the text | |
| [6] | Portinale L, Raiteri D C, Montani S.Supporting reliability engineers in exploiting the power of dynamic Bayesian networks[J].International Journal of Approximate Reasoning, 2009, 51(2):179-195. |
| Click to display the text | |
| [7] |
周忠宝,马超群,周经伦,等.基于动态贝叶斯网络的动态故障树分析[J].系统工程理论与实践, 2008, 2(2):35-42. Zhou Z B, Ma C Q, Zhou J L, et al.Dynamic fault tree analysis based on dynamic Bayesian networks[J].Systems Engineering-Theory & Practice, 2008, 2(2):35-42(in Chinese). |
| Cited By in Cnki (35) | |
| [8] |
苏傲雪,范明天,李仲来,等.基于动态贝叶斯网络的配电系统可靠性分析[J].华东电力, 2012, 11(11):1912-1915. Su A X, Fan M T, Li Z L, et al.Reliability analysis of distribution system based on dynamic Bayesian network[J].East China Electric Power, 2012, 11(11):1912-1915(in Chinese). |
| Cited By in Cnki (2) | |
| [9] |
姚成玉,陈东宁,王斌.基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J].机械工程学报, 2014, 50(2):193-201. Yao C Y, Chen D N, Wang B.Fuzzy reliability assessment method based on T-S fault tree and Bayesian network[J].Journal of Mechanical Engineering, 2014, 50(2):193-201(in Chinese). |
| Cited By in Cnki (14) | |
| [10] |
周忠宝,董豆豆,周经伦.贝叶斯网络在可靠性分析中的应用[J].系统工程理论与实践, 2006, 6(6):95-98. Zhou Z B, Dong D D, Zhou J L.Application of Bayesian networks in reliability analysis[J].Systems Engineering-Theory & Practice, 2006, 6(6):95-98(in Chinese). |
| Cited By in Cnki (14) | |
| [11] |
邓鑫洋,邓勇,章雅娟,等.一种信度马尔科夫模型及应用[J].自动化学报, 2012, 38(4):666-668. Deng X Y, Deng Y, Zhang Y J, et al.A belief Markov model and its application[J].Acta Automatica Sinica, 2012, 38(4):666-668(in Chinese). |
| Cited By in Cnki (19) | |
| [12] | Druzdzel M J.SMILE:Structural modeling, inference, and learning engine and GeNIe:A development environment for graphical decision-theoretic models[C]//Proceedings of the National Conference on Artificial Intelligence.Orlando, Florida:AAAI/IAAI, 1999:900-901. |
| Click to display the text | |
| [13] | Doguc O, Ramirez-Marquez J E.An automated method for estimating reliability of grid systems using Bayesian networks[J].Reliability Engineering & System Safety, 2012, 104(1):96-105. |
| Click to display the text | |
| [14] | Chu B B.GO methodology:Overview manual, EPRI NP-3123[R].Kansas City:Electric Power Research Institute, 1983:125-130. |
| [15] |
李海军.贝叶斯网络理论在装备故障诊断中的应用[M].北京:国防工业出版社, 2009:60-82. Li H J.Application of Bayesian network in fault diagnosis of military equipment[M].Beijing:National Defense Industry Press, 2009:60-82(in Chinese). |
| [16] | Mi J, Li Y, Huang H Z, et al.Reliability analysis of multi-state systems with common cause failure based on Bayesian networks[C]//Proceedings of 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering.Piscataway, NJ:IEEE Press, 2012:1117-1121. |
| Click to display the text | |
| [17] |
马德仲,周真,于晓洋,等.基于模糊概率的多状态贝叶斯网络可靠性分析[J].系统工程与电子技术, 2012, 34(12):2607-2611. Ma D Z, Zhou Z, Yu X Y, et al.Reliability analysis of multi-state Bayesian networks based on fuzzy probability[J].Systems Engineering and Electronics, 2012, 34(12):2607-2611(in Chinese). |
| Cited By in Cnki (11) | |
| [18] |
周忠宝.基于贝叶斯网络的概率安全评估方法及应用研究[D].长沙:国防科学技术大学, 2006. Zhou Z B.Research on methods and application of probabilistic safety assessment based on Bayesian networks[D].Changsha:National University of Defense Technology, 2006(in Chinese). |
| Cited By in Cnki (59) | |
| [19] |
刘林林,任翌,王自力,等.基于贝叶斯网络的GO法模型算法[J].系统工程与电子技术, 2015, 37(1):212-218. Liu L L, Ren Y, Wang Z L, et al.Algorithm based-on Bayesian networks for GO methodology[J].Systems Engineering and Electronics, 2015, 37(1):212-218(in Chinese). |
| Cited By in Cnki |



