2. 北京航空航天大学航空科学与工程学院, 北京 100191
2. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
物体间的接触、碰撞和摩擦现象是普遍存在的.如航天器的空中对接、飞机的着陆、步行机器人在地面上行走、机械手抓取工件以及具有非理想约束铰链(含间隙与摩擦)的机械系统运转等,都存在物体间的接触与分离、接触点的粘滞与滑移(stick-slip)等现象.如何描述物体间接触或碰撞时的相互作用力,如何给出粘滞(stick)与滑移判别的计算方法,是建立系统动力学方程并通过数值仿真分析其动力学行为的重要问题之一.
20世纪末和21世纪初,人们利用多种接触力模型研究物体的接触与碰撞问题,如Kelvin-Voigt接触力模型、Hertz接触力模型、Hunt-Crossley接触力模型和Lankarani-Nikravesh(L-N)接触力模型等[1].目前被广泛使用的摩擦模型有Coulomb干摩擦模型、修正的Coulomb摩擦模型、粘性摩擦模型、Stribeck摩擦模型[2]和Dahl摩擦模型[3]等,Coulomb摩擦模型被认为是较简单的摩擦模型[1, 4].
文献[5]利用修正的Kelvin模型研究了邻近的两个建筑物的碰撞问题.文献[6]利用L-N接触力模型研究了含间隙转动铰的速回机构的动力学建模与数值算法问题,并给出了接触点检测的数值方法,该文献未涉及摩擦问题.文献[7]利用L-N接触力模型、线弹性接触力模型和修正的Coulomb摩擦模型研究了含间隙滑移铰机械系统的动力学建模与数值算法问题,当滑移铰中的物块顶角与滑道碰撞时用L-N接触力模型,当物块的一个边(面)与滑道接触时用线弹性接触力模型.该文献采用修正的Coulomb摩擦模型无法反映物块与滑道间的stick-slip现象.文献[8, 9, 10]分别研究了具有含摩擦转动铰和滑移铰平面多刚体系统动力学的建模与数值算法问题,文献中均采用Coulomb干摩擦模型,应用试算法或线性互补方法有效地解决了stick-slip运动状态的切换问题,但无法反映铰链处的碰撞问题,当铰链的间隙不能忽略时,该方法则不适用.文献[11]研究了非对称库仑干摩擦模型对振动驱动机械系统动力学行为的影响,丰富了非光滑系统动力学.
本文基于非光滑动力学理论,给出了一种物体接触点含对称或非对称Coulomb干摩擦的平面运动刚体动力学的建模与数值计算方法.该方法是将研究对象视为刚体,考虑接触点的局部变形,将物体间的法向接触力表示成嵌入量与嵌入速度的函数;摩擦模型采用对称或非对称的Coulomb干摩擦模型;利用事件驱动法,将由于摩擦引起的stick-slip运动状态切换的判断问题以及处于粘滞(stick)状态时静摩擦力的计算问题转化成线性互补问题的求解.该方法与传统方法相比,不包含与接触-分离相关的互补量,因此线性互补方程的维数低,计算效率高,将适用于对称Coulomb干摩擦的互补算法推广到非对称Coulomb干摩擦模型.最后通过数值算例分析了非光滑平面运动刚体的动力学特性,并验证了该方法的有效性.
1 接触力学模型 1.1 法向接触力模型
当物体间接触或碰撞时,若考虑物体的局部变形,则一个物体会局部嵌入到另一个物体中,其法向嵌入量用δ表示,如图 1所示.用Hertz接触模型,法向接触力FN可表示[7]为

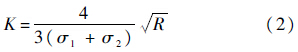
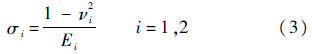
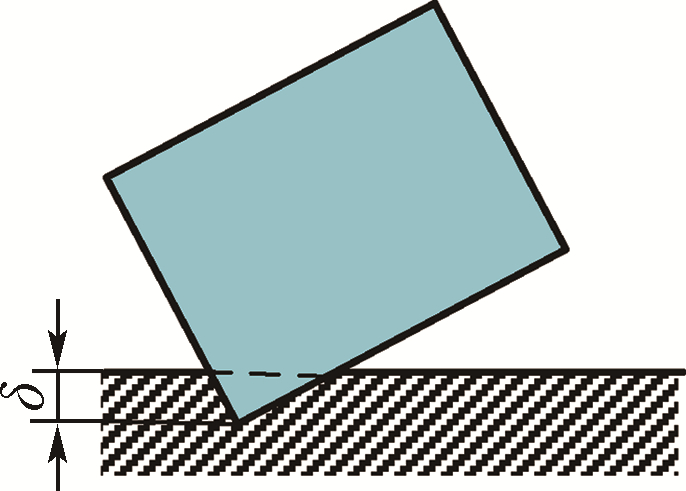 |
| 图 1 两物体间的接触模型 Fig. 1 Contact model between two bodies |
由于Hertz接触力模型中不含阻尼项,这与实际情况有一定的差距.文献[12]给出了一种非线性粘弹性接触力模型,其表达式为
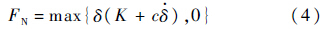

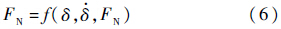
接触力模型的研究还在不断的深入和完善.
1.2 切向接触力模型
机械系统中常用的摩擦模型有多种[2, 3],其中Coulomb摩擦模型又可分为Coulomb干摩擦模型和修正的Coulomb摩擦模型,前者是相对速度的非连续函数(数值计算存在困难),后者是相对速度的连续函数(不易反映摩擦的静动态特性)[14].本文将采用非对称Coulomb干摩擦模型,该模型的数学表达式[11]为
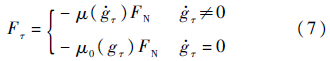

2 非光滑动力学方程及其数值求解算法 2.1 非光滑动力学方程
若设物体与固定面接触时,其接触面的法向量平行于y轴,用Newton-Euler方法可得平面运动刚体的动力学方程:
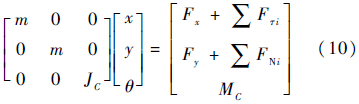
因为嵌入量和嵌入速度可以表示状态变量的函数,因此,从式(5)不难看出,法向接触力FNi是状态变量(x,y,θ,$\dot x$,$\dot y$,$\dot \theta $)的函数;由式(7)和式(8)可知,当$\dot g$τi≠0时,摩擦力Fτi也是状态变量的函数.根据状态变量可计算出FNi和Fτi.
但是,当$\dot g$τi=0时,摩擦力不仅与状态变量有关,还与广义加速度$\ddot x$、$\ddot y$、$\ddot \theta $有关.此时,方程式(10)等号右端的摩擦力也与广义加速度有关,这给数值求解带来了一定的困难.
2.2 Coulomb摩擦定律的互补关系
非光滑动力学方程数值计算的难点在于物体间接触点stick-slip状态切换的判断以及处于stick状态时摩擦力的计算.本文通过建立非对称Coulomb摩擦定律的互补关系,将上述计算问题转化为线性互补问题的求解.
当$\dot g$τi=0时,设对称的Coulomb干摩擦模型的静摩擦因数为μ0,则其正向摩擦余量和负向摩擦余量可定义为[14]
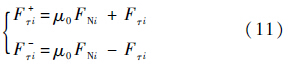
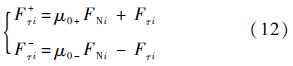

当$\dot g$τi=0时,接触点切向的正向加速度和负向加速度分别定义为[15]
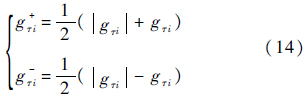

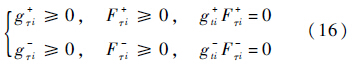
2.3 动力学方程的求解算法
物体接触点的切向速度可以表示为状态变量的函数,即$\dot g$τi=$\dot g$τi(q,$\dot q$),其中,q=[x y θ]T.
当$\dot g$τi≠0时,由式(7)和式(8)可知,摩擦力Fτi是q和$\dot q$的函数,动力学方程式(10)的右端均是q和$\dot q$的函数.因此,可直接应用常微分方程的数值计算方法求解该方程.
当$\dot g$τi=0时,由式(7)和式(9)可知,摩擦力Fτi不仅与q和$\dot q$有关,还与$\ddot q$有关.因此不能直接数值求解该方程.
将$\dot g$τi对时间求导可得
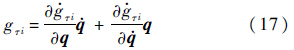
由式(13)、式(15)、式(17)和方程式(10)联立,可以得到线性互补方程:
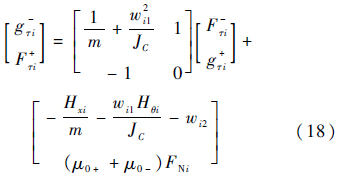
3 算 例 3.1 算例模型
设图 2所示箱体为均质体,其质量为m,边长分别是2a和2b,可与水平固定面发生接触和摩擦,图中C为箱体的质心,其坐标为(x,y),用本文给出的方法对其进行动力学仿真.
 |
| 图 2 算例中的箱体 Fig. 2 Slider in this example |
该箱体顶角1和顶角2的嵌入量可分别表示为
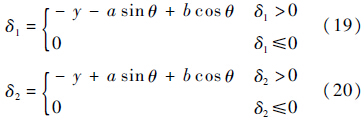
箱体顶角1和顶角2与固定面接触时的切向(沿x轴方向)速度可分别表示为
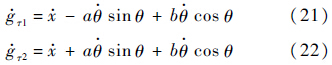
设系统参数为:m=2.0kg,a=0.4m,b=0.3m;接触力模型由式(5)给出,其中n=1.5,K=2.96×107N/m1.5,c=1.89×106N·s/m2.
3.2 数值仿真分析
算例1 箱体在重力作用下自由下落并与地面发生接触.设摩擦模型为对称的Coulomb干摩擦模型,其摩擦因数为μ+=μ-=0.3,μ0+=μ0-=0.4;初始条件为x0=0,y0=0.8m,θ0=π/6 rad,$\dot x$0=0,$\dot y$0=-3.0m/s,$\dot \theta $0=0.
图 3给出了箱体顶角1和顶角2的法向接触力FN1和FN2的时间历程图;图 4给出了δ1和δ2的时间历程图.由此可以看出,箱体的顶角2先与地面发生碰撞,其碰撞速度为4.96m/s,然后该点发生第二次碰撞,其碰撞速度为0.65m/s;随后顶角1与地面碰撞,其碰撞速度为3.16m/s;两个顶角经过几次碰撞后,箱体最终静止在地面上.由于碰撞速度不同,对应的碰撞冲击力的峰值也就不同.
 |
| 图 3 FN1和FN2的时间历程图 Fig. 3 Time history diagram of FN1 and FN2 |
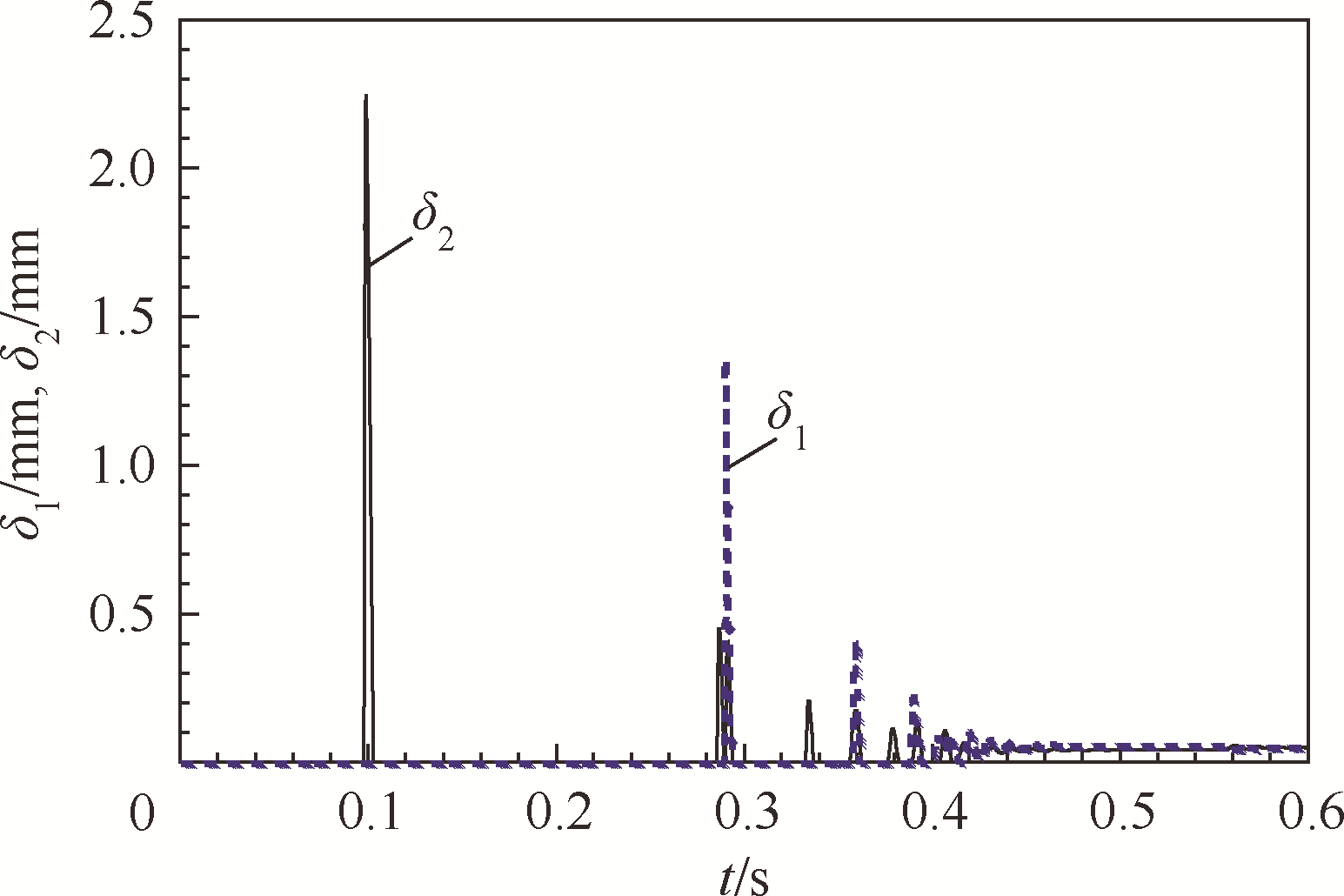 |
| 图 4 δ1和δ2的时间历程图 Fig. 4 Time history diagram of δ1 and δ2 |
图 5给出了x、y和θ的时间历程图,其运动状态与箱体受力状态吻合.图 6给出了箱体质心速度$\dot x $以及箱体所受摩擦力的时间历程图.由于箱体顶角2前两次与地面发生碰撞时,有向左的相对运动,因此摩擦力的方向向右,在其作用下,物体的质心有向右的速度.当箱体与地面再次发生碰撞时,由于运动速度向右,因此摩擦力向左.经过几次碰撞后,最终物体相对地面静止.
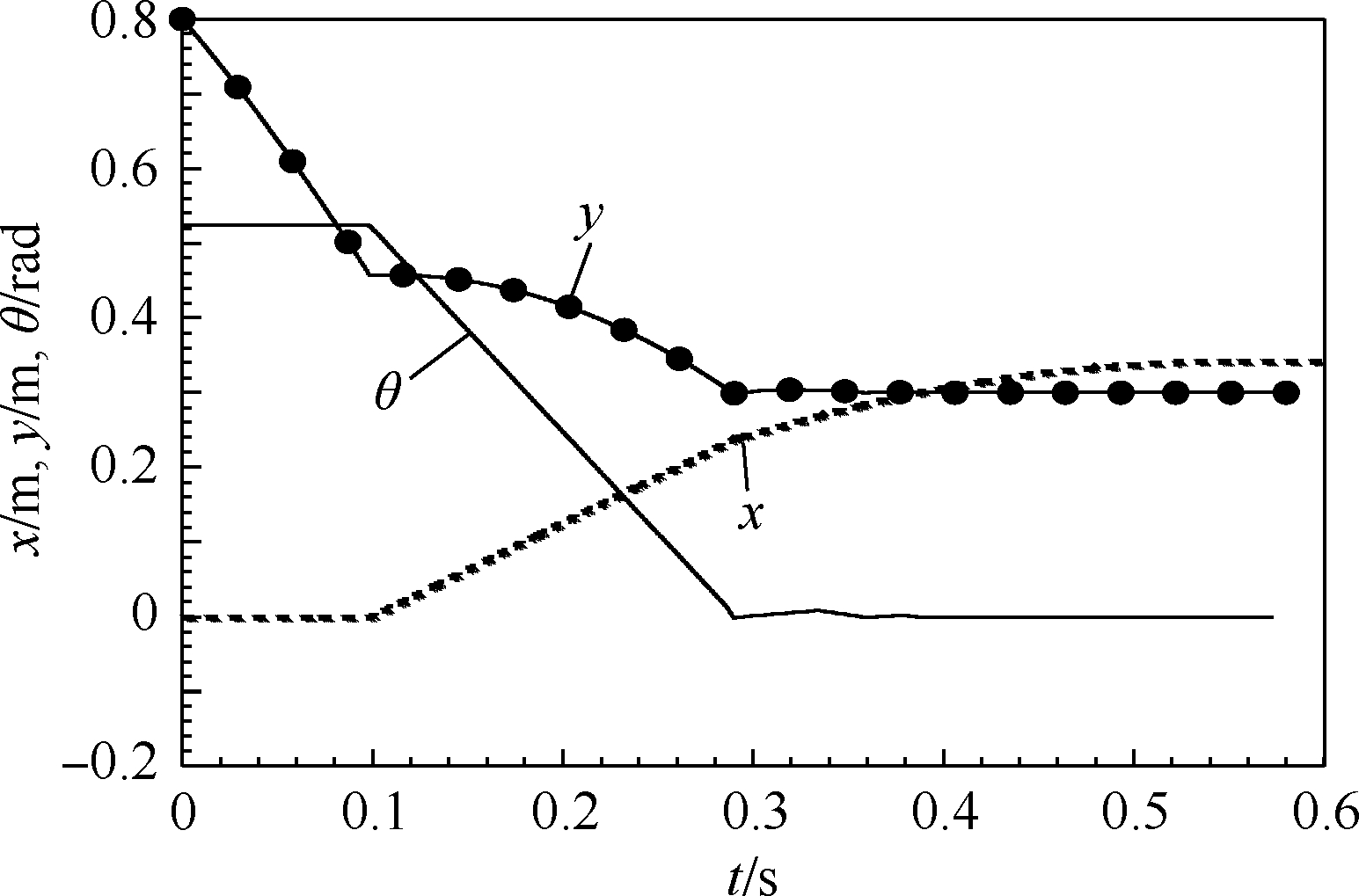 |
| 图 5 x、y和θ的时间历程图 Fig. 5 Time history diagram of x、y and θ |
 |
| 图 6 x·和Fτ的时间历程图 Fig. 6 Time history diagram of $\dot x $ and Fτ |
算例2 箱体放在水平地面上,其上作用一个水平力Fx=Asint.设摩擦因数为μ+=0.3,μ-=0.4,μ0+=0.5,μ0-=0.6,初始条件为x0=0,y0=b,θ0=0,$\dot x $0=$\dot y $0=0,$\dot \theta $0=0.
图 7给出了不同外激励幅值时,x和$\dot x $的时间历程图.当A=11N时,箱体有单向的速度且有stick-slip现象(见图 7(a));当A=12N时,箱体有双向速度且有stick-slip现象(见图 7(b));当A=18N时,箱体有双向的速度但无stick-slip现象(见图 7(c)).
 |
| 图 7 当A=11,12,18N时x和$\dot x $的时间历程图 Fig. 7 Time history diagram of x and $\dot x $ with A=11,12,18N |
算例1和算例2均用试算法进行了验证,试算法与本文给出的算法所得数值结果完全吻合.
4 结 论
基于非光滑动力学方法,利用线性互补理论,给出了一种含非对称Coulomb干摩擦的平面运动刚体动力学的数值算法.
1) 将物体间的法向接触力表示成物体间嵌入量和嵌入速度的函数,无需引入互补量,更易于分析物体间的接触与分离.
2) 建立了非对称摩擦余量互补关系,将原适用于含对称Coulomb干摩擦的LCP算法推广到非对称Coulomb干摩擦系统,使其具有更广泛的适用性.
3) 数值仿真算例表明,该算法易于分析非光滑系统中物体间的接触与分离和stick-slip现象.
| [1] | Flores P, Ambrósio J.Kinematics and dynamics of multibody systems with imperfect joints[M].Berlin:Springer, 2008:47-66. |
| [2] |
刘丽兰,刘宏昭,吴子英,等.机械系统中摩擦模型的研究进展[J].力学进展, 2008, 38(2):200-213. Liu L L, Liu H Z, Wu Z Y, et al.An overview of friction models in mechanical systems[J].Advances in Mechanics, 2008, 38(2):200-213(in Chinese). |
| Cited By in Cnki (165) | |
| [3] | Pennestri E, Valentini P P, Vita L.Multibody dynamics simulation of planar linkages with Dahl friction[J].Multibody System Dynamics, 2007, 17(4):321-347. |
| Click to display the text | |
| [4] | Pfeiffer F, Glocker C.Multibody dynamics with unilateral contacts[M].New York:John Wiley & Sons, Inc, 1996:70-91. |
| [5] | Ye K, Li L, Zhu H P.A modified Kelvin impact model for pounding simulation of base-isolated building with adjacent structures[J].Earthquake Engineering and Engineering Vibration, 2009, 8(3):433-446. |
| Click to display the text | |
| [6] | Flores P, Ambrósio J.On the contact detection for contact-impact analysis in multibody systems[J].Multibody System Dynamics, 2010, 24(1):103-122. |
| Click to display the text | |
| [7] | Flores P, Ambrosio J.Translational joints with clearance in rigid multibody systems[J].ASME Journal of Computational and Nonlinear Dynamics, 2008, 3(1):011007. |
| Click to display the text | |
| [8] |
庄方方,王琪.含摩擦柱铰链平面多体系统动力学的建模和数值方法[J].工程力学, 2012, 29(5):193-199. Zhuang F F, Wang Q. Modeling and numerical algorithm for planar multibody system with friction on revolute joints[J].Engineering Mechanics, 2012, 29(5):193-199(in Chinses). |
| Cited By in Cnki (3) | |
| [9] | Wang Q, Peng H L, Zhuang F F.A constraint-stabilized method for multibody dynamics with friction-affected translational joints based on HLCP[J].Discrete and Continuous Dynamical Systems Series B, 2011, 16(2):589-605. |
| Click to display the text | |
| [10] | Zhuang F F, Wang Q.Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints[J].Multibody System Dynamics, 2013, 29(4):403-423. |
| Click to display the text | |
| [11] | Fang H B, Xu J.Dynamics of a three-module vibration-driven system with non-symmetric Coulomb's dry friction[J].Multibody System Dynamics, 2012, 27(4):455-485. |
| Click to display the text | |
| [12] | Kisu L.A short note for numerical analysis of dynamic contact considering impact and a very stiff spring-damper constraint on the contact point[J].Multibody System Dynamics, 2011, 26(4):425-439. |
| Click to display the text | |
| [13] |
刘才山,陈滨,王玉玲.考虑摩擦作用的多柔体系统点-面碰撞模型[J].中国机械工程, 2000, 11(6):616-619. Liu C S, Chen B, Wang Y L.The point-surface impact model considering the friction effect in flexible multi-body system[J].China Mechanical Engineering, 2000, 11(6):616-619(in Chinses). |
| Cited By in Cnki (15) | |
| [14] |
王琪,庄方方,郭易圆.非光滑多体系统动力学数值算法的研究进展[J].力学进展, 2013, 43(1):101-111. Wang Q, Zhuang F F, Guo Y Y.Advances in the research on the numerical method fir non-smooth dynamics of multibody systems[J].Advances in Mechanics, 2013, 43(1):101-111(in Chinese). |
| Cited By in Cnki (3) | |
| [15] | Pfeiffer F, Foerg M, Uibrich H.Numerical aspects of non-smooth multibody dynamics[J].Computer Methods in Applied Mechanics and Engineering, 2006, 195(50):6891-6908. |
| Click to display the text |



