再入制导是指通过在线产生指令引导具有一定升力能力的再入飞行器从当前状态安全到达指定终端状态的过程[1].再入制导的核心是通过有效控制耗散能量,并满足过程物理约束和终端状态约束.飞行器一般为无动力再入,必须一次成功;同时要求制导律能够适应初始再入状态、气动、风场等方面的不确定性及可能的任务改变、终止或控制能力减弱的情形.
再入制导中的一类重要算法是轨迹跟踪制导,包括参考轨迹设计和轨迹跟踪两部分.制导律通过比较当前状态和参考轨迹之间的偏差产生迎角和倾侧角指令.轨迹跟踪制导以航天飞机的再入制导律为典型代表[2].航天飞机制导律设计包括参考阻力加速度剖面设计和在线的参考剖面跟踪.规划阻力参考剖面时主要考虑到纵程要求和满足过程约束.但实际上在规划时往往耗时耗力,参数需要反复试凑,在实际飞行和地面任务设计相差较大时,飞行器甚至可能无法安全返回.
为了提高再入制导的自主性和适应性,近年来专家学者们提出了多种再入参考轨迹的在线生成方法.文献[3]利用“拟平衡滑翔条件”将过程约束转换为对速度滚转角的约束,将非线性轨迹规划问题转化为顺序进行两次单参数搜索问题,能够快速生成满足所有约束条件的三自由度轨迹.文献[4]研究了最优阻力加速度剖面的在线生成方法,避免了地面的离线规划.文献[5]提出了在阻力加速度剖面规划参考轨迹,同时考虑到纵程和横程要求的轨迹快速生成算法.一旦在线参考轨迹生成,需要研究如何实现对参考轨迹的精确跟踪.应用于航天飞机阻力剖面跟踪的反馈线性化方法是轨迹跟踪的基准控制算法.文献[6]给出了一种近似反馈线性化方法,对三维轨迹的跟踪转换为对横程和纵程的跟踪,但仅对无拉偏的理想情况做了分析;反馈线性化方法在模型存在较大不确定性时(如验证飞行时),非线性项无法进行精确对消,控制性能将变差甚至可能失稳.线性二次型调节器(Linear Quadratic Regulator,LQR)控制由于反馈增益可以采用误差状态的线性反馈控制律构成最优闭环,设计时能够考虑允许的状态偏差和控制量偏差等多个指标,在参数不确定的情况下闭环系统也具有一定鲁棒性,在多入多出系统的控制方面获得了较多应用.文献[7]指出,基于LQR方法计算得到的反馈增益对于同一飞行器能够适用于不同再入参考轨迹的跟踪,且对初始条件的拉偏具有较好的鲁棒性;离线生成的最优增益具有在线应用于轨迹跟踪的潜力.但文献同时指出,LQR控制效果和精度依赖于参考轨迹特性,特别当轨迹倾角较陡时,跟踪精度将明显降低.文献[8]提出了一种封闭形式的近似滚动时域控制(Receding Horizon Control,RHC)方法,避免了在线积分和显式的增益调度;相比LQR方法,滚动时域控制对权重矩阵参数的选取较不敏感;方法能够实现三维轨迹的精确跟踪并能理论上保证闭环稳定性,但预测步长较多时计算量稍大.
轨迹线性化控制(Trajectory Linearization Control,TLC)方法是一种基于微分代数谱理论的非线性控制方法,在NASA先进制导控制项目中被成功应用于X-33的上升段姿控系统设计[9].本文将TLC方法在升力体飞行器设计中的应用从姿态回路扩展到制导回路,并结合利用“拟平衡滑翔条件”的在线轨迹生成算法[3],提出了一种基于TLC理论的再入轨迹跟踪制导律.TLC方法利用再入飞行器固有时间尺度分离的特点,将控制变量进行有效降阶,在高度环路和速度环路分别利用闭环谱配置对跟踪误差进行镇定,并能保证指数稳定性.新制导律通过与基于LQR和近似滚动时域控制的制导方法进行比较并经过三自由度蒙特卡罗拉偏仿真进行验证,证明了其有效性.
1 制导问题描述 1.1 再入动力学方程
滑翔再入飞行器相对旋转正地球的三自由度无量纲质点动力学方程[10]为
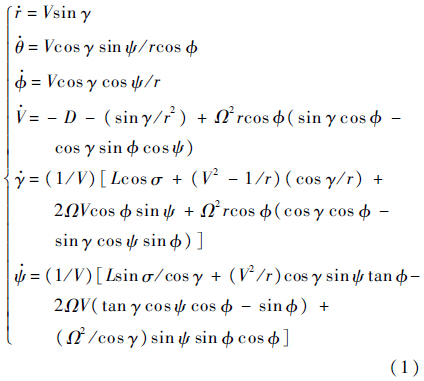
1.2 再入轨迹约束条件
再入轨迹需要满足的约束包括过程约束和终端约束.常见的过程约束包括热流$\dot Q$、动压q和法向过载约束nz,

距着陆场一段距离时飞行器将进入末端能量管理段(Terminal Area Energy Management,TAEM).再入段和TAME段在交接班时需满足一定的终端约束,包括高度约束rf、速度约束vf、航程约束sf和倾侧角约束σf,

1.3 飞行器模型
通用航空飞行器(Common Aero Vehicle-H,CAV-H)[11]是一种亚轨道升力体式再入飞行器,最大升阻比约为3.5.CAV-H由于升阻较大,机动能力强,能够实现较高的落点精度,且能从多种武器平台发射,因而和Hypersonic Technology Vehicle-2(HTV-2)一样作为美国未来实现全球打击的战略武器.本文以CAV-H模型为对象进行再入段设计.
1.4 参考轨迹分析
文献[3]将再入轨迹设计分为3段(如图 1所示):初始下降段、拟平衡滑翔段和Pre-TAEM段.初始下降段的主要作用是通过轨迹积分预测,引导飞行器进入再入走廊并保证与拟平衡滑翔段光滑衔接.拟平衡滑翔段是再入飞行的主要阶段,这一阶段的特点是轨迹倾角较小(<-1°)且变化较慢.对于低升阻比飞行器如X-33和X-38,再入飞行末段即Pre-TAEM段,这一段升力不足以维持平缓的滑翔飞行,轨迹倾角变化较为剧烈.对于高升阻比飞行器如航天飞机,文献[3]提出的“拟平衡滑翔条件”直到再入末端仍然可以较好满足,可以不再划分Pre-TAEM段.基于文献[3]提出的算法生成的参考轨迹可以满足第1.2节给出的动力学方程组(式(1))和所有轨迹约束条件.
 |
| 图 1 再入轨迹的构成 Fig. 1 Composition of entry trajectory |
本文研究针对实现以Pre-TAEM状态为终端条件的拟平衡滑翔段纵向参考轨迹的精确跟踪.在参考轨迹跟踪时,将倾侧角作为主要控制量;考虑到配平要求和热流限制,迎角剖面预先给定为某一随马赫数变化的函数,并对偏离给定迎角剖面的最大值给出限制.
2 轨迹跟踪制导律设计 2.1 TLC理论
TLC(其概念如图 2所示)结构由两部分组成:通过非线性模型伪逆求得给定标称输出η-(t)对应的标称控制量$\bar \mu $(t),以粗略对消系统的非线性,并将一般的轨迹跟踪问题转化为在误差坐标系的状态调节问题,上方带“-”的变量为变量的标称值;将非线性时变误差动力学方程组线性化,通过李雅普诺夫坐标变换将一般的线性时变方程组转化为线性时变系统标准型,并通过配置Parallel Differential Spectrum(PD谱)对误差动态进行镇定.反馈控制项$\tilde \mu $(t)由时变镇定控制器产生,并可写为状态误差量的线性反馈形式$\tilde \mu $(t)=K(t)$\tilde \xi $(t).上方带“~”的变量为变量的状态误差量.非线性模型中的ξ(t)、μ(t)、η(t)和θ(t)分别为状态、输入、输出和时变参数向量.f(·)和g(·)为非线性向量函数.关于非线性伪逆和PD谱配置的理论见文献[12].
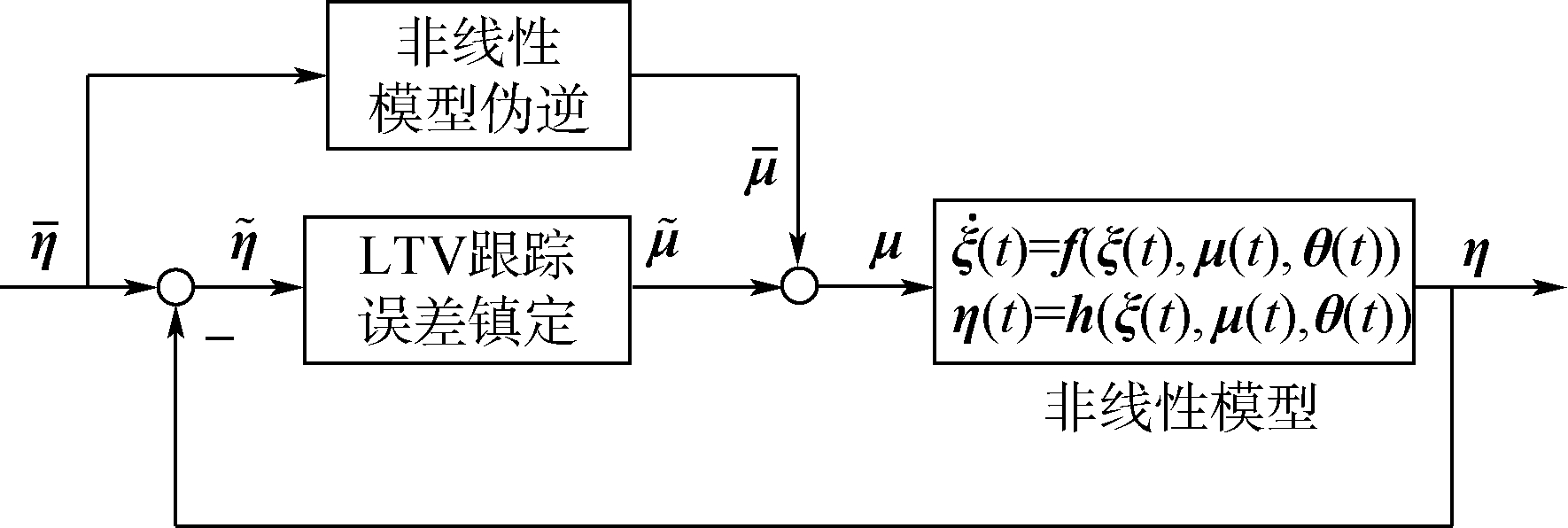 |
| 图 2 TLC概念图 Fig. 2 Conceptual configuration of TLC |
TLC对跟踪误差信号可以保证指数稳定性,闭环系统对正则扰动及奇异摄动都有很好的适应性.
2.2 环路划分和独立变量的选取
飞行器动力学不同状态变量在时间尺度上存在明显差异这一事实在航空航天领域被广泛应用于轨迹优化、控制律设计和系统分析中[13, 14, 15].利用时间尺度分离的特性,控制设计展现出的优势是可以减小控制变量个数并避免积分时由于不同变量变化速率不同带来的刚性数值问题.
TLC的控制策略是基于奇异摄动理论中的时间尺度分离思想,将全量、刚体的飞行器动力学模型分为2个回路,即制导回路(其TLC结构如图 3所示,带角标C的变量为环路的控制输出)和姿态回路;4个环路,对应高度(极慢动态)、速度(慢动态)、姿态角(较慢动态)和姿态角速率(快动态)环路,分别进行设计.本文分析仅涉及包含高度、速度环路的制导回路设计.
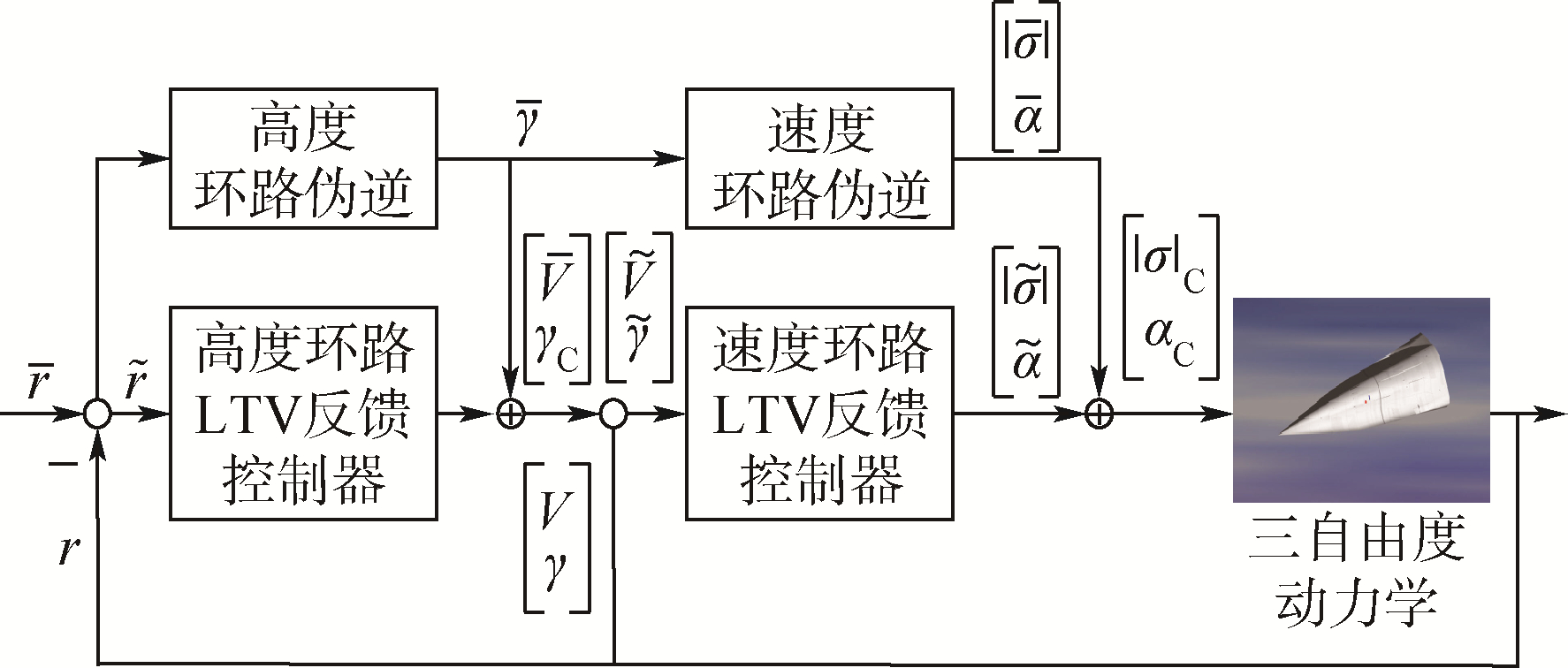 |
| 图 3 制导回路TLC结构图 Fig. 3 Configuration of TLC in guidance loop |
在轨迹跟踪制导中,当独立变量从与状态无关的时间变为与状态相关的单调变量时可以减小状态方程维数并增加控制的鲁棒性[7].两个可取的与时间相关的单调变量为能量e和已飞地球大圆距离sTravel(即为已飞航程).本文选取sTravel为独立变量,认为轨迹在线生成后储存为以sTravel为独立变量的数表;能量为独立变量时的控制器设计是相似的.
2.3 高度环路设计
在高度环路,轨迹倾角相对于高度变化是快动态,故将轨迹倾角取作高度控制的虚拟控制量.由于参考轨迹中包含了满足纵向动力学约束的轨迹倾角信息,故可直接从参考轨迹中取得高度环路的标称控制量$\bar \gamma $.为了改善稳态性能和提高对模型不确定性和扰动的鲁棒性,采用比例积分控制,
状态变量及其标称值分别为:${x_1} = {\left[ {\int {rds,r} } \right]^{\rm{T}}},{\bar x_1} = {\left[ {\int {\bar rds,\bar r} } \right]^{\rm{T}}}$.反馈控制量为$\tilde \gamma $,标称值为$\bar \gamma $.定义状态误差量${\tilde x_1} = {x_1} - {\bar x_1}$·sTravel为独立变量,对状态的积分和求导都应对sTravel进行.sTravel对时间的导数为
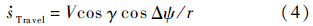
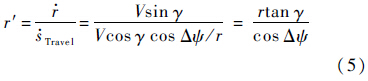
状态误差量的线性化方程为
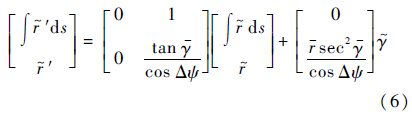
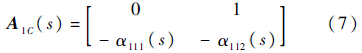
反馈控制量$\tilde \gamma (s) = {K_1}(s){\left[ {\int {\tilde rds,\tilde r} } \right]^{\rm{T}}}$,其中:
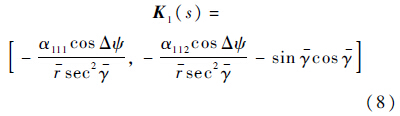
2.4 速度环路设计
速度环路迎角和倾侧角相对速度和弹道倾角的变化是快动态,因而作为速度和弹道倾角跟踪的控制量.与高度环路相同,标称迎角$\bar \alpha $和倾侧角指令$\bar \sigma $同样可直接从参考轨迹中取得.采用比例积分控制,系统状态变量及其标称值分别为
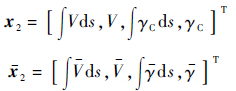
状态误差量为
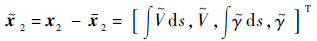
由于迎角对速度的控制效果较显著,倾侧角控制只影响轨迹倾角,故解耦后用迎角控制速度,倾侧角控制轨迹倾角.反馈控制量及其标称值分别为:$\tilde \mu $2=[|$\tilde \sigma $|,$\tilde \alpha $]T,$\bar \mu $2=[|$\bar \sigma $|,$\bar \alpha $]T,线性化方程为
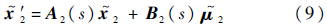
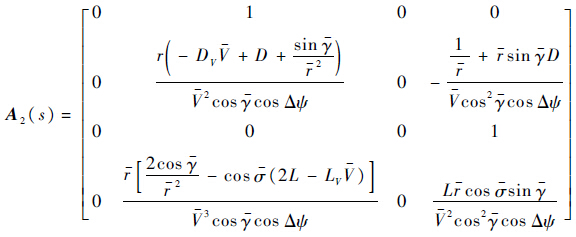
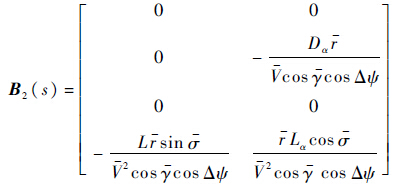
期望配置的闭环动态误差为
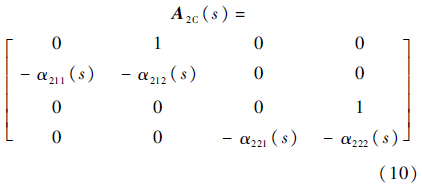

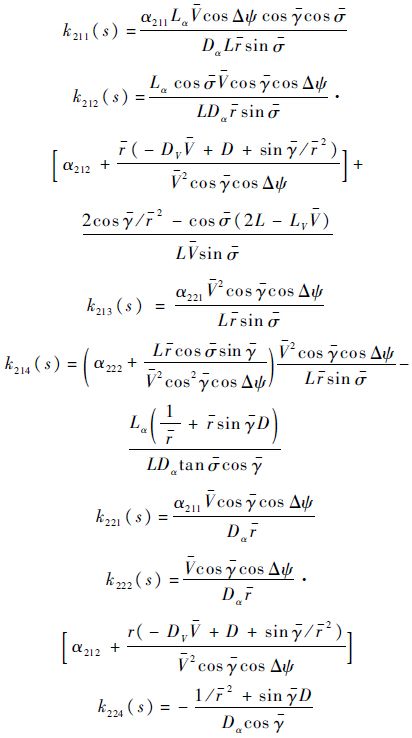
速度环路的控制输出为μ2C(s)=$\bar \mu $2(s)+$\tilde \mu $2(s).纵向制导确定了迎角的值和倾侧角的大小,倾侧角的符号将由侧向制导逻辑确定.
注意到当标称倾侧角为零,不能满足PD谱配置关于控制矩阵必须列满秩的条件[9].但在基于“拟平衡滑翔条件”的在线轨迹设计中,为防止倾侧角控制饱和,沿轨迹的标称倾侧角都不接近于零(文献[9]中图 8虚线),因此使用基于TLC的跟踪制导律不存在障碍.
3 控制器参数设置与调整
两环路配置的闭环动态矩阵中的参数αijl(s),i=1,2,j=1,2,l=1,2是通过闭环二阶PD谱得到

二阶PD谱阻尼和自然频率的意义可以参考二阶线性定常系统:阻尼比决定超调量,自然频率决定响应速度、控制用量和有限时间内的控制精度,参数和控制响应有直接对应关系.阻尼比调参可从二阶系统最佳阻尼比0.7开始,并根据实际时域响应情况适当增大阻尼比.对于以时间为自变量跟踪的制导律,速度环路的自然频率可以取为姿态角环路频率的1/5~1/3;高度环路也取为速度环路频率的1/5~1/3;环路自然频率初值的选取可参考飞行器本体长短周期的模态频率.
随着距目标点距离的减小,速度减小,对飞行器高度和速度控制精度的要求提高;而在再入中间过程中又不希望过短的调节时间要求导致翻转过程中倾侧角的超调过大.为更好兼顾过程飞行和终端约束的要求,两环路自然频率取为无量纲速度的线性函数形式(见表 1).
| 高度环路 | 速度环路 |
| ξ11=1.4 ωn11=6.5-5.0×$\bar V$ |
ξ21=1.4 ωn21=32.0-25.0×$\bar V$ ξ22=1.4 ωn22=10.0 |
4 仿真验证
这里用LQR方法和滚动时域控制作为基准控制方法与TLC的控制效果进行比较.LQR方法和滚动时域控制方法所用小扰动方程也是以sTravel为自变量线性化得到的.LQR方法用迎角、倾侧角跟踪高度、轨迹倾角和速度.
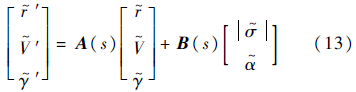
LQR权重矩阵按文献[7]中的偏差量原则选取,其中Q=diag[4×109,2.5×106,3.28×105],R=diag[3.28×103,25].滚动时域控制用迎角和倾侧角镇定高度和速度偏差,权重矩阵取为Q′=diag[1,1],R′=diag[100,0.1].初始再入时步长取h=0.006,线性过渡到再入末端时的h=0.0045,步数N=7.侧向制导律使用航向角误差漏斗逻辑[2].为更好地对比不同控制方法高度和速度跟踪精度,仿真截止条件取为2300m/s的Pre-TAEM速度对应的sTravel(这里统一取为距离TAEM300km),并要求飞行器大致指向目标.
三自由度拉偏仿真的设置条件见表 2,但为了统一仿真终端的参考高度和速度,对比三种控制方法时未对再入初始条件进行拉偏,使用相同的参考轨迹.为了更好显示不同控制方法终端速度-高度的分布情况,分别选取了前40条弹道的打靶结果显示在图 4中,靶心为2281m/s,35.51km.这里滚动时域控制高度跟踪稍差于LQR方法,但速度控制略优于LQR方法,两种控制方法效果整体相当;TLC方法的速度和高度落点更集中,略优于其他两种控制方法的精度.图 5~图 8是加入了初始条件拉偏后的TLC方法对参考轨迹的跟踪情况.可以看到,TLC方法对于不同参考轨迹也能实现精确跟踪.
| 拉偏项目 | 拉偏范围 |
| 水平风拉偏/(°) | [0,360]10%概率风 |
| 密度拉偏/% | [-10,10] |
| 阻力拉偏/% | [-15,15] |
| 升力拉偏/% | [-10,10] |
| 再入高度拉偏/km | [-1,1] |
| 再入经度拉偏/km | 对应[-3,3] |
| 再入纬度拉偏/km | [-3,3] |
| 再入速度拉偏/(m·s-1) | [-100,100] |
| 再入轨迹倾角拉偏/(°) | [-0.5,0.5] |
| 再入航向角拉偏/(°) | [-1.0,1.0] |
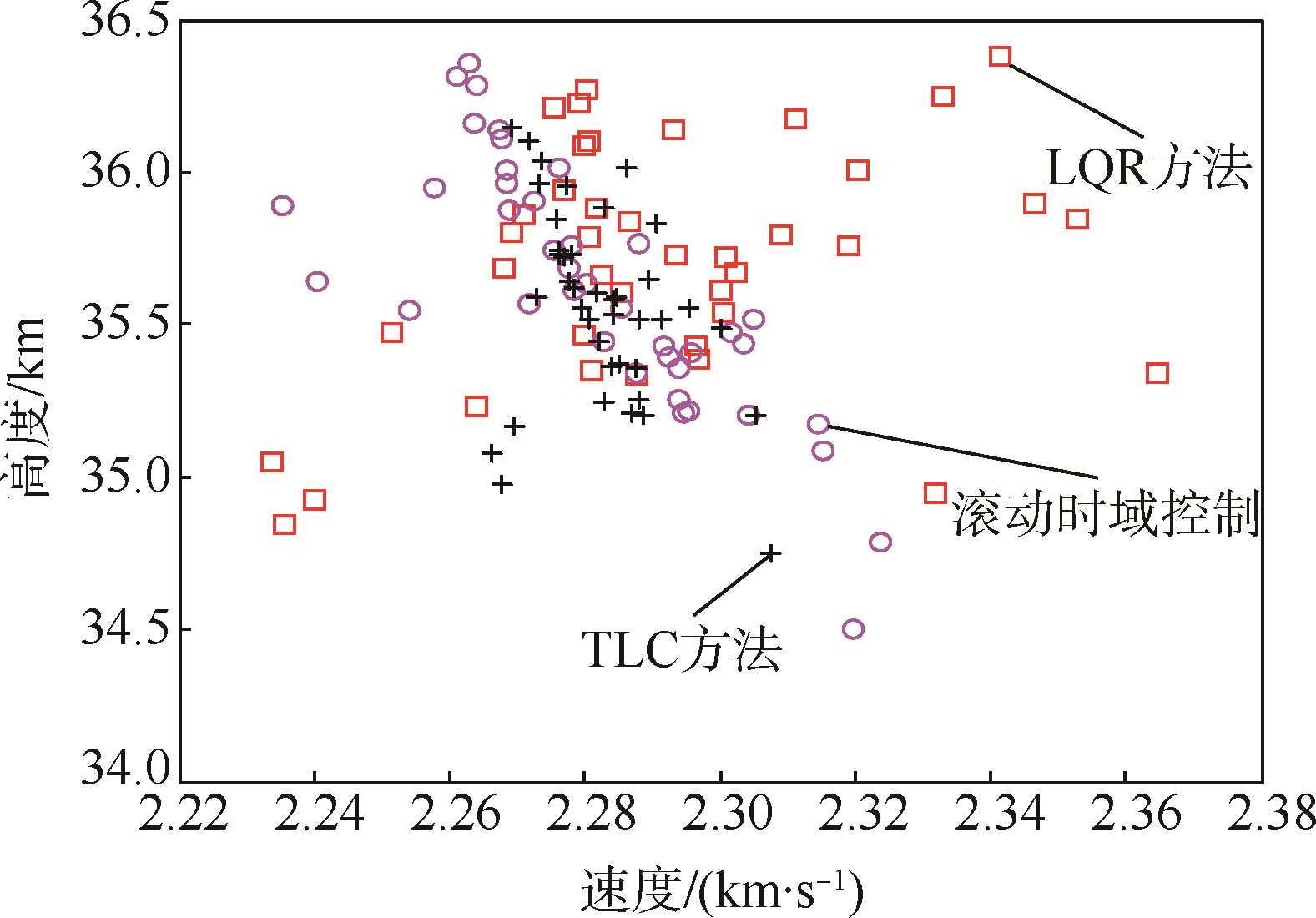 |
| 图 4 速度-高度剖面打靶结果 Fig. 4 Shooting results in velocity-altitude profile |
 |
| 图 5 速度-高度剖面跟踪 Fig. 5 Trajectory tracking in velocity-altitude profile |
 |
| 图 6 航程速度剖面的速度跟踪 Fig. 6 Velocity tracking in range-velocity profile |
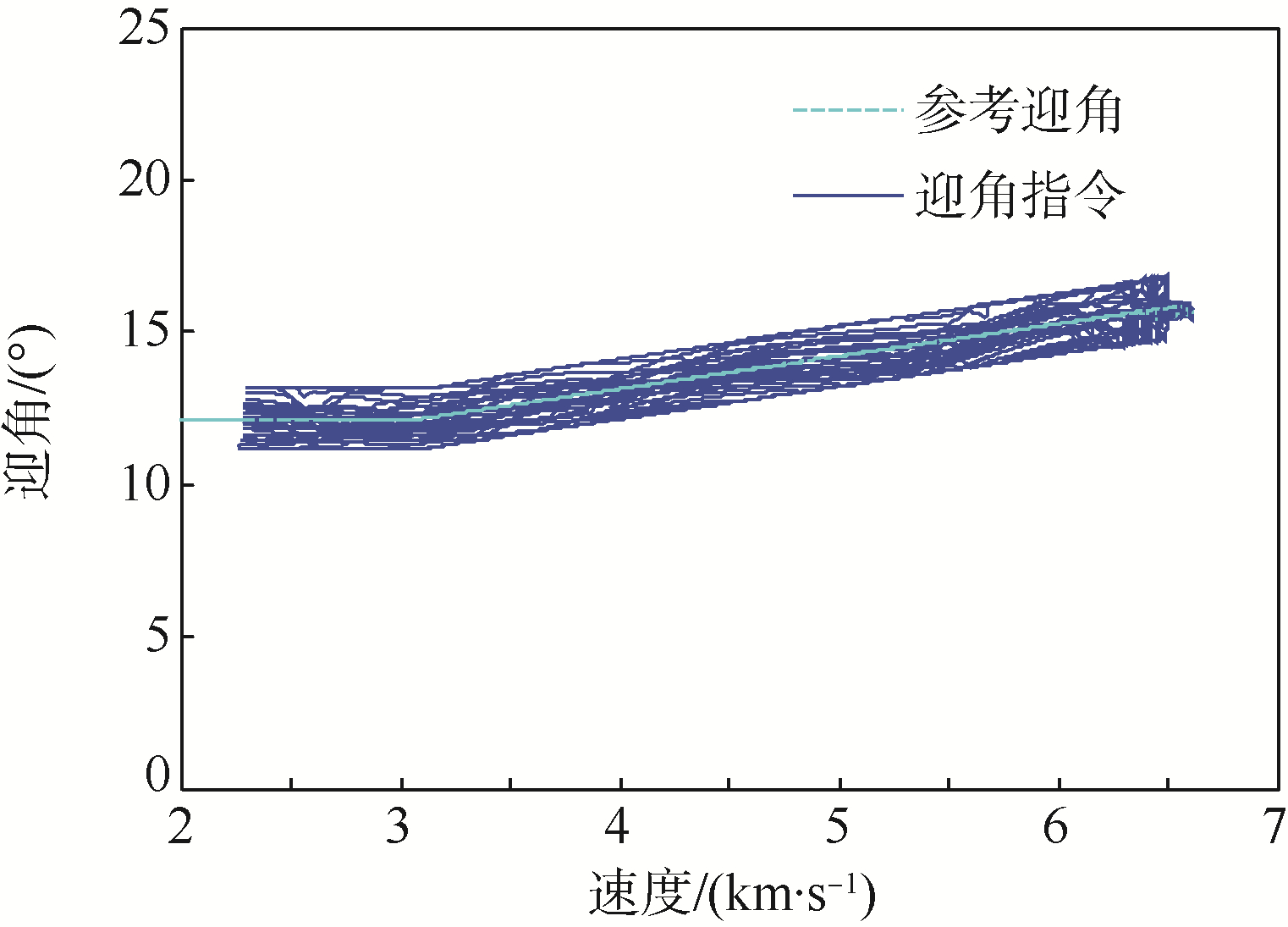 |
| 图 7 迎角控制历程 Fig. 7 Angle of attack command history |
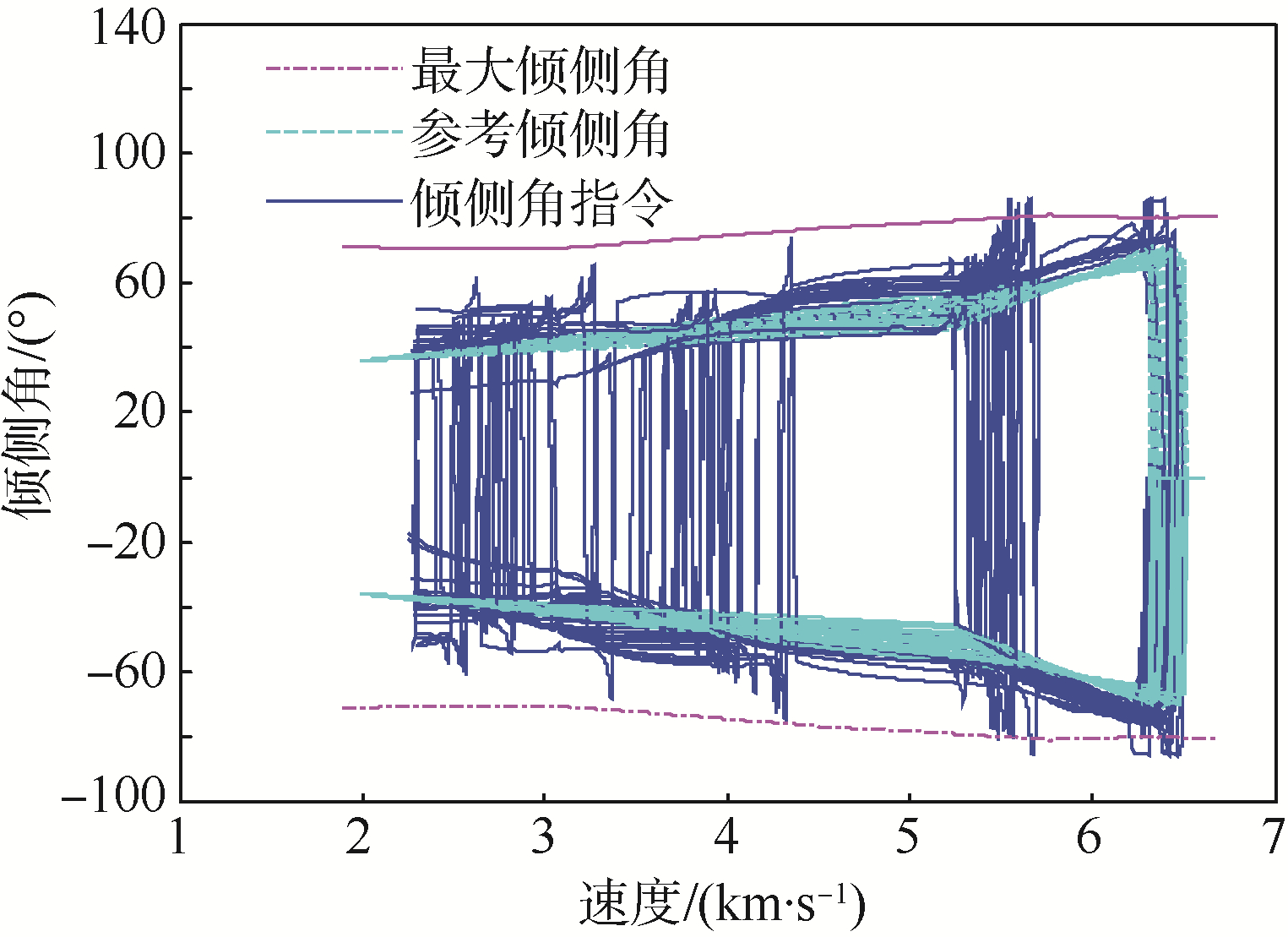 |
| 图 8 倾侧角控制历程 Fig. 8 Bank angle command history |
与LQR方法相比,TLC方法具有更宽的适应范围,其原因在于基于LQR的增益调度方法需要求解Riccati方程,通常难以实时求得最优反馈增益,一般只能根据设计好的参考轨迹离线计算获得后存储于制导计算机.为了适应不同的参考轨迹,只能在地面离线生成多组增益,应用时需要根据实际采用的参考轨迹来选用对应的制导反馈增益.由于设计中通常无法考虑所有的非理想情形,因此采用这类制导律设计具有潜在的风险.而TLC方法不依赖于参考轨迹,反馈增益可以符号化表示为参考轨迹的函数,并只需计算简单的代数式,所需的有限计算量远小于求解Riccati方程和滚动时域控制方法.此外,TLC方法的跟踪精度和增益大小与无量纲自然频率直接相关;对于参考轨迹的不同阶段或差别较大的参考轨迹,通过在线改变不同环路自然频率的数值(同时保证环路间带宽的分离)即可实现期望的控制效果;另外,TLC方法需要调整的参数数量很少且调整的方向性非常明确.这些区别使得TLC方法不仅可以适应更宽范围的再入飞行制导任务,而且与轨迹在线生成算法一起将可极大提高再入制导的自主性,适应于应急再入任务规划、在线任务改变或落点调整等情形.
5 结 论
本文结合在线轨迹生成算法,将TLC方法应用于制导环的轨迹跟踪控制中,与现有经典的LQR方法和近似滚动时域控制的仿真对比和分析表明:
1) TLC方法在初始状态拉偏和扰动情况下也能实现很高的跟踪精度,体现了方法的有效性和鲁棒性.
2) 与LQR方法的仿真结果相比,TLC需要调整的参数更少,参数的选取更直观,对不同参考轨迹有很好的适应性,是一种完全在线的非线性控制方法.与近似滚动时域控制相比,TLC在控制精度略优于前者的情况下计算量显著减小.
3) 在再入轨迹跟踪制导律中使用TLC控制,可以做到制导环和姿态环控制结构的统一和设计时的一体化;高度、速度、姿态角和姿态角速度的四环路TLC控制策略将更便于制导和控制参数的匹配和实时调整.
因此,本文提出的TLC跟踪制导策略对于减少制导指令的解算时间,提高制导的自主性、适应性和精度有一定工程意义.
| [1] | Lu P.Entry guidance:A unified method[J].Journal of Guidance, Control, and Dynamics, 2014, 37(3):713-728. |
| Click to display the text | |
| [2] | Harpold J C, Graves C A Jr.Shuttle entry guidance[J].Journal of Astronautical Sciences, 1979, 27(3):239-268. |
| Click to display the text | |
| [3] | Shen Z J, Lu P.Onboard generation of three-dimensional constrained entry trajectories[J].Journal of Guidance, Control, and Dynamics, 2003, 26(1):111-121. |
| Click to display the text | |
| [4] | Roenneke A J.Adaptive on-board guidance for entry vehicles[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA Inc., 2001:1-10. |
| [5] | Saraf A, Leavitt J A, Chen D T, et al.Design and evaluation of an acceleration guidance algorithm for entry[J].Journal of Spacecraft and Rockets, 2004, 41(6):986-996. |
| Click to display the text | |
| [6] | Bharadwaj S, Rao A V, Mease K D.Entry trajectory tracking law via feedback linearization[J].Journal of Guidance, Control, and Dynamics, 1998, 21(5):726-732. |
| Click to display the text | |
| [7] | Dukeman G A.Profile-following entry guidance using linear quadratic regulator theory[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA Inc., 2002:1-10. |
| Click to display the text | |
| [8] | Lu P.Regulation about time-varying trajectories:Precision entry guidance illustrated[J].Journal of Guidance, Control, and Dynamics, 1999, 22(6):784-790. |
| Click to display the text | |
| [9] | Zhu J, Banker B D, Hall C E.X-33 ascent flight controller design by trajectory linearization-a singular perturbation approach[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA Inc., 2000:1-19. |
| Click to display the text | |
| [10] | Vinh N X, Busemann A, Culp R D.Hypersonic and planetary entry flight mechanics[M].MI, Ann Arbor:University of Michigan Press, 1980:26-27. |
| Click to display the text | |
| [11] | Phillips T H.A common aero vehicle(CAV)model, description, and employment guide[R].[S.l.]:Schafer Corporation for AFRL and AFSPC, 2003. |
| [12] | Zhu J.Nonlinear tracking and decoupling by trajectory linearization[Z].Lecture Note, Presented at NASA Marshall Space Flight Center. |
| [13] | Naidu D S, Calise A J.Singular perturbations and time scales in guidance and control of aerospace systems:A survey[J].Journal of Guidance, Control, and Dynamics, 2001, 24(6):1057-1078. |
| Click to display the text | |
| [14] | Mease K D.Multiple time-scales in nonlinear flight mechanics:Diagnosis and modeling[J].Applied Mathematics and Computation, 2005, 164(2):627-648. |
| Click to display the text | |
| [15] | Lu P, Shen Z J.Unifying treatment to control of nonlinear systems with two timescales[J].Journal of Guidance, Control, and Dynamics, 2002, 25(5):975-979. |
| Click to display the text |



