2. 中北大学信息与通信工程学院, 太原 030051
2. School of Information and Communication Engineering, North University of China, Taiyuan 030051, China
多目标跟踪是指利用传感器的量测对目标的状态(包括位置、速度等)进行估计[1, 2].目前多目标跟踪已广泛应用于遥测遥感[3]、飞行器跟踪[4]、可视化目标跟踪[5]以及分布式融合[6]等领域.以最近邻域卡尔曼滤波(Nearest Neighbor Kalman Filter,NNKF)、多假设前提(Multiple Hypothesis Tracking,MHT)和联合概率数据关联(Joint Probabilistic Data Association,JPDA)为代表的传统多目标跟踪方法通过目标和量测之间明确的关联关系进行跟踪.但是,多目标跟踪场景下目标的状态和数目通常随时间的变化而变化.此外受漏检、虚警和杂波等影响,传感器量测同样也随时间变化.由于目标状态、数目、量测的不确定性,在实际中,状态和量测集合的明确关联关系难以建立.
近年来,随机有限集(Random Finite Sets,RFS)理论在多目标跟踪领域得到了广泛的应用.Mahler[7]基于随机有限集理论,提出了概率假设密度(PHD)滤波算法.该算法将目标的状态和量测分别用随机有限集进行表示,通过强度函数的传播,完成对目标状态和数目的估计.PHD算无需目标的状态和量测的关联,其计算复杂度低于传统的多目标跟踪算法[8].但是PHD算法在估计过程中涉及多维积分,在实际中,这类多维积分通常没有解析解.Vo等[9]将序贯蒙特卡罗(SMC)算法的思想应用于PHD滤波,提出了序贯蒙特卡罗PHD(SMC-PHD)滤波算法.该算法将PHD方程中多维积分转换成多个具有一定权值的样本(也称为粒子)的求和,避免了多维积分的求解.由于该方法具有实现简单、估计精度高的优点,因此引起了国内外众多学者的关注.
文献[10, 11, 12]使用状态转移密度函数作为重要性采样函数,极大简化了SMC-PHD的计算.但是这类算法忽略了当前量测集对目标状态估计的影响,当目标非线性运动时,会导致少量粒子具有大的权值,造成估计误差增大.Punithakumar等[13]通过使用多个运动模型混合作为目标运动模型,将模型转移概率函数作为重要性采样函数,提高了非线性运动目标的估计精度.但是该算法跟踪性能依赖于多模型的选择.文献[14]将辅助粒子滤波的思想引入SMC-PHD,通过在SMC-PHD算法的重要性采样函数设计中引入辅助变量,使得重要性采样函数抽样产生的粒子权值具有最小的方差.与传统的SMC-PHD算法相比,基于辅助粒子滤波的SMC-PHD算法提高了跟踪的精度,但是在严重的非线性或强状态噪声场景下该算法会出现很大的跟踪误差.Yoon等[15]将无迹信息滤波(UIF)应用于SMC-PHD,提高了非线性目标的跟踪精度.但是UIF中Sigma点的选择对算法跟踪性能影响较大.Li等[16]将Sigma门引入SMC-PHD的更新,提出了高速Sigma-gating SMC-PHD算法.该算法仅使用目标周围的量测进行粒子更新,减少了SMC-PHD的计算量.
综上所述,目前常用的SMC-PHD算法多采用状态转移密度作为重要性采样函数,忽略了当前量测集对重要性采样函数的影响.当目标非线性运动时,这类算法呈现粒子退化、跟踪误差大的缺点.因此本文利用SCKF算法[17]和统计门限技术,提出了一种基于均方根容积粒子的序贯蒙特卡罗PHD(SC-SMC-PHD)算法.本算法主要包括2个部分:
1) 针对传统SMC-PHD在非线性多目标跟踪精度不高、结果易发散问题,本算法将近年来出现的SCKF算法引入SMC-PHD的重要性采样函数设计,提出了基于SCKF的重要性采样函数设计方法.通过利用SCKF在非线性目标跟踪下良好的准确性和稳定性,提高了SMC-PHD的跟踪精度.
2) 针对重要性采样函数设计时重要性采样粒子状态和量测关联关系未知的问题,本文提出了一种基于统计门限技术的量测合并方法.通过计算预测量测与量测集中量测的统计距离,并设定阈值,提取与预测量测接近的量测.在此基础上,对所提取的量测按照统计距离的大小分配不同的权值,从而为重要性采样函数设计提供逼真的量测.
和传统的SMC-PHD算法相比,本文所提出的SC-SMC-PHD算法解决了传统的SMC-PHD算法在非线性多目标跟踪时存在的误差大、粒子退化等问题,具有精度高、结果稳定的优点.
1 SMC-PHD 1.1 PHD令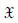
表示状态空间.假设k时刻,目标的状态表示为xk,1,xk,2,…,xk,N,N为目标的数目.显然xk,j∈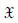.根据随机有限集理论,目标的状态可以用式(1)所示的随机有限集来表示：
式中：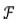
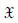()为状态空间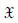中所有闭合的子集.xk,j(j=1,2,…,N)与顺序无关,因此Xk为随机有限集.类似的,假设k时刻单个目标的量测用zk,i(i=1,2,…,M)表示,多目标的量测可以用式(2)来表示：
式中：(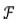
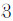)为量测空间Z中所有闭合的子集.
PHD滤波器利用一阶量(也称强度)的传递进行多目标状态和数目的估计.PHD滤波算法进行迭代时,主要包括预测和更新2个步骤.为描述这2个步骤,假定Dk－1|k－1(xk－1|Z1:k－1)为k－1时刻的后验强度,Z1:k－1为k－1时刻之前的所有量测.
1) 预测.假设ps(Xk)为状态Xk的存活概率,则预测强度函数Dk－1|k－1(Xk|Z1:k－1)表示为
式中：fk|k－1(·)为单目标的状态转移密度;γk(·)为新生目标强度.
2) 更新.实际测量过程中,由于漏检、虚警以及杂波等影响,真实量测与理想量测存在差异.考虑这些不利情况,假设k时刻检测概率为pd(Xk),杂波密度为κk(·),后验强度函数为Dk|k(Xk|Z1:k),如式(4)所示:
式中：g(·)为似然函数;Cz可通过式(5)计算得到：
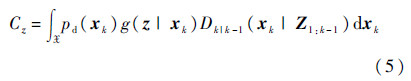
由式(3)和式(4)可以看出,PHD滤波器无需考虑状态集与量测集的关联,仅涉及单个目标在状态空间的积分.由于单个目标状态通常为多维向量,式(3)和式(4)为多维积分,这类积分在实际中很难得到闭合解.针对这一问题,SMC-PHD算法作为一种有效的PHD实现算法便应运而生.
1.2 SMC-PHD简介SMC-PHD滤波算法借鉴粒子滤波的思想,利用重要性采样函数生成大量的粒子,将PHD滤波中的强度函数更新预测转换成粒子集合的预测更新,避免了PHD算法中的多维积分求解.为描述SMC-PHD算法基本原理,定义k－1时刻的粒子集为{xk－1(i),wk－1|k－1(i)}i=1Lk－1,其中,xk－1(i)为由状态xk－1采样生成的第i个粒子状态,wk－1|k－1(i)为其对应的权值.设π(·)和q(·)分别为新生粒子与存活粒子对应的重要性采样函数.在此基础上,SMC-PHD算法的执行流程为[8]
1) 预测.令Jk表示新生粒子的数目,预测强度Dk－1|k－1(Xk|Z1:k－1)表示为
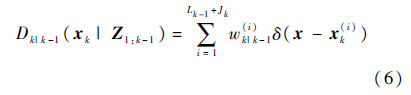
式中:
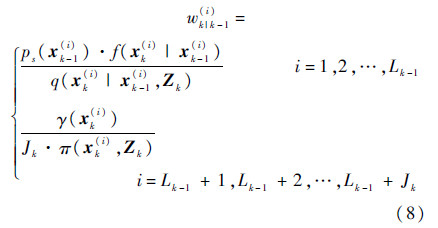
式中:wk|k－1(i)为第i个粒子的预测权值;Jk=ν∫γ(x)dx,ν 为单个新生目标对应的粒子个数.
由式(6)~式(8)可以看出,预测强度Dk－1|k－1(Xk|Z1:k－1)的计算可以通过粒子的权值与状态的预测来实现.
2) 更新.本步骤利用当前量测集Zk对预测强度Dk－1|k－1(Xk|Z1:k－1)函数进行更新,更新得到的后验强度函数为
式中:
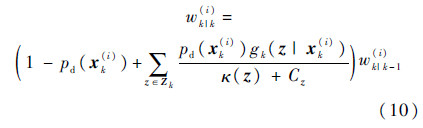
其中：
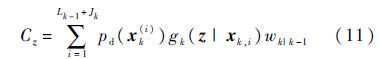
通过上述推导,得到了更新后的粒子集{xk(i),wk|k(i)}i=1N.为提取目标的状态,传统的SMC-PHD滤波通常借助EM(Expectation-Maximum)、K-means等算法[9],对粒子集{xk(i),wk|k(i)}i=1N进行聚类,形成对目标状态和数目的估计.此外,为避免多次迭代造成粒子退化,通常在更新之后引入重采样策略,减少粒子退化对估计造成的影响.
2 均方根容积SMC-PHD算法 2.1 问题描述假设目标的非线性状态和量测方程为
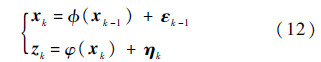
式中：Ф(·)和φ(·)为非线性函数；εk－1和ηk为k－1和k时刻的状态噪声与量测噪声.本文假设εk－1和ηk均为零均值高斯分布,协方差阵分别用Qk－1和Rk表示.
由式(12)易知,Xk和Zk均为高斯分布.为将当前量测引入重要性函数的设计,本文选择后验概率作为式(7)中的重要性采样函数,即
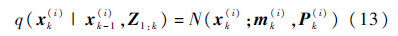
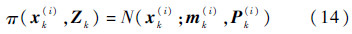
式中：mk(i)和Pk(i)分别为第i个粒子在k时刻的状态均值和协方差矩阵；N(·)表示高斯分布；i的取值范围与式(7)相同.根据式(13)和式(14),重要性采样函数q(xk(i)|xk－1(i),Z1:k)和π(xk(i),Zk)的计算问题可以简化为参数mk(i)和Pk(i)的计算.为解决这一问题,本文利用SCKF算法,通过容积点的更新对mk(i)和Pk(i)进行估计.为描述方便,本文使用mk和Pk代表mk(i)和Pk(i).
2.2 基于SCKF的重要性采样函数估计由前面的讨论,式(13)和式(14)中重要性采样函数可以通过mk和Pk的估计来完成.为实现这一目标,本节提出了一种基于SCKF算法的重要性采样函数估计方法.本方法通过容积点的预测和更新,对当前时刻粒子的均值和协方差进行估计.估计过程包括预测和更新2个步骤.
1) 预测.设k－1时刻的状态和协方差分别为mk－1和Pk－1,Sk－1为Pk－1的均方根(可以通过cholesky分解计算).状态预测时,首先利用三阶容积准则[17]计算容积点,通过容积点传播计算预测状态mk|k－1和预测均方根Sk|k－1.预测过程如下:
① 容积点计算
根据三阶容积准则,容积点集{αj,ρj}可以用式(15)计算:
式中:n为待估计目标状态的维数,αj和ρj分别为第j个容积点的状态及权值;向量[1]j为集合[1]的第j个向量,其中集合[1]为
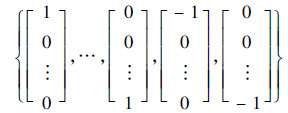
② 计算第j个容积点
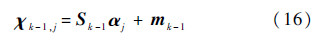
③ 容积点传播
④ 状态预测
⑤ 预测误差协方差矩阵均方根估计
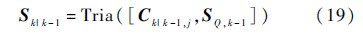
式中:Tria(·)为矩阵的三角分解(本文采用QR分解);SQ,k－1为状态噪声协方差阵Qk－1的均方根,矩阵τk|k－1,j*可通过式(20)计算:
通过上面的计算,便可以得到预测状态mk|k－1及其对应的误差协方差矩阵均方根Sk|k－1.
2) 更新.设zk|k－1为预测的量测,zk,i为当前量测集Zk的第i个量测,SR,k为量测噪声的协方差矩阵均方根,K为卡尔曼滤波增益.与状态预测类似,量测更新时,利用前面得到的mk|k－1和Sk|k－1,通过容积点在量测空间的传播,计算后验状态mk及其对应的误差协方差矩阵Sk.
① 容积点计算
第j个预测容积点可以表示为
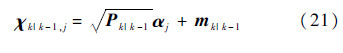
② 容积点传播
将第j个预测容积点代入式(12)的量测方程,可得
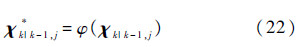
③ 量测预测
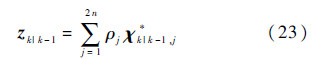
④ 新息均方根协方差矩阵均方根估计
式中:
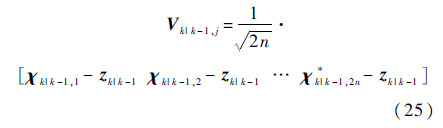
⑤ 互协方差矩阵估计
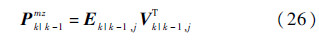
式中：
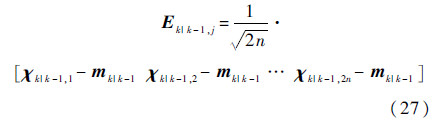
⑥ 卡尔曼滤波增益估计
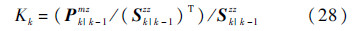
⑦ 状态及协方差矩阵均方根估计
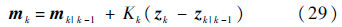
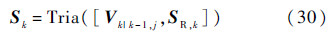
通过预测与更新,最终得到mk和Pk(Pk=SkSkT).
2.3 基于统计门限技术的量测合并由式(29)计算第i个粒子的后验均值mk时,需使用与其关联的量测Zk进行更新.但是在多目标跟踪场景下,当前的量测集往往由多个目标的量测和杂波组成.在标准的SMC-PHD算法中,第i个粒子状态和量测Zk的关联关系通常是未知的.此外,由于杂波在量测空间随机分布,杂波可能出现在目标量测附近,导致估计精度降低.
针对上述问题,本文提出了一种基于统计门限技术的量测合并算法.该算法首先计算重要性采样粒子的预测量测与当前量测集中量测的统计距离,在此基础上,通过设定的阈值,提取与重要性采样粒子相关联的量测集.而后根据统计距离的大小对门限内的量测分配不同的权值,最后对不同权值的量测进行合并,得到重要性采样粒子对应的量测,并用于重要性采样函数的均值更新.
在标准的PHD模型中,每个目标至多只能产生一个量测,反之亦然.所以在SMC-PHD算法中,属于同一目标的粒子至多只能由一个量测与之关联.因此,本文借鉴最近邻法的思想,将统计意义上与粒子量测预测zk|k－1接近的量测作为可能与粒子关联的量测.首先,定义zk|k－1与zk,j(zk,j∈Zk)的统计距离为
根据式(31),通过选取特定的阈值,与第i个粒子关联的量测可以用式(32)的统计门限提取：
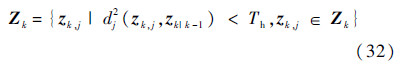
式中:Th为事先设定的阈值;Pkzz为新息协方差阵;Pkzz=Skzz(Skzz)T.
由式(32)得到第 i 个粒子相关联的量测集，为降低门限内杂波对状态更新的影响,本文提出依据门限内量测统计距离的大小,为每个量测分配相应的权值并进行合并,从而抑制关联量测附近杂波对目标状态估计的影响.
令zi∈Zk,其对应的权值可以表示为
式中: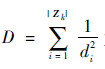 
为归一化因子,显然
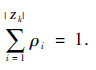由式(33)可知,zk|k－1所对应的量测Zk可以表示为
通过上述的推导,便得到了合并后的量测Zk.将Zk代入式(29),便可以计算粒子的状态均值mk.最后将mk和Pk代入式(13)~式(14),执行式(7)~式(10)的SMC-PHD算法，整体流程如图 1所示.
 |
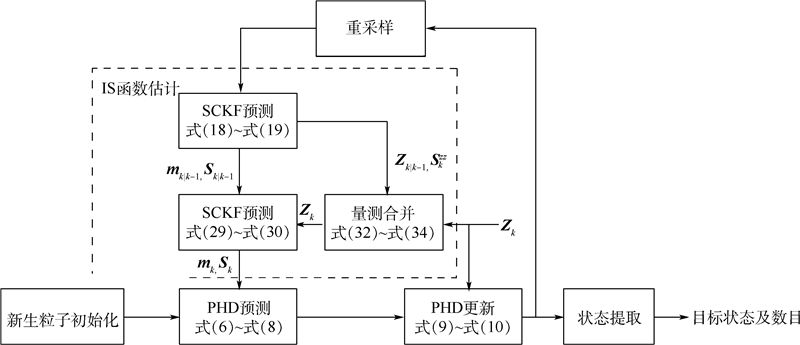| 图 1 SC-SMC-PHD算法执行流程 Fig. 1 Execution process of SC-SMC-PHD algorithm |
图 1中,重采样采用多项式重采样,新生粒子强度初始化和状态提取使用文献[12]的提取算法.
另外，Th的设定可通过查χ2分布表得到.过小的Th将导致大量的量测无法用于更新,增加估计误差;过大的Th则会造成运算量过大.
3 仿真实验本节将对本文所提出的SC-SMC-PHD算法与文献[12]中的IBSMC-PHD算法进行比较.为验证算法的有效性,本文选择最优次模式分配(OSPA)距离[18]和均方根误差(RMSE)作为度量标准.
3.1 实验场景本文采用文献[8]所使用的运动场景.设k时刻目标的状态向量为x=[Xk yk xky αk]T,其中(Xk,yk)为目标的位置；(xk,yk)为速度分量；αk为k时刻的转弯速率.目标的运动方程为
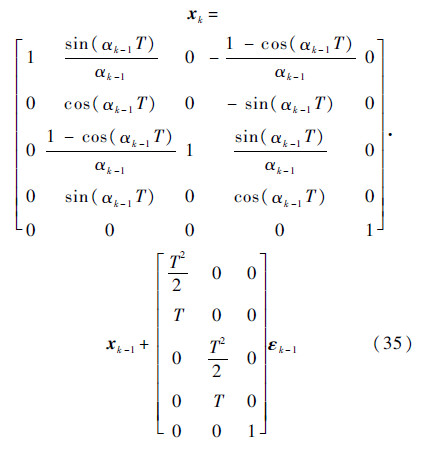
量测方程为
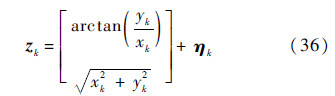
仿真所采用的电脑CPU为Intel双核2.93 GHz,内存2 GB,MATLAB版本为2013a.场景参数设定如下:目标的状态如表 1所示,目标运动轨迹如图 2所示(杂波数为10).目标存活概率ps(Xk)=0.99,检测概率pd(Xk)=0.95,统计距离门限Th=16,每个存活目标和新生目标对应的粒子数分别为5和100.
| 目标序号 | 起始状态 | 出现时间/s | 消失时间/s |
| 1 | [325 5 375 5 0] | 2 | 30 |
| 2 | [500 5 300 5 0] | 15 | 40 |
| 3 | [400 5 475 -5 0] | 25 | 55 |
| 4 | [300 5 450 -5 0] | 44 | 70 |
| 5 | [275 -5 375 5 0] | 44 | 70 |
 |
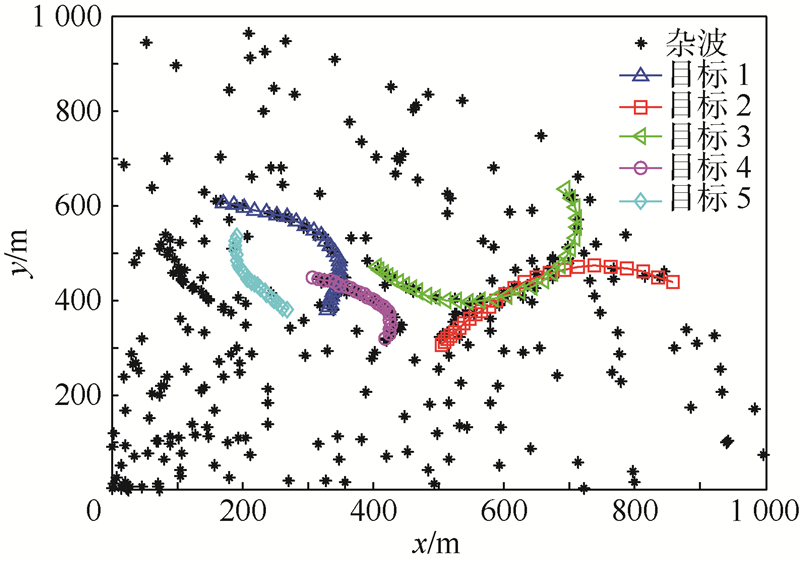| 图 2 目标的真实航迹 Fig. 2 Ground-truth tracks of targets |
仿真1 不同门限下的算法性能.
为验证阈值对算法性能的影响,根据χ2分布表,本文将统计门限距离分别取4、16、25、49以及81.为分析跟踪精度,本文使用OSPA距离和估计数目的RMSE等作为衡量指标.
本文提出的SC-SMC-PHD算法经500次蒙特卡罗结果如表 2所示.
| 门限 | 平均OSPA/m | 平均RMSE |
| 4 | 26.56 | 0.28 |
| 16 | 25.34 | 0.26 |
| 25 | 25.91 | 0.27 |
| 49 | 26.51 | 0.28 |
| 81 | 27.52 | 0.29 |
由表 2可知,随着门限的增大,平均OSPA和RMSE的增幅不大.这说明SC-SMC-PHD算法采用统计门限合并的方法,具有良好的稳定性.
仿真2 不同量测误差的算法性能.
改变量测噪声中距离均方根偏差,使用SC-SMC-PHD算法跟踪图 2的目标,500次蒙特卡罗仿真结果如图 3和图 4所示.
 |
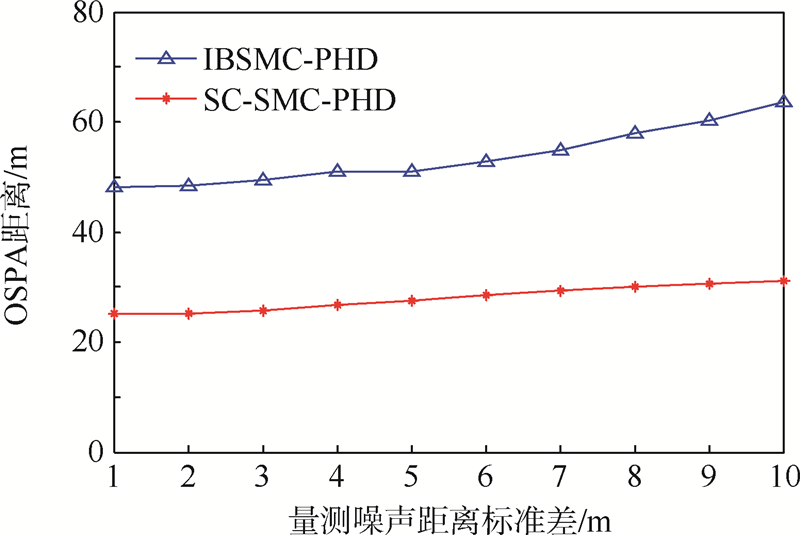| 图 3 不同量测噪声距离标准差下的OSPA距离 Fig. 3 OSPA distances under different range standard deviations of observation noise |
 |
| 图 4 不同量测噪声距离标准差下的RMSE Fig. 4 RMSEs under different range standard deviations of observation noise |
由图 3和图 4可知,当量测噪声标准差从1 m变化到10 m时,SC-SMC-PHD算法的变化趋势小于IBSMC-PHD算法.这说明本算法在量测噪声增大时仍能保持良好的跟踪精度.
仿真3 固定杂波下多目标跟踪性能对比.
对图 2的目标分别使用SC-SMC-PHD算法与IBSMC-PHD算法进行估计,每种算法各进行500次蒙特卡罗仿真,本算法执行所需时间为0.14 s,而IBSMC-PHD为0.13 s.由于IBSMC-PHD使用状态转移函数f(xk(i)|xk－1(i))作为重要性采样函数q(xk(i)|xk－1(i),Zk),避免了式(8)的重要性函数估计,因此其时间复杂度低于本算法.
图 5和图 6分别为IBSMC-PHD和本文提出的SC-SMC-PHD算法500次蒙特卡罗仿真的估计航迹.从图 5和图 6可以看出，IBSMC-PHD算法在对目标1,目标4和目标5估计时,多数的估计值和真实目标位置重合.但是对具有强非线性运动的目标2和目标3估计时,IBSMC-PHD算法出现了大量的目标丢失.相比而言,本文提出的SC-SMC-PHD算法对上述5个目标均具有良好的估计效果,如图 6所示.
 |
| 图 5 IBSMC-PHD算法估计航迹 Fig. 5 Estimated tracks of IBSMC-PHD algorithm |
 |
| 图 6 SC-SMC-PHD算法估计航迹 Fig. 6 Estimated tracks of SC-SMC-PHD algorithm |
首先分析SC-SMC-PHD和IBSMC-PHD算法对起始航迹的跟踪效果,这里使用文献[19]所定义的虚假航迹起始概率和目标正确起始概率作为衡量标准.SC-SMC-PHD的虚假起始概率为0.13,IBSMC-PHD为0.41,目标的正确起始概率如表 3所示.由表 3可以看出,对各目标的正确起始概率而言,SC-SMC-PHD算法均高于IBSMC-PHD算法.尤其是对同时出现目标4和目标5时而言,IBSMC-PHD算法几乎无法获取二者起始航迹.相比而言SC-SMC-PHD算法仍能保持良好的识别概率.
| 目标序号 | SC-SMC-PHD | IBSMC-PHD |
| 1 | 0.97 | 0.89 |
| 2 | 0.84 | 0.75 |
| 3 | 0.88 | 0.57 |
| 4 | 0.83 | 0.09 |
| 5 | 0.87 | 0.12 |
为进一步对比二者的跟踪性能,图 7为二者的OSPA距离,其中SC-SMC-PHD算法的平均OSPA距离为27.87 m,而IBSMC-PHD算法的平均OSPA距离为47.82 m.由图 7可以看出,从第26 s到第55 s内,IBSMC-PHD算法的OSPA距离具有较大的波动,其余时间内二者OSPA距离接近,这是因为从第26 s到第55 s内,具有强非线性运动的目标2和目标3的存在造成了IBSMC-PHD算法的估计误差增大.由于本文所提出的SC-SMC-PHD算法将当前的量测引入重要性采样函数的设计,并使用SCKF与Gating技术进行重要性函数的估计,因此在整个跟踪时间内,本算法具有相对稳定的跟踪效果.此外,从图中还可以看出,在2、15、25和45 s处,SC-SMC-PHD算法的OSPA曲线出现4个峰值,这代表在这些时刻有新的目标出现,因此SC-SMC-PHD算法可以准确地检测目标的出现.
 |
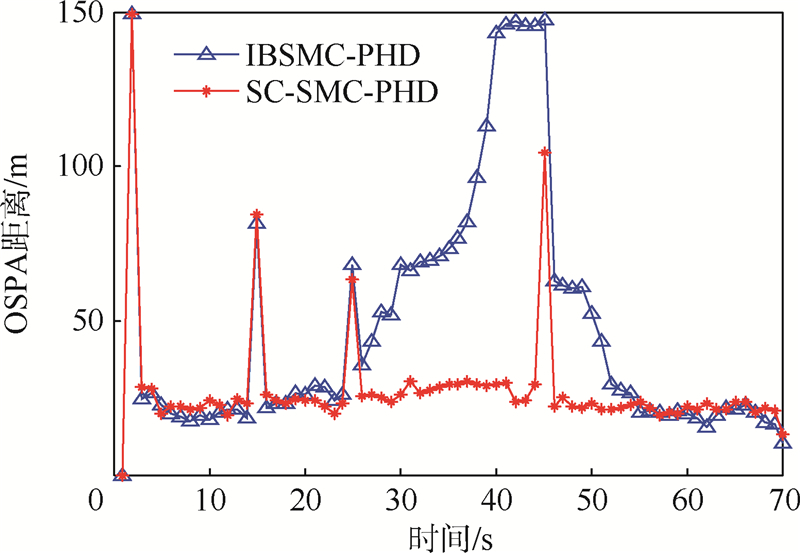| 图 7 OSPA距离 Fig. 7 OSPA distances |
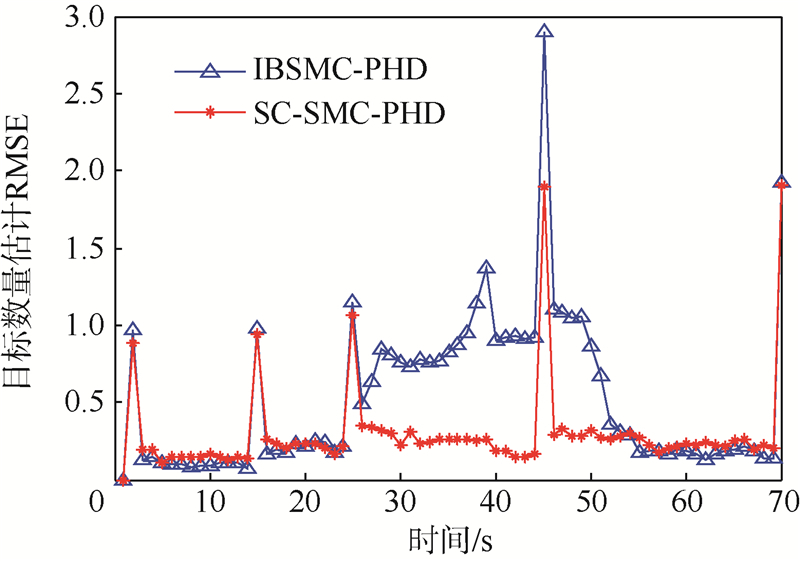
从图 8的目标数目估计曲线可以看出,和IBSMC-PHD算法相比,SC-SMC-PHD算法的目标数目估计曲线更加接近真实目标数目曲线.图 9为图 8目标数目估计的RMSE曲线,图中SC-SMC-PHD算法的平均RMSE为0.26,IBSMC-PHD算法为0.53.与图 7类似,第26 s到第55 s内,IBSMC-PHD算法的RMSE曲线出现较大的波动,而SC-SMC-PHD算法的估计曲线在1~70 s比较稳定.从图 7到图 9,可以看出,通过本文所提出的重要性采样函数设计方法,SC-SMC-PHD算法明显优于IBSMC-PHD算法,但其时间复杂度略高于IBSMC-PHD算法.
 |
| 图 8 目标数目估计 Fig. 8 Estimated target numbers |
 |
| 图 9 目标数目估计RMSE Fig. 9 RMSEs of estimated target numbers |
仿真4 不同杂波下多目标跟踪性能对比.
为验证算法在不同杂波下跟踪的稳定性,改变图 2中的杂波数目,对SC-SMC-PHD与IBSMC-PHD分别进行500次蒙特卡罗仿真.表 4为各算法的平均OPSA距离和RMSE.从表 4中可以看出,随着杂波数目的增加,IBSMC-PHD的平均OSPA距离和RMSE急剧增大,而SC-SMC-PHD算法变化比较缓慢.这表明,本文所提出的SC-SMC-PHD算法在不同杂波环境下具有良好的稳定性.这是因为SC-SMC-PHD算法在重要性采样函数设计时引入了当前量测估计重要性采样函数.由于SCKF在非线性估计中良好的跟踪性能,SC-SMC-PHD算法具有较小的OSPA距离.此外,由于本算法使用了基于Gating技术的量测合并算法,减小了杂波对估计精度的影响,因此在不同的杂波环境下具有良好的稳定性.
| 杂波数目 | 平均OSPA | 平均RMSE | ||||
| IBSMC-PHD/m | SC-SMC-PHD/m | 提升/% | IBSMC-PHD | SC-SMC-PHD | 提升/% | |
| 1 | 44.57 | 21.62 | 51.59 | 0.49 | 0.21 | 57.14 |
| 10 | 47.92 | 24.64 | 48.58 | 0.53 | 0.25 | 52.83 |
| 20 | 52.54 | 30.95 | 41.09 | 0.53 | 0.34 | 35.85 |
| 30 | 57.45 | 39.08 | 31.98 | 0.61 | 0.43 | 29.51 |
| 40 | 63.62 | 47.07 | 26.01 | 0.68 | 0.55 | 19.12 |
本文将SCKF和统计门限技术引入SMC-PHD的重要性采样函数设计,提出了一种SC-SMC-PHD算法.仿真实验表明:
1) 在固定/不同杂波数目下,和传统的SMC-PHD算法相比,本算法具有较高的准确性.当杂波数在1~50变化时,本算法的精度提升达到30%以上,但时间复杂度略高于传统SMC-PHD算法.
2) 在不同的门限和量测噪声水平下,本算法能保持良好的稳定性.
3) 本算法使用了传统的多项式重采样算法,仍存在粒子退化的问题,后续的研究将对其进行完善.
| [1] | Bocquel M, Driessen H, Bagchi A.Multitarget tracking with interacting population-based MCMC-PF[C]//IEEE 15th International Conference on Information Fusion(FUSION).Piscataway, NJ:IEEE Press, 2012:74-81. |
| Click to display the text | |
| [2] | Ristic B.Particle filters for random set models[M].New York:Springer, 2013. |
| [3] | Mallick M, Vo B N, Kirubarajan T, et al.Introduction to the issue on multitarget tracking[J].IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3):373-375. |
| Click to display the text | |
| [4] | Vermaak J, Godsill S J, Perez P.Monte carlo filtering for multi target tracking and data association[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(1):309-332. |
| Click to display the text | |
| [5] | Wu J, Hu S, Wang Y.Adaptive multifeature visual tracking in a probability-hypothesis-density filtering framework[J].Signal Processing, 2013, 93(11):2915-2926. |
| Click to display the text | |
| [6] | Uney M, Clark D E, Julier S J.Distributed fusion of PHD filters via exponential mixture densities[J].IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3):521-531. |
| Click to display the text | |
| [7] | Mahler R P S.Multitarget Bayes filtering via first-order multitarget moments[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4):1152-1178. |
| Click to display the text | |
| [8] | 杨峰, 王永齐, 梁彦, 等.基于概率假设密度滤波方法的多目标跟踪技术综述[J].自动化学报, 2013, 39(11):1944-1956. Yang F, Wang Y Q, Liang Y, et al.A survey of PHD filter based multi-target tracking[J].Acta Automatica Sinica, 2013, 39(11):1944-1956(in Chinese). |
| Cited By in Cnki | |
| [9] | Vo B N, Singh S, Doucet A.Sequential Monte Carlo methods for multitarget filtering with random finite sets[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4):1224-1245. |
| Click to display the text | |
| [10] | Mahler R P S.Statistical multisource-multitarget information fusion[M].Norwood:Artech House, Inc., 2007. |
| [11] | Ristic B, Clark D, Vo B N.Improved SMC implementation of the PHD filter[C]//13th Conference on Information Fusion(FUSION).Piscataway, NJ:IEEE Press, 2010:1-8. |
| Click to display the text | |
| [12] | Ristic B, Clark D, Vo B N, et al.Adaptive target birth intensity for PHD and CPHD filters[J].IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2):1656-1668. |
| Click to display the text | |
| [13] | Punithakumar K, Kirubarajan T, Sinha A.Multiple-model probability hypothesis density filter for tracking maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1):87-98. |
| Click to display the text | |
| [14] | Baser E, Efe M.A novel auxiliary particle PHD filter[C]//IEEE 15th International Conference on Information Fusion(FUSION).Piscataway, NJ:IEEE Press, 2012:165-172. |
| Click to display the text | |
| [15] | Yoon J H, Kim D Y, Yoon K J.Efficient importance sampling function design for sequential Monte Carlo PHD filter[J].Signal Processing, 2012, 92(9):2315-2321. |
| Click to display the text | |
| [16] | Li T, Sun S, Sattar T P.High-speed sigma-gating SMC-PHD filter[J].Signal Processing, 2013, 93(9):2586-2593. |
| Click to display the text | |
| [17] | Arasaratnam I, Haykin S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control, 2009, 54(6):1254-1269. |
| Click to display the text | |
| [18] | Schuhmacher D, Vo B T, Vo B N.A consistent metric for performance evaluation of multi-object filters[J].IEEE Transactions on Signal Processing, 2008, 56(8):3447-3457. |
| Click to display the text | |
| [19] | 汤琦, 黄建国, 杨旭东.航迹起始算法及性能仿真[J].系统仿真学报, 2007, 19(1):149-152. Tang Q, Huang J G, Yang X D.Algorithm of track initiation and performance evaluation[J].Journal of System Simulation, 2007, 19(1):149-152(in Chinese). |
| Cited By in Cnki |