2. 电磁散射重点实验室, 北京 100854
2. Science and Technology on Electromagnetic Scattering Laboratory, Beijing 100854, China
隐身技术是当今世界各国普遍关注的重要军事技术之一.其实质是降低目标的雷达散射截面(RCS)[1],加载雷达吸波材料(RAM)是实现RCS减缩的一种主要技术途径.
20世纪30年代就出现了雷达吸波材料,并应用于天线领域.随着雷达技术的发展,20世纪50年代以后,出现了众所周知的Salisbury屏[2]、Dallenbach和Jaumann吸收体[3],它们的吸波原理主要有两种:相位抵消或者直接吸收入射电磁波的能量.后来,为了提高RAM的性能,开发了一些新型材料,诸如铁氧体、频率选择表面(FSS)[4]、纳米材料吸收剂等.但是,常规的RAM一旦制造出来其特性便是固定的,吸收带宽是有限的[5],如果战场环境和所面临的威胁发生改变,它的隐身效能便会大打折扣.
智能隐身概念的提出,为RAM的发展提供了更为广阔的空间.智能隐身系统是一种能够从自身的表层或内部获取关于环境条件及其变化的信息,随后进行判断、处理、反应,以改变自身的结构与功能,使之很好地与外界相协调地具有自适应性的材料系统.智能隐身系统主要由电子侦察设备、控制器、控制电压或调制波形产生器和有源可调微波吸收体组成.智能隐身系统的工作流程是:首先由电子侦察设备捕捉敌方雷达的威胁频率,将它反馈给控制器;然后控制器根据威胁频率作用于控制电压或调制波形产生器,使其产生相应的控制电压或调制波形;最后所产生的控制电压或调制波形作用于可调微波吸收体,使其在威胁频率处获得最佳的吸波性能.
有源可调微波吸收体是智能隐身系统的关键部件,它可以根据武器装备所面临的威胁频率,采用电控方式动态调整吸收体阻抗的实部或虚部,使在威胁频率处获得最佳吸波性能.因此,研究有源可调微波吸收体具有重大意义.
20世纪90年代,英国的Parker等提出在频率选择表面中加入PIN二极管构成有源FSS结构,通过调节二极管的偏置电压或偏置电流,可以改变FSS的谐振特性[6].2004年英国谢菲尔德大学教授Tennant和Chambers设计了领结型FSS有源雷达吸收体[7].该结构选择PIN管作为可控元件,经测试该有源FSS吸波屏对垂直极化的平面波在9~13 GHz内实现了吸波特性的可调;该成果主要实现了反射率深度的电流控制,而谐振点或工作频段的可控迁移效果并不明显.东南大学的徐欧和朱敏设计了双方环FSS单元可调微波吸收体,并开展了进一步的实验研究[8].
本文设计并研制了一种方环可调微波吸收体的实验样板,并进行了反射率测量.在此基础上,从工程应用角度出发,研究了十字型单元可调微波吸收体的优化设计技术,为宽频段、高吸收、双极化雷达吸波材料的研究和开发提供了一种新途径.
1 可调微波吸收体无源结构型吸波材料包括Salisbury屏或Jaumann型及渐变介质型两大类.有源吸波结构是在上述两种类型基础上发展起来的.综合考虑隐身效果、设计和加工难度及响应速度等多种因素,本文采用以Salisbury屏为基础的可调微波吸收体.可调微波吸收体是在Salisbury屏(见图 1)的基础上发展起来的.在Salisbury屏的阻抗层中引入电抗成分可形成电路模拟吸收体[9, 10](见图 2);对阻抗层的电阻或电抗进行电控,就形成了可调微波吸收体.可调微波吸收体由金属背衬、介质间隔层、可变阻抗层组成,如图 3所示(电阻与电导、电抗与电纳、阻抗与导纳互为倒数关系).
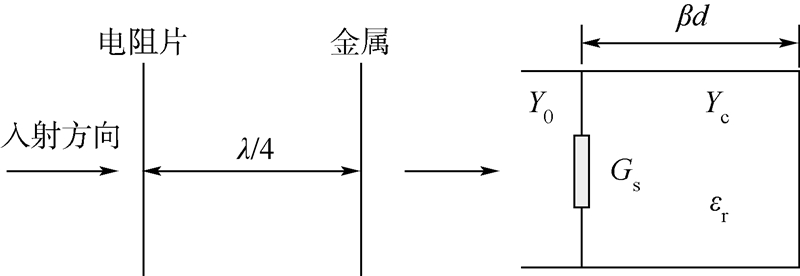 |
| λ—波长;Y0—自由空间导纳;Yc—间隔层本征导纳;d—间隔层材料厚度;β—相移常数;εr—间隔层介电常数;Gs—阻抗层电导. 图 1 Salisbury屏及传输线等效电路Fig. 1 A Salisbury screen and transmission line equivalent circuit |
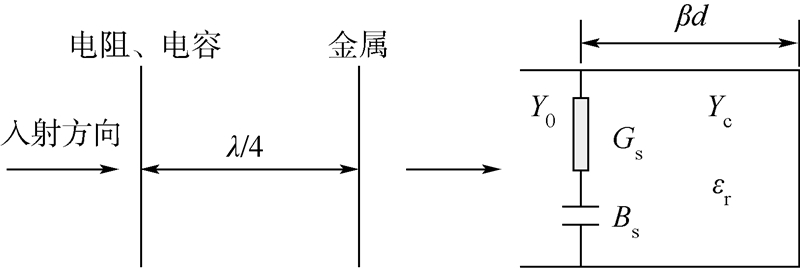 |
| 图 2 电路模拟吸收体及传输线等效电路Fig. 2 A circuit analog absorber and transmission line equivalent circuit |
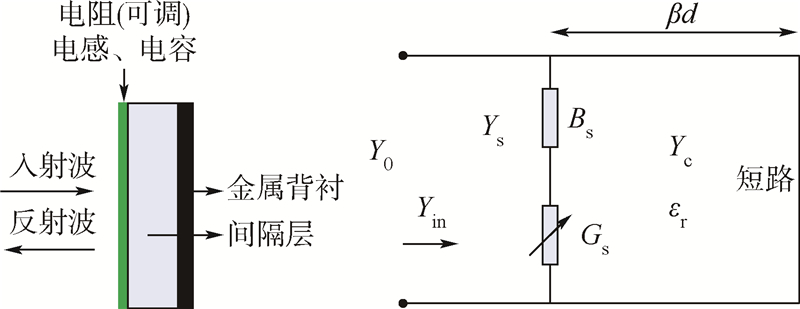 |
| 图 3 可调微波吸收体及其传输线等效电路Fig. 3 A tunable microwave absorber and transmission line equivalent circuit |
根据传输线理论,法向入射时的反射系数为
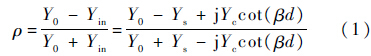
1) Salisbury屏,频带窄,不可调. 当Ys=Y0,d=λ/4,cot(βd)=0,ρ→0,其中反射系数ρ用传输线理论对不同隔离层介质的反射率进行计算,结果见图 4(取电阻R=377 Ω,隔离层厚度为7.5 mm).
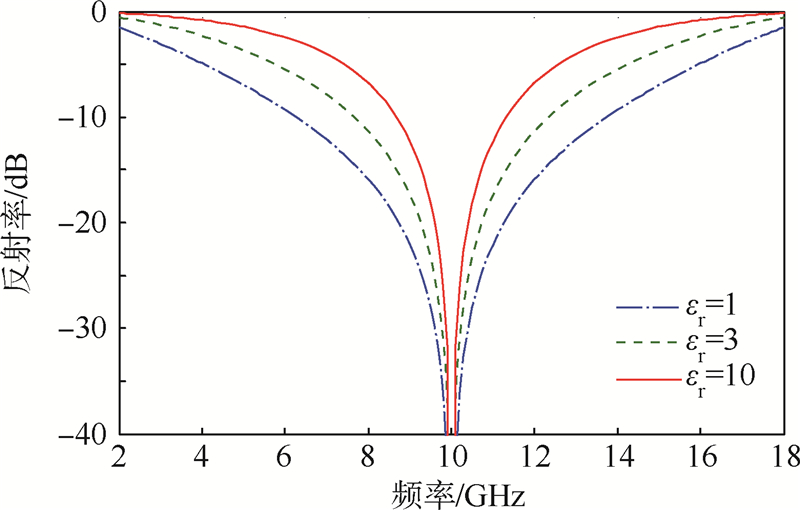 |
| 图 4 加载不同材料后Salisbury屏的反射特性Fig. 4 Reflectivity characteristics of Salisbury screens designed with different materials |
从图 4看出,Salisbury屏频带窄,且随着间隔层介电常数增大,吸波性能变差.
2) 电路模拟吸收体,频带宽,不可调.
用等效电路法[11, 12, 13]和HFSS对单层电路模拟吸收体(间隔层、蒙皮材料介电常数为4,厚度分别为1.87 mm和3.16 mm,阻抗层采用方形贴片:FSS单元周期p=7.5 mm,FSS单元间距g=1.3 mm,电阻R=60 Ω)的反射率进行计算,仿真曲线如图 5所示.
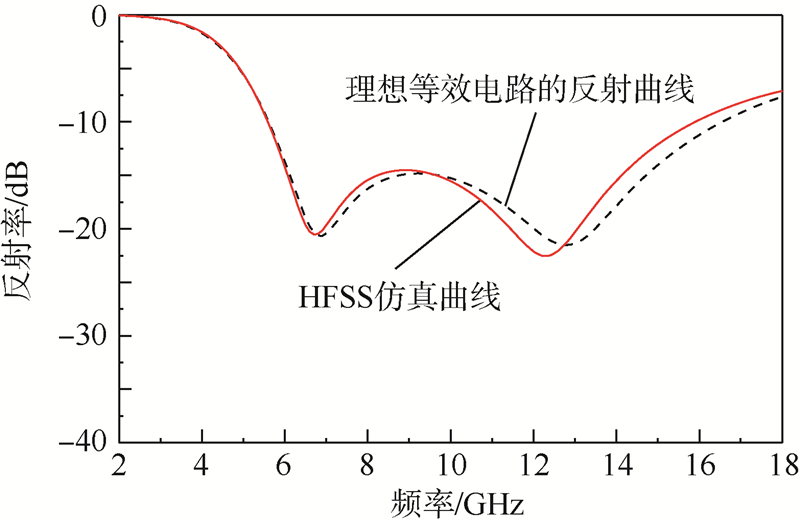 |
| 图 5 单层电路模拟吸收体的反射特性Fig. 5 Reflectivity characteristics of a single-layer circuit analog absorber |
3) 可调微波吸收体,高吸收,频带宽,且可调. 图 3中,当Bs为容性时

有源吸波结构的谐振频率由式(2)中虚部确定.调节R(Gs)或C可以调谐频率,同时改变反射率的“0”深.
图 6所示为固定Bs,改变Gs(R)时的可调微波吸收体(厚度为5.3 mm)反射率仿真结果,当R变化时,最低反射率“0”深和反射率位置相应改变.
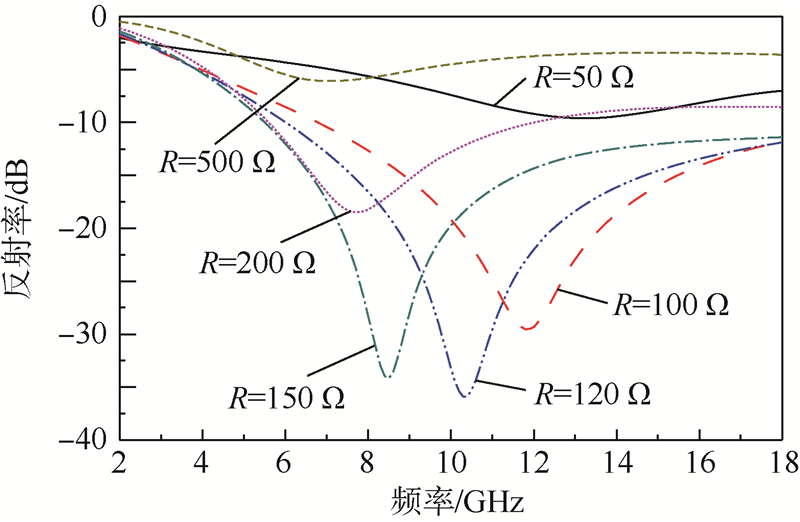 |
| 图 6 R取值不同时可调微波吸收体的反射特性Fig. 6 Reflectivity characteristics of a tunable microwave absorber with different R |
根据表 1,比较Salisbury屏与电路模拟吸收体看出,引入电纳可以扩展频带;但两者的不足是一旦设计加工完成,其吸波性能也固定.可调微波吸收体的阻抗可调,因而具有更大的吸波带宽.
| 吸波结构类型 | 电阻 | 电纳 | 厚度/波长 | -20 dB相对带宽/% | 带宽/厚度 |
| Salisbury屏 | 固定 | 无 | 0.25 | 25.3 | 1.01 |
| 电路模拟吸收体 | 固定 | 固定 | 0.187 | 34.7 | 1.85 |
| 可调微波吸收体 | 可调 | 固定 | 0.185 | 66.7 | 3.61 |
从工程实际角度出发,实现可变阻抗层的阻抗可调有3种途径:
1) 固定X,改变R.例如FSS串联PIN二极管,通过改变PIN偏置电流改变R.
2) 固定R,改变X.例如有耗FSS串联变容管,通过改变变容管偏置电压,改变电容.
3) R、X均可调.
本文采用由FSS结合PIN二极管组成的阻抗表面方案.通过电流控制PIN二级管的电阻,从而改变整个可变阻抗层的阻抗.PIN二极管响应速度快,响应时间在μs级,功耗约为25 μW/cm2.
2 反射率预估可调微波吸收体如图 7所示:蒙皮层为FR4材料,间隔层为工程泡沫(介电常数为1.1).可变阻抗层由FSS加载PIN二极管组成;本文选取方环FSS单元,并采用整体并联馈电方式加载电流.
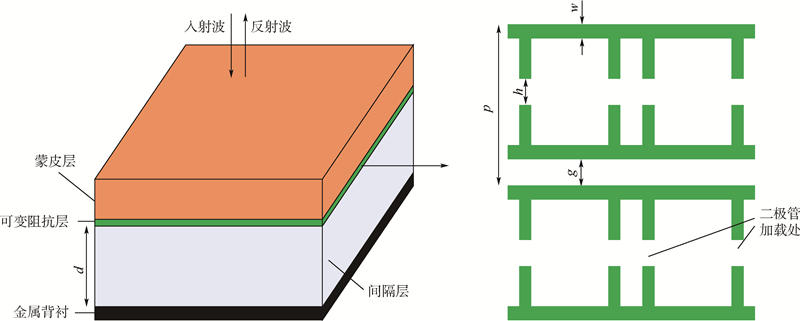 |
| 图 7 方环FSS单元可调微波吸收体示意图Fig. 7 A tunable microwave absorber schematic with square FSS unit |
方环单元周期p=9 mm,间隔g=2 mm,线宽w=0.5 mm.利用有限元分析软件仿真,得到方环可调微波吸收体在垂直入射时的反射率预估曲线(见图 8).二极管电阻在10~1 000 Ω之间变化时,反射率谐振频率相应地变化,低于-15 dB的反射率曲线覆盖了7~13 GHz.
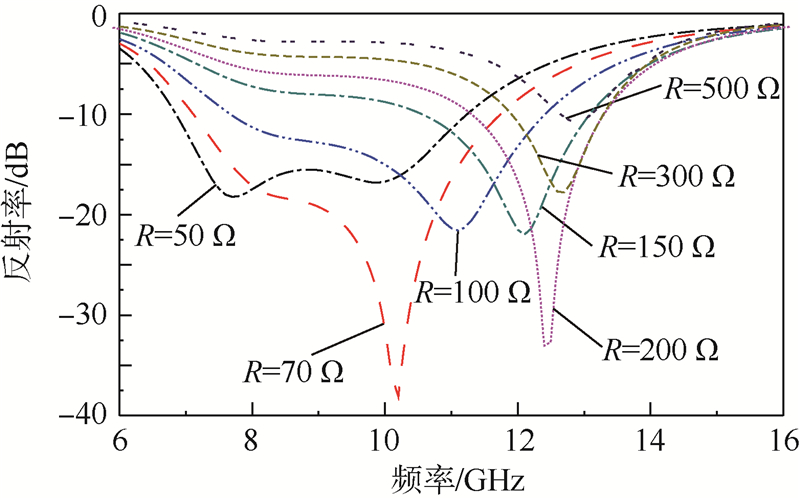 |
| 图 8 可调微波吸收体反射率预估曲线Fig. 8 Predicted reflectivity characteristics curves of tunable microwave absorber |
根据上述结构参数,制作方环可调微波吸收体的实验样板(见图 9).FSS样板长200 mm,宽200 mm.
 |
| 图 9 可调微波吸收体实验样品板Fig. 9 Experimental sample plate of tunable microwave absorber |
实验测试在微波暗室中进行,测量方法采用远场RCS测试法,适合2~18 GHz的反射率测量.图 10为测量装置示意图.其中用到的主要仪器设备有:矢量网络分析仪、发射接收天线、定向耦合器、微波放大器、扫频信号源、样品支架与转台、电流源等.反射率测量过程按照GJB 2038—1994标准执行,得到的测试曲线如图 11所示.当二极管偏置电流I为0 mA时,吸收体几乎没有吸波效果;偏置电流为0.05 mA时,吸收体的最佳吸波频率为12 GHz,最低反射率为-20 dB.随着偏置电流越来越大,吸收体的最佳吸波频率越来越小(见表 2);偏置电流为0.5 mA时,吸收体的最佳吸波频率达到7.5 GHz.
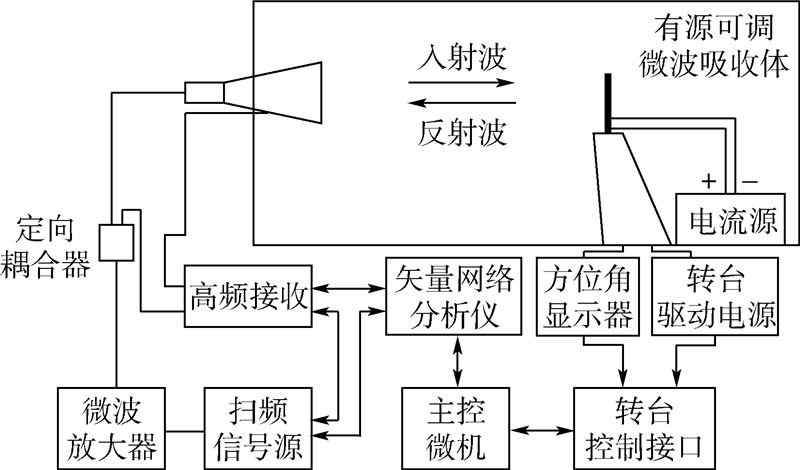 |
| 图 10 远场RCS测试系统组成Fig. 10 Composition of far field RCS measured system |
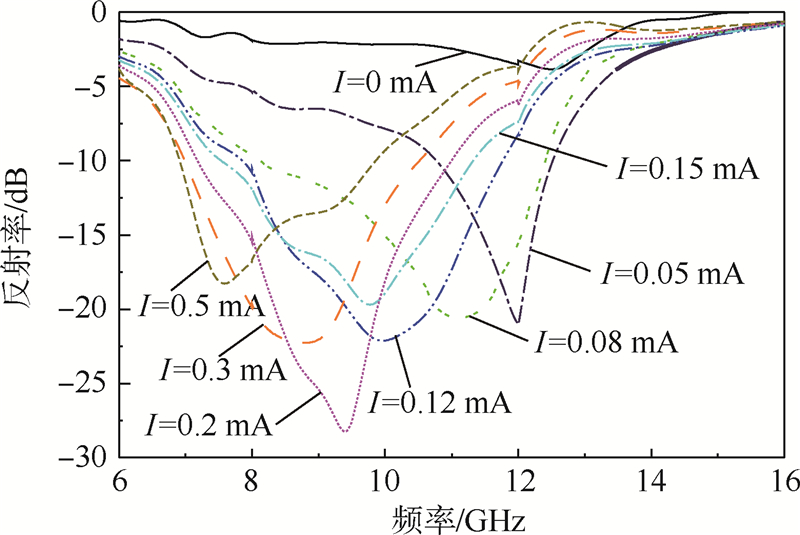 |
| 图 11 可调微波吸收体反射率特性测量曲线Fig. 11 Measured reflectivity characteristics curves of tunable microwave absorber |
| 偏置电流/mA | 最佳吸波频率/GHz |
| 0.05 | 12 |
| 0.08 | 11 |
| 0.12 | 10 |
| 0.15 | 9.7 |
| 0.2 | 9.4 |
| 0.3 | 9 |
| 0.5 | 7.5 |
从图 11可以看出,当二极管偏置电流在0~0.5 mA变化时,该实验板对垂直极化的平面波在7~12.5 GHz内实现了吸波特性的可调.与图 8比较可以看出,实验与仿真结果基本一致.
4 优化设计可调微波吸收体的设计是一个多变量的优化问题.因为反射系数是涉及材料参数、间隔层厚度、FSS的形状尺寸等的函数,这些变量有合理的取值范围.优化的目的就是在这些取值范围内,找出一组最优解,使得设计出的可调微波吸收体具有最优的吸波性能.应用遗传算法[14, 15, 16]使这个很复杂的问题变得切实可行,只要变量的搜索空间不是特别庞大的话,很快就可以找到期望的答案.
针对可调微波吸收体,本文编制了基于遗传算法的优化程序.为了实现超宽带以及双极化的目的,本文设计了一种中心对称的十字型FSS单元结构(见图 12).
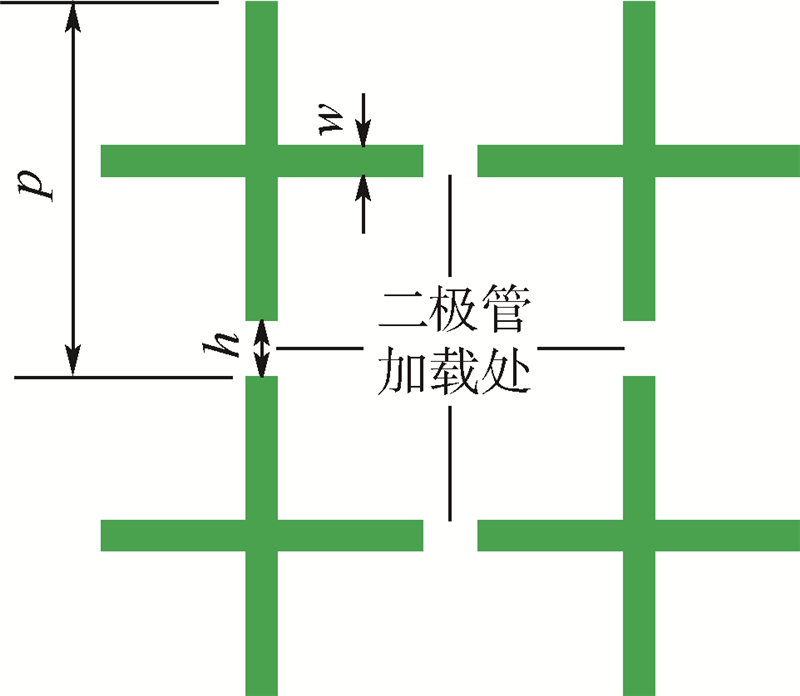 |
| 图 12 十字型有源FSS示意图Fig. 12 Schematic diagram of cross active FSS |
利用反射率优化程序,设定参数后,得到最终优化结果:p=5.3 mm,w=0.5 mm,二极管长度h=1 mm,间隔层厚度为5.6 mm,蒙皮层厚度为1.8 mm.仿真结果如图 13所示,吸收体的反射频率随二极管两端的偏置电阻大小变化而变化,并且垂直极化和水平极化的仿真结果完全一致;在5.6~17.6 GHz范围内,整体反射率包络低于-15 dB,带宽达到12 GHz.从而得到了一种宽频段、高吸收、双极化的可调微波吸收体.
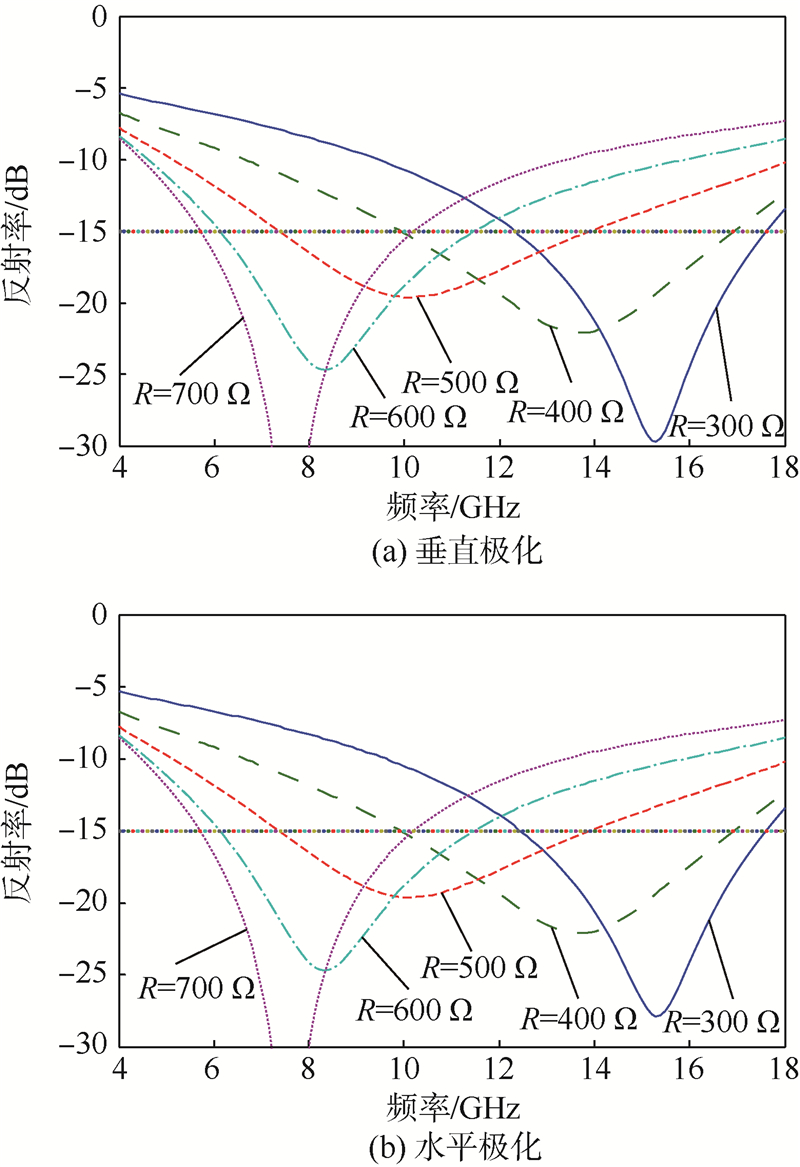 |
| 图 13 十字型可调微波吸收体优化结果Fig. 13 Optimized results of cross tunable microwave absorber |
针对传统雷达吸波材料吸波特性固定的缺点,本文设计了一种有源可调微波吸收体.实验研究表明:
1) 可调阻抗层由FSS阵列和PIN二极管组成,在FSS阵列上设计了并联馈电网络,便于使用普通的电压/电流源和电表进行调整和校正.
2) 通过改变流过PIN二极管的电流大小,可以有效控制有源可调微波吸收体的最佳吸波频率;当电流大小在0~0.5 mA变化时,该吸收体对垂直极化的入射波在7~12.5 GHz范围内实现了吸波特性的可控迁移.
3) 有源可调微波吸收体可以根据敌方雷达的威胁频率动态调整自身的吸波频率,具有智能化特点.
4) 有源可调微波吸收体在同等厚度基础上吸波带宽更大.
优化设计了具有双极化吸波特性的有源可调微波吸收体,为宽频段、高吸收、双极化的高性能吸波材料研究和开发提供了一种新途径.
| [1] | Knott E F, Shaeffer J F, Tuley M T.Radar cross section[M].2nd ed.Norwood:Artech House, 1993:156-158. |
| [2] | Fante R L.Reflection properties of the salisbury screen[J].IEEE Transactions on Antennas and Propagation, 1988, 36(10):1443-1454. |
| Click to display the text | |
| [3] | du Toit L J.The design of Jaumann absorbers[J].IEEE Antennas and Propagation Magazine, 1994, 36(6):17-25. |
| Click to display the text | |
| [4] | Munk B A.Frequency selective surfaces:Theory and design[M].New York:Wiley, 2000:15-50. |
| [5] | Rozanov K N.Ultimate thickness to bandwidth ratio of radar absorbers[J].IEEE Transaction Antennas Propagation, 2000, 48(8):1230-1234. |
| Click to display the text | |
| [6] | Chang T K, Langley R J, Parker E A.An active square loop frequency selective surface[J].IEEE Transaction Microwave and Guided Wave Letters, 1993, 3(10):387-388. |
| Click to display the text | |
| [7] | Tennant A, Chambers B.A single-layer tunable microwave absorber using an active FSS[J].IEEE Microwave and Wireless Components Letters, 2004, 14(1):46-47. |
| Cited By in Cnki Click to display the text | |
| [8] | 徐欧, 朱敏.双层方环可电控FSS吸波屏设计和实验研究[J].电波科学学报, 2009, 24(5):837-843.Xu O, Zhu M.Design and measurement of active absorber using the double layer square loop FSS[J].Chinese Journal of Radio Science, 2009, 24(5):837-843(in Chinese). |
| Cited By in Cnki (10) | |
| [9] | 高正平, 饶力.电路模拟技术在吸波结构中的应用[J].电子科技大学学报, 1998, 27(2):576-579.Gao Z P, Rao L.Circuit analog technique applied to structural absorbers[J].Journal of University of Electronic Science and Technology of China, 1998, 27(2):576-579(in Chinese). |
| Cited By in Cnki (16) | |
| [10] | 饶克谨, 赵伯琳, 高正平.电路模拟吸收材料-原理、特性及设计方法[J].电子科技大学学报, 1995, 24(2):164-170.Rao K J, Zhao B L, Gao Z P.Circuit analogue absorbing material principles, character and design[J].Journal of University of Electronic Science and Technology of China, 1995, 24(2):164-170(in Chinese). |
| Cited By in Cnki | |
| [11] | Langley R J.Equivalent circuit model for arrays of square loops[J].IEEE Transaction Electronics Letters, 1982, 18(7):294-296. |
| Click to display the text | |
| [12] | 王焕青.等效电路法分析频率选择表面的双频特性[J].系统工程与电子技术, 2008, 30(11):2054-2057.Wang H Q.Analysis of double properties of frequency selective surfaces by using equivalent circuit method[J].Systems Engineering and Electronics, 2008, 30(11):2054-2057(in Chinese). |
| Cited By in Cnki (9) | |
| [13] | Lee C K, Langley R J.Equivalent-circuit models for frequency-selective surfaces at oblique angles of incidence[J].IEEE Transaction Antennas, Microwave Circuits and Networks, 1985, 132(6):395-399. |
| Click to display the text | |
| [14] | Michalewicz Z, Krawczyk J B, Kazemi M, et al.Genetic algorithms and optimal control problem[C]∥Proceedings of 29th IEEE Conference on Decision and Control.Piscataway, NJ:IEEE Press, 1990:1664-1666. |
| [15] | Weibe D S, Michielssen E, Goldberg D H.Genetic algorithm design of Pareto optimal broad band microwave absorbers[J].IEEE Transaction Electronics Compat, 1996, 38(3):518-524. |
| Click to display the text | |
| [16] | Chambers B.Optimum design of a Salisbury screen radar absorber[J].Electronics Letters, 1994, 30(16):1353-1354. |
| Click to display the text |



