标准轨迹制导发展较早,近阶段已经出现了多种制导方法,部分已在航天飞机上成功应用,但标准轨迹制导对状态初值过于敏感,且对不确定因素的影响调节能力有限,反馈增益系数的确定方法复杂,鲁棒性较差等问题一直有待改善.近些年,标准轨迹制导的研究取得了较大进展,Mease提出了阻力加速剖面的制导方法对其进行了改进[1, 2],在保证制导精度的基础上,提高了其航程能力;雍恩米[3]通过航程预测,实现了对参考轨迹的跟踪;Ping等[4, 5]在此基础上利用简单的LQR控制律完成了轨迹跟踪;刘君等提出了一种基于广义标准轨迹的平衡滑翔状态反馈制导方法[6],在采用小倾侧角假设的前提下,实现了远程滑翔再入助推制导.目前,标准轨迹制导的研究主要集中于如何提升制导系统的鲁棒性和制导精度方面.
本文首先对模糊理论进行了介绍,对隶属度函数的建立原则进行了分析;接着对通用航空飞行器(Common Aero Vehicle,CAV)再入纵向制导进行研究,根据要求建立了隶属度函数,同时对控制律在再入制导问题中的适用性进行了分析,并仿真验证了控制律的有效性;然后对侧向制导问题进行了讨论分析,提出了改善侧向制导精度的方法;最后对本文提出的制导方案进行了仿真验证,分析了其可行性,并对主要不足进行了讨论.
1 基于模糊滑模的纵向制导律设计滑动模态控制又称变结构控制,其具有响应速度快、对参数变化及扰动不敏感、物理实现简单等优点,因此,在实际工程领域得到了较好的应用.但滑模控制存在抖振问题,成为了变结构控制在实际系统中应用的最大障碍.
模糊方法可根据经验设计模糊逻辑规则,并采用模糊逻辑实现滑模参数的自适应调整以有效降低滑模控制抖振;同时,其自身的万能逼近特性能有效逼近外界干扰及不确定性,并加以补偿,可将间断的控制信号连续化,以减轻或避免抖振现象.因此,模糊滑模控制在不确定系统及复杂外界干扰的情况中广泛适用,其在复杂非线性系统中的应用价值也得到了有力证明[7, 8].
本文将滑模控制和模糊控制结合起来,实现对再入飞行器纵向参考轨迹的最小误差跟踪.
1.1 纵向状态方程CAV纵向状态方程[9]可表示为
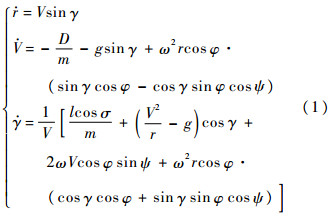
式中:r为地心距;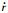 为高度的变化率;V和
为高度的变化率;V和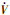 分别为飞行器的速度和加速度;γ为航迹角;r为航迹角变化率;D为阻力;m为飞行器质量;g为重力加速度;ω为角速度;φ为纬度;ψ为航向角;σ为倾侧角;l为距离.
分别为飞行器的速度和加速度;γ为航迹角;r为航迹角变化率;D为阻力;m为飞行器质量;g为重力加速度;ω为角速度;φ为纬度;ψ为航向角;σ为倾侧角;l为距离.
由于对攻角进行了参数化处理,故只将倾侧角作为控制量,对式(1)进行简化:
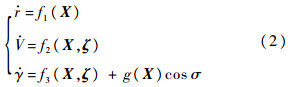
式中:
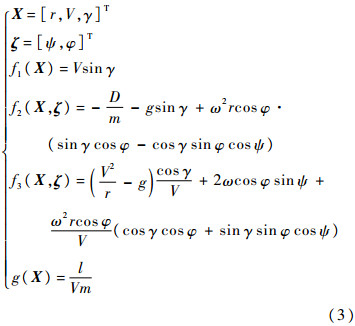
式中:X为输入.
令σ=σr+Δσ,σr为观测值,Δσ为偏差,假设Δσ在较小的范围内取值,则
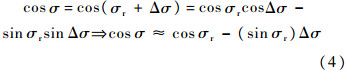
则式(2)中的 可表示为
可表示为
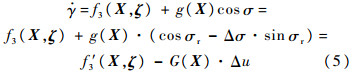
式中:
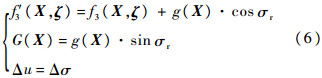
纵向平面不考虑倾侧角的符号,即有σr>0,则G(X)>0.
1.2 模糊系统设计本文的模糊系统设计主要基于零阶Takagi-Sugeno模糊系统的点模糊化方法与中心平均去模糊化方法[10].
由于X=[r,V,γ]T⊂R3,则该模糊系统有3个输入,针对每个输入分别设计3个模糊集合Ajl(j=1,2,3为模糊系统的输入,l=1,2,3为3个模糊集合的编号),可知该模糊系统总共含有27条模糊规则,第i条模糊规则可描述为:R(i):If r is A1l,V is A2l,γ is A3l,then y is Bi,i=1,2,…,27.其中,y∈v⊂R为模糊系统的输出,B=[B1,B2,…,B27]为输出的模糊形式.
为了描述输入与模糊集合的关系,本文为每个集合设计三角隶属度函数.设M(a,b;X)为三角隶属度函数,(a,b)为模糊集合边界,且b>a.当X∈(a,b)时,M(X)∈(0,1),当X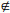 (a,b)时,M(X)=0.模糊集合Ajl的归属度可表示为
(a,b)时,M(X)=0.模糊集合Ajl的归属度可表示为

式中:ajl和bjl分别为模糊系统输入为j时模糊集合i的模糊集合边界;Xj=X(j)为参考状态变量.
利用中心平均解模糊器对模糊系统进行处理,则Takagi-Sugeno模糊系统输出[11]可表示为

式中:
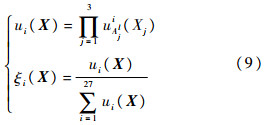
式中: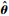 为某一变量的估计值;
为某一变量的估计值;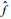 为X和
为X和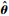 的估计函数;
的估计函数;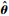 i为
i为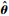 第i条模糊规则的分量;ui(X)为第i条模糊规则的归属度;ξi(X)为模糊基向量ξ(X)第i条模糊规则的分量.则模糊基向量可表示为ξ(X)=[ξ1(X),ξ2(X),…,ξ27(X)],则式(8)可表示为
第i条模糊规则的分量;ui(X)为第i条模糊规则的归属度;ξi(X)为模糊基向量ξ(X)第i条模糊规则的分量.则模糊基向量可表示为ξ(X)=[ξ1(X),ξ2(X),…,ξ27(X)],则式(8)可表示为
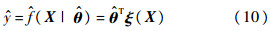
这种具有通用近似属性的经典模糊逻辑系统能够以任意精度逼近任何连续函数,本文将用其对理想控制增量进行逼近.
1.3 隶属度函数设计采用三角隶属度函数[12, 13],由于每个输入有3个模糊集合,每个模糊集合有一个三角隶属度函数与之对应,取参考输入Xr=[rr,Vr,γr]T=[X1r,X2r,X3r]T,故针对每个输入,隶属度函数uAjl(Xj)形式如图 1所示.
 |
| 图 1 三角隶属度函数示意图 Fig. 1 Triangular membership function schematic diagram |
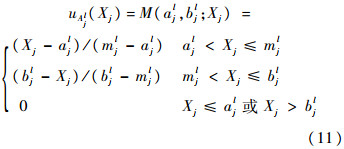
式中:
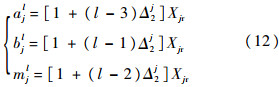
由于参考输入Xjr是时变的,为保证状态误差ej始终位于隶属度函数边界(aj1,bj3)以内,可通过实时动态调整Δ2j来获得更好的模糊逼近效果,采用如下更新规则对Δ2j进行调整,更新周期与跟踪积分步长相同.

式中:L1>1,0<L2≤1;Δ2oldj和Δj2new分别为Δj2的旧值和新值;Δj2min为Δ2j最小值,定义Δ2minj是为了防止隶属度函数边界过小甚至出现为0的情况,从而失去模糊逼近效能.考虑到γr在部分时刻可能为0,定义当|γr|≤ε(逼近误差ε为一小量)时,有
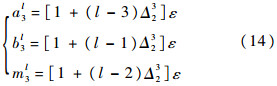
取跟踪误差为E(X)=[e1,e2,e3]T=Xr-X.定义滑模面[14, 15]为
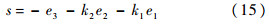
式中:k1和k2为非零正常数;e1、e2和e3为j=1,2,3时的状态误差.如果滑模控制处于理想状态,则s=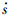 =0,即
=0,即
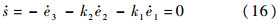
式中: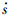 、
、 1、
1、 2和
2和 3分别为s、e1、e2和e3的导数.
3分别为s、e1、e2和e3的导数.
由式(2)及式(5)可得,式(16)可表示为
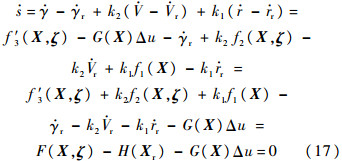
式中:
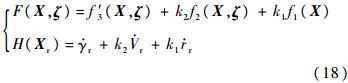
其中: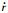 r、
r、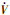 r和
r和 r分别为r、V和γ的参考值.
r分别为r、V和γ的参考值.
故Δu的理想输出Δu*应为
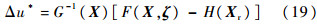
由于F(X,ζ)形式复杂,且在考虑纵向平面运动时,侧向信息为未知量,因此,Δu*难以实现,故可利用模糊系统逼近的方法,实现理想控制Δu*的逼近.设存在一个理想的最优模糊系统输出Δufz*(X|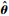 *),使得
*),使得
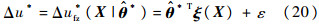
式中: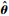 *为
*为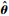 的理想值;ε满足|ε|<E.而实际模糊系统Δufz逼近Δu*应为
的理想值;ε满足|ε|<E.而实际模糊系统Δufz逼近Δu*应为
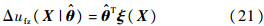
纵向状态跟踪控制律的方案设计采用误差反馈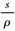 (ρ>0为一小量)来进行补偿,此时总控制律为
(ρ>0为一小量)来进行补偿,此时总控制律为

由式(20)和式(21)可得Δufz与Δu*差值为
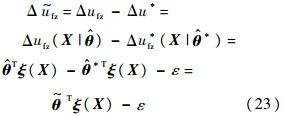
定义: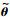 =
=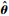 -
-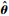 *.
*.
由式(17)和式(20)得到
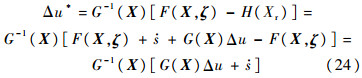
由式(22)和式(24)可知:
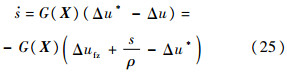
由于本文是对控制量增量Δu进行逼近,逼近误差ε最终体现在状态误差e中,而由误差反馈的特性可知,当ρ适当取值时,误差反馈对e的调节效果将远大于ε造成的e偏差[10],可认为:
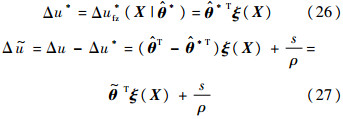
当ρ取值较大时,会弱化模糊系统对理想输出的逼近效果,由于CAV再入过程目前没有经验数据可寻,其值难以确定,目前往往采用估计的办法.
此时,定义Lyapunov函数为
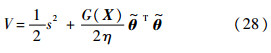
则
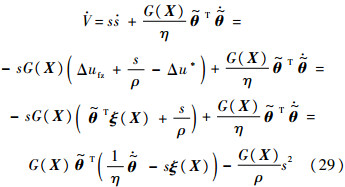
定义自适应律:
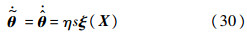
则
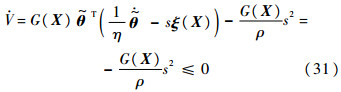
其中:η为一小量; 和
和 分别为
分别为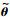 和
和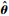 的导数.
的导数.
该方案所定义滑模系统渐进稳定. 证毕
模糊滑模制导系统结构如图 2所示.
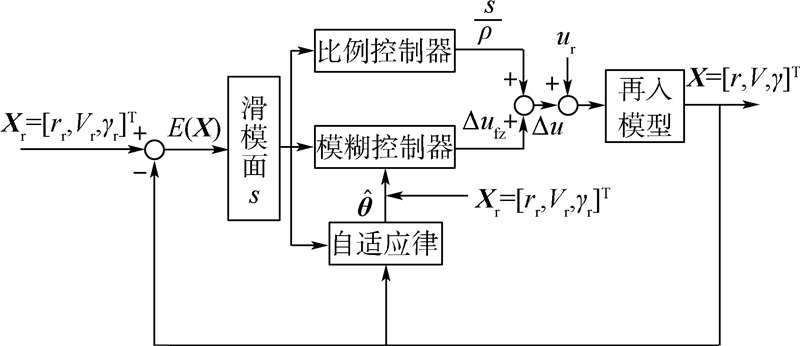 |
| 图 2 模糊滑模制导逻辑 Fig. 2 Guidance logic of fuzzy sliding mode |
由于拟平衡滑翔条件(Quasi-Equilibrium Glide Condition,QEGC)的限制,倾侧角存在上下边界,当参考倾侧角控制量与倾侧角增益叠加后,可能出现超过倾侧角边界的情况,因此,需对调整后的倾侧角控制量进行约束限制,规则为
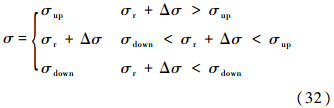
式中:σup为由拟平衡滑翔条件及过程约束决定的倾侧角上边界;σdown为QEGC决定的倾侧角下边界,定义σdown=5°.
2 侧向制导律设计 2.1 侧向状态方程CAV侧向状态方程[9]可表示为

式中:θ·为经度变化率;φ·为纬度变化率;ψ·为航向角变化率.
2.2 倾侧角反转逻辑侧向制导的重点即是确定倾侧角的反转点,目前有多种方法对反转点进行判断.其中,根据航程确定一次反转或两次反转的方法仅适用于航程较小的情况,对于大航程再入飞行,采用横程参数走廊来对反转点进行判断.
首先定义横程参数ΔZ的概念,如图 3所示.
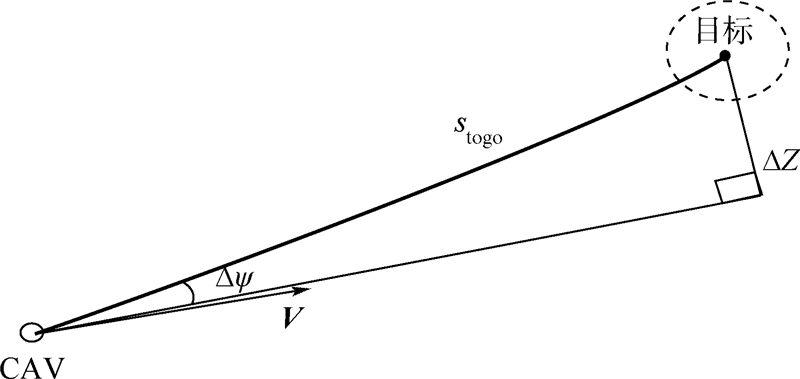 |
| 图 3 横程参数ΔZ的定义 Fig. 3 Definition of transverse process parameter ΔZ |
根据球面直角三角形的关系可知:
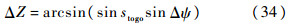
根据ΔZ的数值关系,可定义横程参数边界与剩余航程的关系为
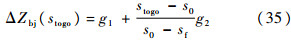
式中:g1和g2为给定参数,本文取0.2和0.19;sf为末端理想剩余航程,一般希望sf越小越好,但在实际过程中,只要求CAV到达离预定目标点一定区域即可,因此,本文取sf=0.001 6.
2.3 侧向参数反馈调节根据以往的经验,只采用倾侧角反转来实现侧向制导时,末端经纬度误差往往只能控制在2°以内,达不到制导精度要求.因此,本文利用经纬度误差小量反馈来提升末端经纬度误差精度.定义经度误差e4及纬度误差e5为
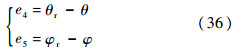
将e4和e5引入滑模面,则有
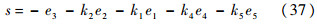
式中:k4和k5为非负常数.
由再入三维方程可知

式中:X=[r,V,γ,θ,φ]T,故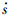 亦可表示成式(17)的形式,根据第1.5节中对稳定性的证明可知,加入经纬度误差作为总控制律时,滑模系统仍然稳定.对于模糊系统来说,如果把经纬度当作输入,则系统的模糊规则将达到243条,模糊逻辑的维数将大大增加,这将严重影响制导系统的指令解算速度,造成制导跟踪的精度大大降低.因此,本文不把经纬度作为模糊系统的输入,仍采用之前的3个输入来生成模糊输出逼近倾侧角增益,并对k4、k5做适当处理,使经纬度误差对滑模面的影响比其他参数误差小一个数量级,这样相当于e4、e5对倾侧角增益的调整为一适当小量,形成一个小的误差反馈.由于此5个状态参数之间存在较强的耦合关系,把e4、e5引入反馈后会降低其他3个变量的制导精度,但只要选取合适的k4、k5,就能把末端误差限制在一个可以接受的范围内,同时,大大降低末端经纬度的误差.对k4、k5的动态确定规则为
亦可表示成式(17)的形式,根据第1.5节中对稳定性的证明可知,加入经纬度误差作为总控制律时,滑模系统仍然稳定.对于模糊系统来说,如果把经纬度当作输入,则系统的模糊规则将达到243条,模糊逻辑的维数将大大增加,这将严重影响制导系统的指令解算速度,造成制导跟踪的精度大大降低.因此,本文不把经纬度作为模糊系统的输入,仍采用之前的3个输入来生成模糊输出逼近倾侧角增益,并对k4、k5做适当处理,使经纬度误差对滑模面的影响比其他参数误差小一个数量级,这样相当于e4、e5对倾侧角增益的调整为一适当小量,形成一个小的误差反馈.由于此5个状态参数之间存在较强的耦合关系,把e4、e5引入反馈后会降低其他3个变量的制导精度,但只要选取合适的k4、k5,就能把末端误差限制在一个可以接受的范围内,同时,大大降低末端经纬度的误差.对k4、k5的动态确定规则为

式中:kimax根据经验确定,本文取k4max=0.2,k5max=0.15.
2.4 攻角调整为了消除倾侧角反转时的误差,同时增强系统对气动参数的鲁棒性,对攻角引入微小调整量[1]:
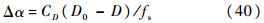
式中:fs为气动误差的函数;CD为阻力系数;D为与飞行器速度反向的阻力;D0为初始条件下的阻力.令
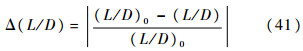
式中:L为与飞行器速度方向垂直的升力;(L/D)0、(L/D)和Δ(L/D)分别的初始条件下、当前条件下的L/D和L/D的变化量.
则
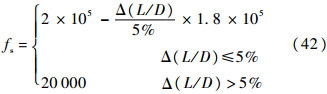
生成参考轨迹的仿真的初始条件和末端条件如表 1和表 2所示,针对本文所设计的纵向制导律,对其纵向状态进行跟踪.由于初始下降段大气稀薄,且时间较短,因此,本文从CAV进入准平滑段开始制导.整个制导过程对CAV全状态方程进行积分,积分步长为1 s,仿真初始条件,如表 1所示.
| 变量 | V0/(m·s-1) | γ0/(°) | ψ0/(°) | h0/km | θ0/(°) | φ0/(°) |
| 数值 | 7 100 | 0 | 65 | 81 | 0 | 0 |
| 注:下标0代表初始条件. | ||||||
| 变量 | Vf/(m·s-1) | hf/km | θf/(°) | φf/(°) | Δs/km |
| 数值 | 1 800 | 20 | 75 | 20 | ≤50 |
| 注:下标f代表末端条件;Δs为s的变化量. | |||||
与此同时,在仿真过程中对升力系数进行+5%的调整.仿真中各参数取值可根据各状态量数量级及相关经验确定,本文中各参数值为:k1=5×10-7,k2=8×10-5,ρ=0.01,η=20,Δ2 min=[10-5,10-3,10-2].
纵向跟踪仿真结果如图 4所示.图 4(a)为该制导方式下的再入轨迹,由图可知,制导轨迹满足再入过程约束,且拟平滑段初期轨迹波动较小;结合图 4(b)、图 4(c)可以看出,再入过程开始后500 s左右即实现了对参考轨迹的稳定跟踪,此时修正初始误差的时间更短,只用了300 s,利用误差反馈来对逼近误差及初始误差进行补偿时,其误差消除的效果要比采用切换函数时来得更快,这是由于在初始阶段误差较大,误差反馈的调节效果更加明显;从图 4(d)倾侧角的变化情况可以看出,制导初期,倾侧角调节量Δσ的值已经超出了允许边界,这说明当误差较大时,误差反馈的调节起到了主要作用,在一定程度上减弱了模糊输出的逼近效果,当误差减小到一定程度后,模糊逼近效果开始占主导作用,误差反馈到后期只起到了消除逼近误差的作用,因此,利用该方法进行制导时,相当于使模糊逼近与误差反馈发挥了互补作用,即利用模糊逼近来增加系统的自适应性,利用误差反馈来提升其控制效率.
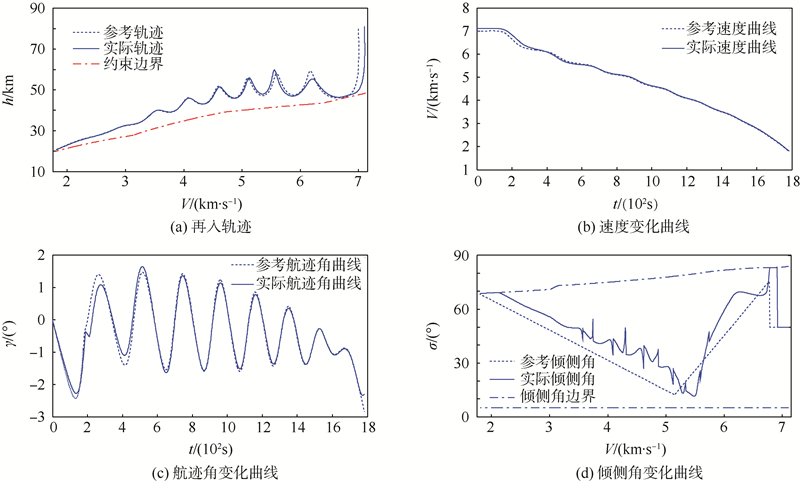 |
| 图 4 纵向跟踪仿真结果 Fig. 4 Simulation results for longitudinal tracking |
表 3为制导末端误差.可以看出,末端误差在可接受的范围内,制导效果整体较好.末端航迹角误差较大是由于倾侧角边界限制造成.
| 末端误差 | Δhf/m | ΔVf/(m·s-1) | Δγf/(°) |
| 数值 | -39.27 | -7.61 | 0.25 |
| 注:Δhf,ΔVf,Δγf—h、V和γ的末端误差. | |||
由于再入过程中气动参数的变化较为剧烈,因此气动参数误差对再入制导影响较大.为讨论该方法对气动误差鲁棒性,令初始条件无偏差,在改变气动参数情况下对系统进行仿真,不同气动偏差下末端误差的仿真结果如表 4所示.
| 气动偏差(CL/CD)/% | Δhf/m | ΔVf/(m·s-1) | Δγf/(°) |
| +2 | -27.63 | -6.67 | -0.041 |
| +5 | -79.85 | -7.84 | -0.075 |
| +10 | -76.57 | -10.68 | -0.095 |
| -2 | 38.74 | 1.06 | 0.005 |
| -5 | 57.74 | -6.37 | 0.080 |
| -10 | 98.50 | -7.64 | 0.136 |
由表 4可以看出,该方法对气动误差的鲁棒性较强,其制导性能总体较为稳定,特别是在气动偏差较大时,其对参考轨迹的跟踪误差较小,模糊逼近与误差反馈的互补性能发挥较好.
3.2 对初始误差鲁棒性仿真仍然选取第3.1节中的参考轨迹作为参考.首先对本文所设计的制导方法进行初始误差的鲁棒性仿真.在气动参数不变的条件下,改变初始条件,对跟踪效果检验,仿真结果如表 5所示.
| 初始参数变化 | Δhf/km | ΔVf/(m·s-1) | Δθf/(°) | Δφf/(°) |
| V0+100 m/s | 0.042 | -16.69 | -0.045 4 | -0.066 1 |
| V0-100 m/s | 0.101 | -4.68 | -0.093 1 | 0.081 4 |
| h0+1 km | 0.082 | -2.94 | 0.096 1 | 0.060 3 |
| h0-1 km | 0.086 | -2.77 | 0.099 6 | 0.049 5 |
| ψ0+2° | 0.061 | -5.28 | 0.041 0 | 0.160 7 |
| ψ0-2° | 0.079 | -4.84 | 0.068 5 | 0.120 9 |
| γ0+0.5° | 0.005 | -12.46 | -0.075 9 | 0.098 9 |
| γ0-0.5° | 0.099 | -3.41 | 0.108 1 | 0.080 7 |
| θ0+1° | 0.062 | 8.46 | 0.141 4 | 0.076 1 |
| θ0-1° | 0.040 | -9.06 | -0.128 5 | 0.022 6 |
| φ0+1° | 0.046 | -3.96 | 0.041 3 | 0.191 1 |
| φ0-1° | 0.096 | -3.61 | 0.069 4 | 0.137 9 |
| 注:Δθf—θ的末端误差. | ||||
由表 5中数据可以看出,该制导方法对不同初始误差的鲁棒性较好,对高度-速度剖面跟踪效果较为准确,且末端经纬度误差始终保持在0.2°以内,相对于一般的标准轨迹制导有了较大的提高.通过末端误差的比较可以看出,该制导方法对初始速度、高度误差的鲁棒性能要优于初始经纬度误差,且对于航向角或航迹角初始误差,都有比较好的跟踪效果.
图 5为不同初始偏差所得的仿真结果图,图 5中不同线代表多次仿真的结果.从图 5(a)、图 5(b)可以看出,该制导方法对高度、速度的跟踪效果较好,制导后期的误差很小.图 5(c)为不同初始条件下的地面轨迹,从中可以看出,由于采用了横程参数边界作为倾侧角反转条件,在初始条件不同的情况下,实际地面轨迹与参考地面轨迹之间存在一定的偏差,但后期经纬度误差逐渐缩小,并在末端达到一定精度,证明了本文所采用的侧向制导方案及经纬度误差小量反馈调节的方法是可行的.图 5(d)为攻角变化情况,由于引入的是微小调整量,因此,攻角的变化并不明显,其只起到对倾侧角反转时所造成的小量误差进行微调的作用.图 5(e)为倾侧角变化情况,可以看出,倾侧角主要是在再入初期进行较大的调整,到了后期跟踪误差越来越小,其变化情况趋于平缓,且整个过程中没有出现抖动的情况,因此,此模糊滑模制导方案具有较强的适应性.同时,由于所需制导参数较少且容易获得,本方案总体计算量较小,整个过程仿真时间不到30 s,对机载计算机的性能及储存空间要求不高.
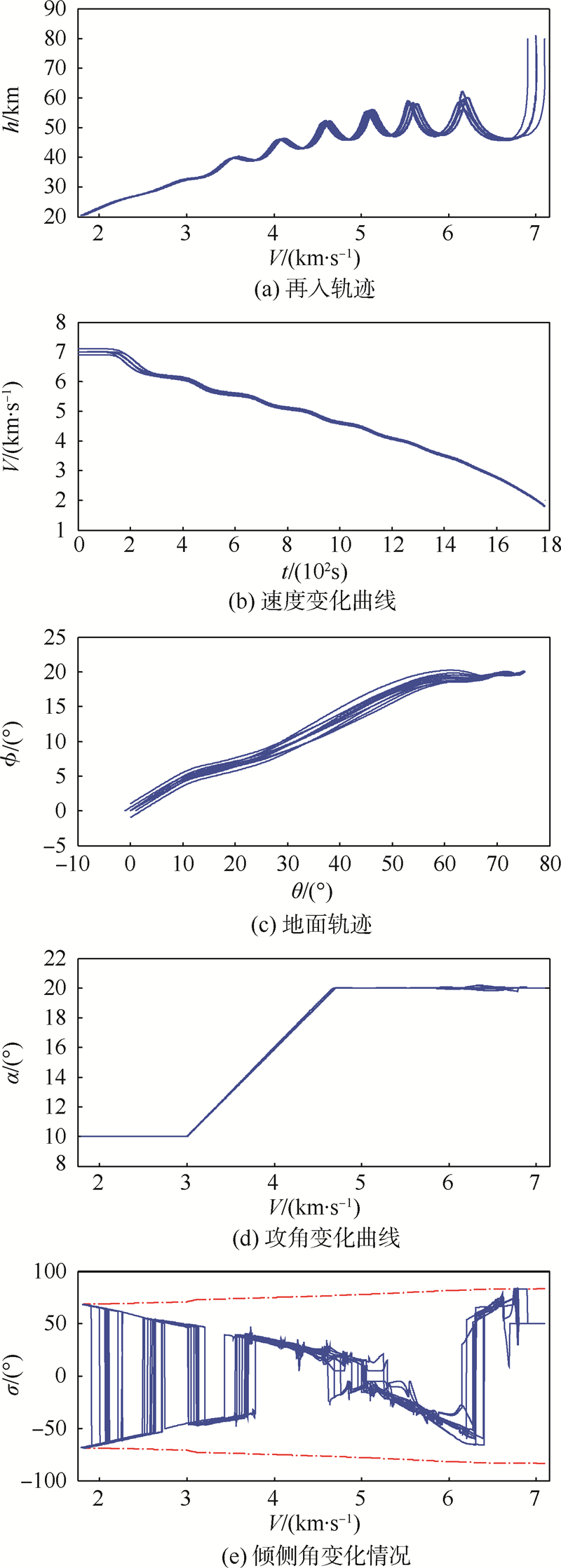 |
| 图 5 不同初始偏差所得仿真结果 Fig. 5 Simulation results for different initial deviation |
在存在气动误差的情况下对再入过程进行仿真,主要讨论当升力系数CL与阻力系数CD变化时对制导性能的影响.取CL、CD的变化范围为±15%,在此变化范围内随机取16组CL、CD的变化组合,对制导系统进行仿真,仿真结果如图 6所示.
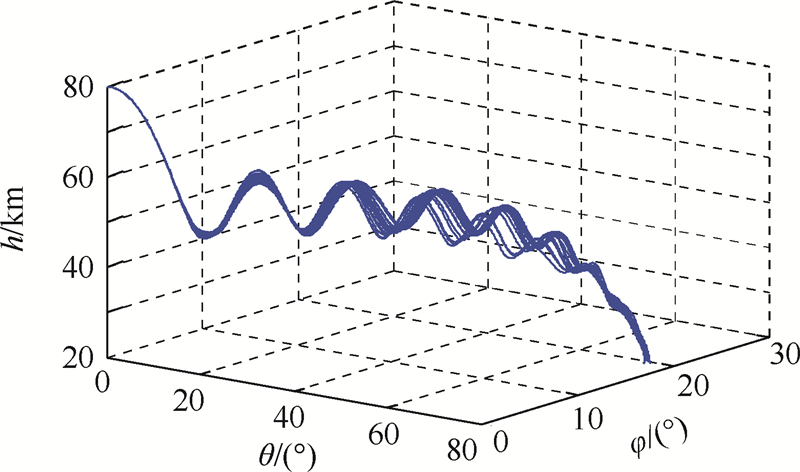 |
| 图 6 不同气动误差条件下的三维再入轨迹 Fig. 6 Three dimensions reentry trajectory in different pneumatic error |
图 6为16组不同气动误差组合的三维再入轨迹.由图 6可知,仿真末端高度均在20 km左右,误差很小,且轨迹在高度方向上重合度较高,再入过程中CAV跳跃振荡幅度几乎一致,对标准轨迹的跟踪效果较好.
图 7分别展示了16次仿真结果的终端误差.图 7(a)为终端经纬度误差,由图可以看出,末端经度误差在-0.1°~0.15°之间,而末端纬度误差大约在±0.2°之间,最大误差为距目标大约0.22°点的位置上,换算成地表距离大约为24 km.图 7(b)为末端高度速度误差,可以看出,速度误差始终在很小的范围以内,而高度误差相较于之前对初始条件误差的仿真有较大幅度的增大,但其误差始终在±0.3 km之内,可以很好地满足末端精度的要求,鲁棒性较强.
 |
| 图 7 16次仿真结果的终端误差 Fig. 7 Terminal errors of 16 times of simulation |
另外,本文利用横程参数边界决定倾侧角反转作为侧向制导逻辑,根据横程误差的定义及边界设定,可以使航向角误差在制导末端保持在很小的范围内;而整个模糊滑模制导过程是在实现对航迹角跟踪的基础上进行的,航迹角误差几乎可以忽略不计.因此,整个过程的航迹角与航向角误差都在很小的范围内变化,不会对CAV后续的任务执行产生影响.
4 结 论本文对CAV再入标准轨迹制导问题进行了研究,利用模糊滑模实现了在线制导,主要研究工作和相关结论为:
1) 针对CAV纵向再入模型,设计了模糊滑模系统,并对控制律进行稳定性分析,通过仿真发现在利用模糊滑模系统对标准轨迹进行跟踪时,利用模糊逼近与误差反馈相结合的方式能够使实际轨迹更快地实现对标准轨迹的跟踪,且对气动误差的鲁棒性很强.
2) 在纵向制导律的基础上进行了侧向制导律设计,利用倾侧角反转逻辑与侧向参数反馈调节相结合的方式,设计了三维标准轨迹制导方案,同时,针对倾侧角反转过程中产生的微小误差,采用攻角调整的方式进行补偿.
3) 对本文所设计的模糊滑模制导律进行了仿真验证,仿真结果证实了本文所设计的基于模糊滑模的标准轨迹制导方案能够满足末端精度要求,且对各种误差的鲁棒性较强,具有实际应用价值.
| [1] | Mease K D.Reduced-order entry trajectory planning for acceleration guidance[J].Journal of Guidance,Control and Dynamics,2002,25(2):257-266. |
| Click to display the text | |
| [2] | Mease K D.Design and evaluation of an acceleration guidance algorithm for entry[J].Journal of Guidance,Control and Dynamics,2004,41(6):986-996. |
| Click to display the text | |
| [3] | 雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙:国防科技大学,2008. Yong E M.Study of hypersonic glide-reentry vehicle for trajectory optimization and guidance method[D].Changsha:National University of Defense Technology,2008(in Chinese) |
| Cited By in Cnki (18) | |
| [4] | Shen Z J,Ping L.Dynamic lateral entry guidance logic[J].Journal of Guidance,Control and Dynamics,2004,27(6):949-959. |
| Click to display the text | |
| [5] | Zuo J S,Ping L.On-board generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control,and Dynamics,2003,26(1):111-121. |
| Click to display the text | |
| [6] | 刘君,陈克俊,汤国建.基于广义标准轨迹的平衡滑翔状态反馈制导方法[J].国防科技大学学报,2012,34(2):134-140. Liu J,Chen K J,Tang G J.Equilibrium glide for state feedback guidance method based on generalized standard trajactory[J].Journal of National University of Defense Technology,2012,34(2):134-140(in Chinese). |
| Cited By in Cnki | |
| [7] | Yaghmaee M H,Menhaj M B,Safavi M.A novel FLC-based approach for ATM traffic control[J].Computer Networks,2011,36(5-6):643-658. |
| Click to display the text | |
| [8] | Wu S F,Engelen C J H,Babuska R,et al.Fuzzy logic based full envelope autonomous flight control for an atmospheric re-entry spacecraft[J].Control Engineering Practice,2003,11(1):11-25. |
| Click to display the text | |
| [9] | 国海峰,黄长强,丁达理,等.考虑随机干扰的高超声速滑翔飞行器轨迹优化[J].北京航空航天大学学报,2014,40(9):1281-1290. Guo H F,Huang C Q,Ding D L,et al.Trajectory optimization for hypersonic gliding vehicle considering stochastic disturbance[J].Journal of Beijng University of Aeronautics and Astronautics,2014,40(9):1281-1290(in Chinese). |
| Cited By in Cnki | |
| [10] | Ghasemi A,Moradi M,Menhaj M B.Adaptive fuzzy sliding mode control design for a low-lift reentry vehicle[J].Journal of Aerospace Engineering,2012,25(2):210-216. |
| Click to display the text | |
| [11] | 刘金琨.滑模变结构控制[M].北京:清华大学出版社,2012:110-116. Liu J K.Sliding mode control design[M].Beijing:Tsinghua University Press,2012:110-116(in Chinese). |
| [12] | 张化光,何希勤.模糊自适应控制理论及其应用[M].北京:北京航空航天大学出版社,2002:56-60. Zhang H G,He X Q.Fuzzy adaptive control theory and application[M].Beijing:Beihang University Press,2002:56-60(in Chinese). |
| [13] | 席爱民.模糊控制技术[M].西安:西安电子科技大学出版社,2008:120-128. Xi A M.Technology of fuzzy control[M].Xi'an:Press of Xidian University,2008:120-128(in Chinese). |
| [14] | 赵霞,姜玉宪,吴云洁,等.基于多模态滑模的快速非奇异终端滑模控制[J].北京航空航天大学学报,2011,37(1):110-113. Zhao X,Jiang Y X,Wu Y J,et al.Fast nonsingular terminal sliding mode control based on multi slide mode[J].Journal of Beijng University of Aeronautics and Astronautics,2011,37(1):110-113(in Chinese). |
| Cited By in Cnki (3) | |
| [15] | 李菁菁,任章,沈振.高超声速滑翔飞行器的分散鲁棒姿态控制[J].北京航空航天大学学报,2012,38(9):1194-1199. Li J J,Ren Z,Shen Z.Design of decentralized robust attitude controller for hypersonic sliding vehicles[J].Journal of Beijng University of Aeronautics and Astronautics,2012,38(9):1194-1199(in Chinese). |
| Cited By in Cnki |



