平衡滑翔的概念最早由Sanger提出,指的是纵向受力近似平衡的一种飞行状态.平衡滑翔是再入的一种重要飞行模式[1],具有高度变化平缓、热流密度和动压峰值小、攻角和倾侧角曲线光滑等优点,被广泛地应用于再入制导[2, 3].
由于再入弹道对控制变量高度敏感,在弹道优化时往往难以获得平衡滑翔弹道[4, 5],同时再入过程中的各种扰动也容易使得弹道偏离平衡滑翔状态,从而出现弹道振荡.因此,为了使高超声速飞行器在再入过程中保持平衡滑翔,不仅需要获得平衡滑翔参考弹道,还需在飞行过程中抑制扰动带来的弹道振荡.
在航天飞机再入制导律中,Harpold和Graves[2]采用阻力速度曲线来规划平衡滑翔参考弹道,并通过配置阻力动态系统的自然频率和阻尼来跟踪阻力曲线.平衡滑翔条件是研究平衡滑翔问题的重要假设,它通过忽略平衡滑翔弹道倾角变化率的影响,将纵向运动微分方程转化为了代数方程.Bell[6]利用该条件获得了平衡滑翔再入弹道的解析解;Chapman,Wingrove和Etkin[7, 8, 9]则利用平衡滑翔条件分析了再入弹道的动态特性,并提出以高度差及高度一阶导数差的负反馈来抑制弹道振荡;Shen和Lu[10]则利用平衡滑翔条件将再入高度走廊转化成为了倾侧角走廊;Yu和Chen[11]则分析了给定攻角和倾侧角曲线的平衡滑翔弹道倾角; 乔清青和陈万春[12]则在此基础上采用奇异摄动法获得了滑翔段的最优中制导.尽管平衡滑翔条件在分析平衡滑翔弹道的特性上取得了很多的成果,但它并不能积分获得平衡滑翔参考弹道,这是由于实际的再入弹道倾角并非常数.Zhang和Chen[13]在改进的平衡滑翔条件中,加入了坡度率的影响,通过规划坡度率来获得平衡滑翔弹道,但它获得的攻角曲线变化范围较大.
本文在传统平衡滑翔概念的基础上,通过分析给定攻角曲线和倾侧角曲线再入弹道族的特点,提出以纵向加速度导数的平方的积分来衡量弹道的平滑程度,并以此为基础定义了平稳滑翔弹道.然后对平稳滑翔弹道的解析解和弹道动态特性进行了分析,从而获得了快速生成平稳滑翔弹道的方法.
1 动力学模型
为了便于理论分析,假设地球为非旋转均质圆球,则再入纵向动力学方程为
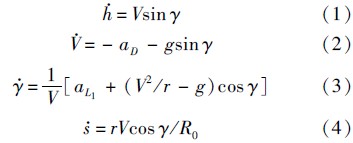
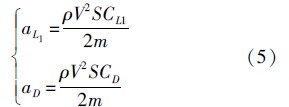

另外,选用洛马公司的通用航空飞行器方案CAV-H[13]作为仿真校验飞行器模型,该飞行器最大升阻比可达3.5,质量为907 kg,气动参考面积为0.483 9 m2.为了便于计算,进一步对升力系数和阻力系数拟合[13]得到:
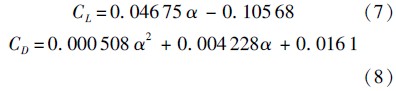
2 平稳滑翔弹道的提出 2.1 平稳滑翔弹道定义
在进行滑翔弹道规划时,规划变量通常为攻角α和倾侧角σ,对应着纵向升力系数CL1和阻力系数CD.对于给定的连续可导的纵向升力系数曲线C*L1和阻力系数曲线C*D,所得滑翔弹道的振荡幅度与初始状态相关,当初始状态取值合适时,可能获得无振荡的平滑弹道,不同初始状态下的滑翔弹道如图 1所示.
 |
| 图 1 不同初始状态下的滑翔弹道(α=15°,σ=0°) Fig. 1 Glide trajectories with different initial states (α=15°,σ=0°) |
为了获得最为平滑的再入弹道,分别选取表 1中的目标函数.
采用SQP(Sequential Quadratic Programming)法对初始高度和弹道倾角进行搜索,得到的不同目标函数下的滑翔弹道如图 2所示.由图可以看出,采用目标函数1,获得的高度曲线相对平滑,但弹道倾角曲线存在小幅振荡;采用目标函数2,获得高度曲线和弹道倾角曲线均相对平滑,但纵向加速度曲线存在小幅振荡;而采用目标函数3,则能使得上述三者均为平滑曲线.
因此,可定义目标函数3所获得的再入弹道为平稳滑翔弹道.
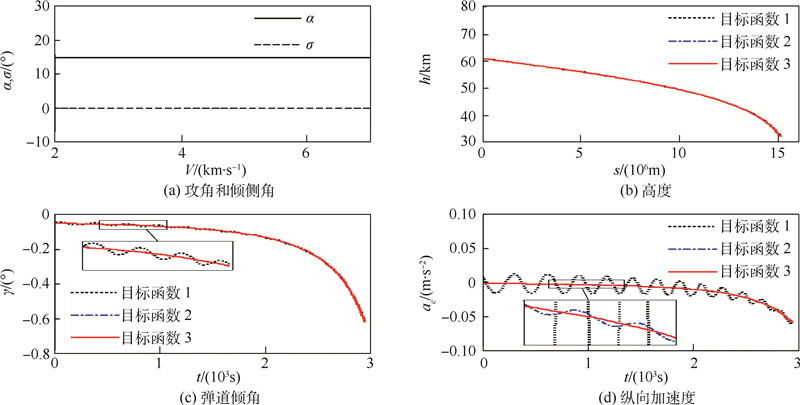 |
| 图 2 不同目标函数下的滑翔弹道 Fig. 2 Glide trajectories under different cost functions |
2.2 控制特性对平稳滑翔弹道的影响
当且仅当再入弹道的攻角曲线和倾侧角曲线均连续可导时,才能获得对应的平稳滑翔弹道,不连续或者不可导的攻角曲线(或者倾侧角曲线)均只能得到振荡的再入弹道,攻角曲线连续性对平稳滑翔弹道的影响如图 3所示.
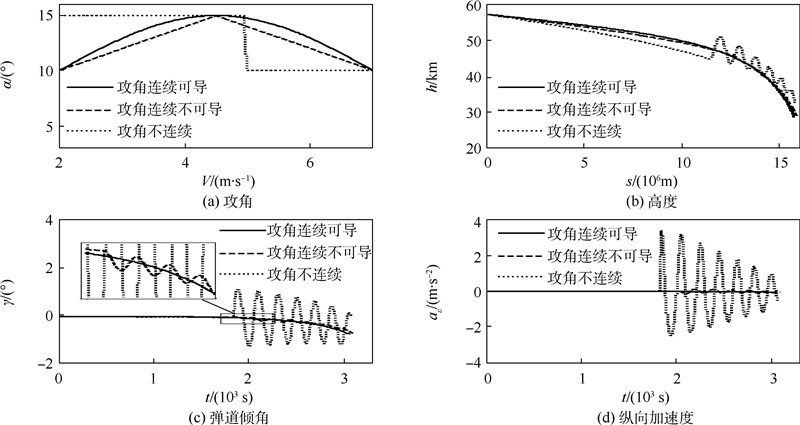 |
| 图 3 攻角曲线连续性对平稳滑翔弹道的影响(σ=0°) Fig. 3 Effect of angle of attack curve continuity on steady glide trajectories (σ=0°) |
平稳滑翔弹道要求初始高度和弹道倾角等于特定值.当初始高度或者初始弹道倾角取值不满足要求时,所获得的弹道会围绕平稳滑翔弹道振荡.
图 4给出了不同h0时滑翔弹道的高度偏差Δh 和弹道倾角偏差Δγ.图 4中α=15°,σ=0°;Δh=h-hsg,Δγ=γ-γsg,hsg和γsg分别为平稳滑翔高度及弹道倾角.
由图 4可以看出,Δh和Δγ均在零附近振荡,并且振幅逐渐减小.
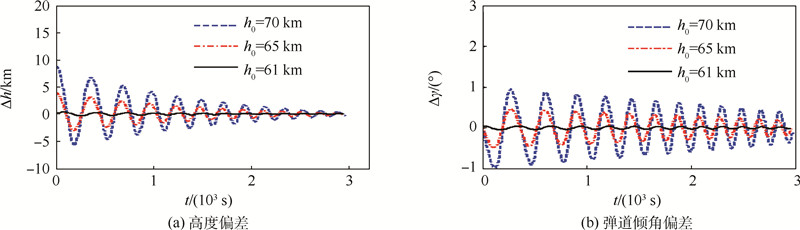 |
| 图 4 不同h0时滑翔弹道的高度偏差和弹道倾角偏差 Fig. 4 Height deviation and flight path angle deviation of glide trajectory with different h0 |
式(1)给出了高度对时间的一阶导数,将其对时间进一步求导,并代入式(2)和式(3),可得
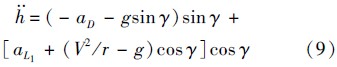
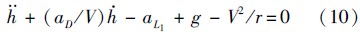
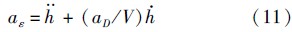
设fK = C*D/C*L1为纵向升阻比的倒数,则阻力加速度可写为

将式(5)和式(12)代入式(10)可得
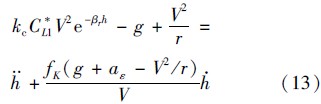
3.2 基于正则摄动的平稳滑翔高度解析解
为了实现对平稳滑翔弹道的快速规划,需要对平稳滑翔弹道的高度、弹道倾角和纵向加速度进行解析求解.由图 2和图 3可知,平稳滑翔弹道的纵向加速度aε为小量,因此可采用平衡滑翔条件来估算平稳滑翔弹道的高度.平衡滑翔条件假定aε=0,其表达式为
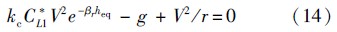
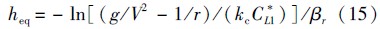
然而,由于平衡滑翔条件忽略了aε的影响,使得平衡滑翔高度与平稳滑翔高度之间存在一定的偏差,如图 5所示(图中Δheq=heq-hsg).可以看出当速度较大时,两者之差较小,采用式(15)估算平稳滑翔高度具有较高的精度;当速度较小时,两者之差较大,采用式(15)估算平稳滑翔高度精度较差.
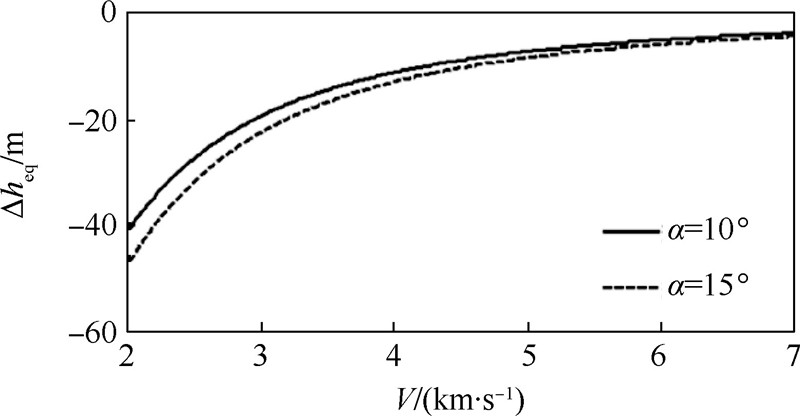 |
| 图 5 平衡滑翔高度与平稳滑翔高度之差 Fig. 5 Difference between equilibrium glide heights and steady glide heights |
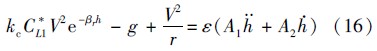


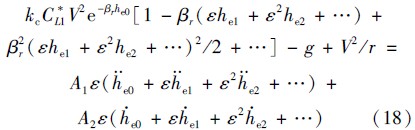
由式(18)可得,平稳滑翔高度的零阶项即为平衡滑翔高度,即he0=heq,一阶项和二阶项则分别满足:
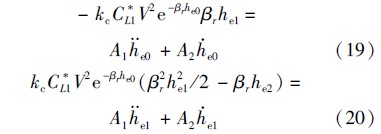
3.2.1 高度一阶项
将he0对时间求一阶导数可得
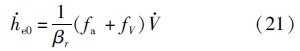
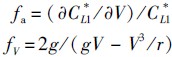
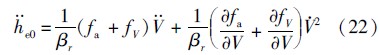
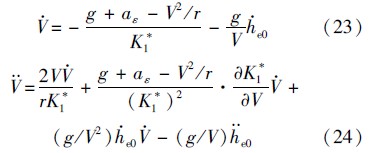
将式(14)、式(21)和式(22)代入式(19),可得高度的一阶项为
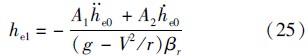
将he1分别对时间求一阶导数和二阶导数,并代入式(20),可得高度的二阶项为
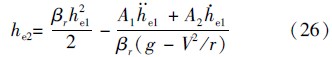
图 6给出了不同阶数的平稳滑翔高度解析解与数值方法获得的平稳滑翔高度之间的误差(仿真攻角为15°,倾侧角为0°).由图可知,仅考虑高度零阶项时,解析解与数值解之间的最大误差可达40 m;在考虑一阶项后,最大误差降低到1 m左右;但二阶项仅使最大误差减小0.2 m;因此,在实际应用时可只考虑到高度一阶项.
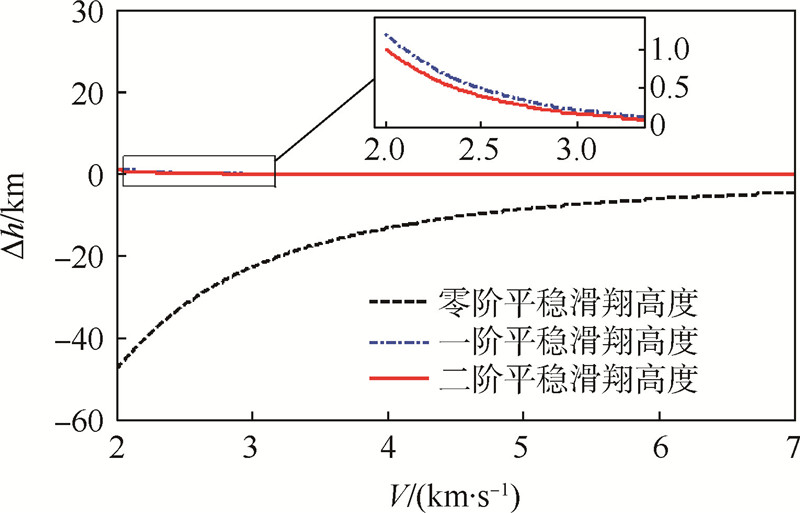 |
| 图 6 不同阶数平稳滑翔高度解析解精度 Fig. 6 Accuracy of steady glide height analytical solutions in different orders |
通过对平稳滑翔高度解析解求导,可获得平稳滑翔弹道倾角和纵向加速度的解析解:
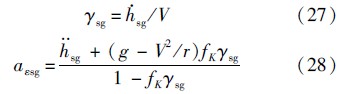
式中:γsg和aεsg分别为平稳滑翔弹道倾角和纵向加速度;hsg和hsg分别为平稳滑翔高度的一阶导数和二阶导数:
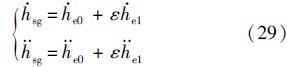
在式(27)和式(28)中,若C*L1和fK保持不变,并忽略gsin γ和aεsg对V的影响,则γsg和aεsg可简化为
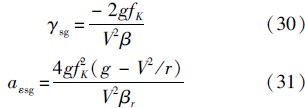
图 7为平稳滑翔弹道倾角和纵向加速度的解.图 7(a)和图 7(b)分别给出了平稳滑翔弹道倾角和纵向加速度的解析解和数值解,图 7中仿真算例的攻角曲线和倾侧角曲线表达式如表 2所示.可以看出,攻角和倾侧角的解析解均与数值解非常接近,均随速度的增大而增大,其中平稳滑翔弹道倾角解析解的相对误差小于1%,而平稳滑翔纵向加速度解析解的相对误差则小于2%.
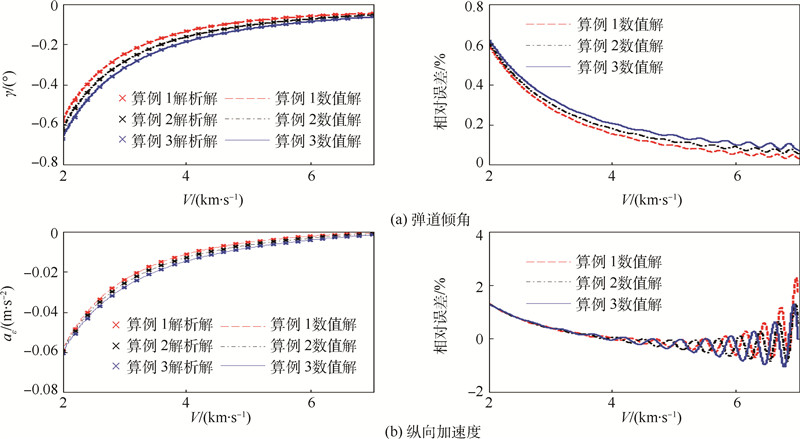 |
| 图 7 平稳滑翔弹道倾角和纵向加速度的解 Fig. 7 Solutions of steady glide flight path angle and longitudinal acceleration |
| 算例 | 攻角/(°) | 倾侧角/(°) |
| 1 | α=17-0.001 V | σ=0 |
| 2 | α=15 | σ=0 |
| 3 | α=8+0.001 V | σ=0 |
| 4 | α=15+5sin[0.000 8 π(V-2 000)] | σ=0 |
在文献[14]和文献[11]中,Ferreira和Yu等 分别给出了平衡滑翔弹道倾角的解析解,图 8将它们与本文结果(式(27))进行了对比.图 8中Δγ为解析解与数值方法获得的平稳滑翔弹道倾角之差.由图 8可以看出,Ferreira的结果与数值解的差异最大,特别是在攻角变化的情况下(算例1和算例3),这是由于Ferreira忽略了气动系数变化的影响;文献[11]和本文结果均与数值解的差异较小,但本文精度更高,这是由于Yu和Chen在推导解析解的过程中假定aε=0.
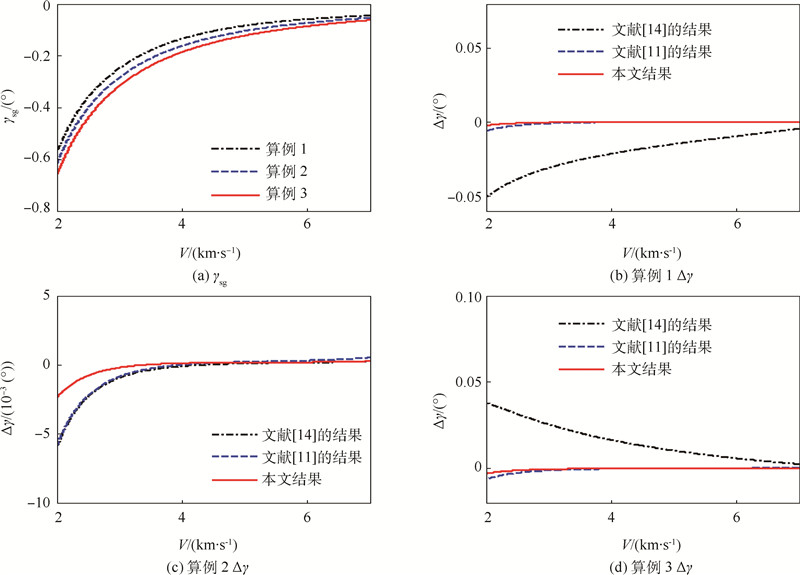 |
| 图 8 不同方法获得的平稳滑翔弹道倾角解析解精度对比 Fig. 8 Comparison of accuracy for different analytical solutions of steady glide flight path angle obtained by different methods |
4.1 稳定性分析
为了获得平稳滑的翔弹道,飞行高度和弹道倾角必须分别满足式(17)和式(27),然而实际再入过程中滑翔段的起始高度和弹道倾角很可能不满足上述关系,并且飞行过程中扰动也会使弹道偏离平稳滑翔状态,从而使得弹道振荡(如图 1所示).
通过分析Δh,可获得平稳滑翔弹道的动态特性.将第2.3节Δh定义代入式(10)可得
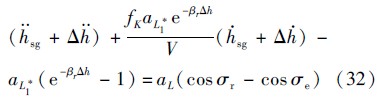
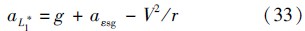

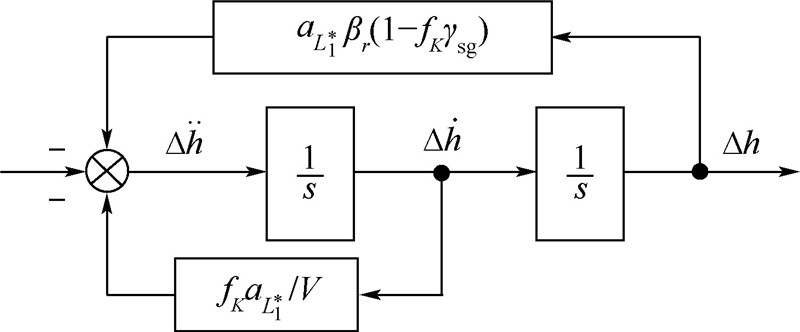 |
| 图 9 Δh的动态系统结构 Fig. 9 Dynamic system structure of Δh |
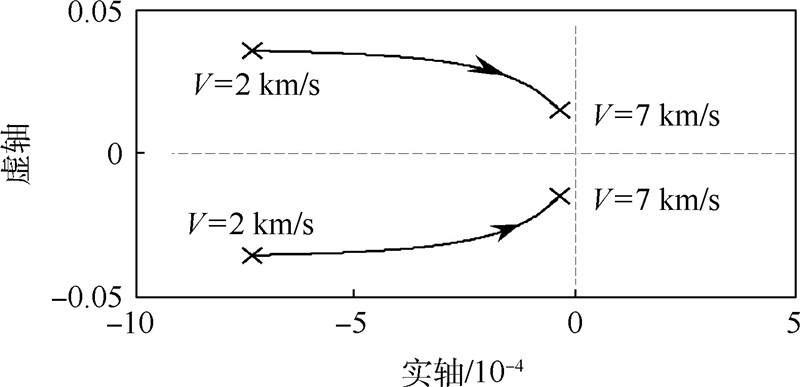 |
| 图 10 参数V的根轨迹 Fig. 10 Root locus of parameter V |
利用式(34),可得平稳滑翔高度增量振荡的 自然频率ωn和阻尼ζ分别为

将式(33)代入式(35)和式(36),并忽略aεsg和γsg等小量的影响,可得
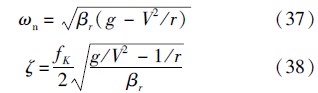
由式(37)和式(38)可知,平稳滑翔高度增量振荡的自然频率仅与当前的飞行速度相关,而阻尼则与速度及纵向升阻比相关.
图 11给出了不同h0(算例2)下的平稳滑翔高度偏差的自然频率.可以看出,两者对自然频率的影响均非常小,实际弹道仿真获得的自然频率与式(38)给出的解析结果几乎完全重合.图 12则分析了攻角的变化对自然频率的影响,可以看出它对自然频率的影响很小.图 13进一步将本文结果与Harpold和Graves[2]在航天飞机再入制导律中获得的再入弹道振荡自然频率解析解进行了对比,可以看出两者几乎完全重合,均与实际弹道高度增量的振荡频率相吻合,但本文给出的结论更为简洁.
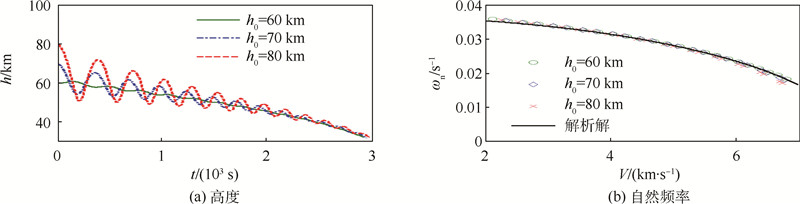 |
| 图 11 初始高度对自然频率的影响(定攻角) Fig. 11 Impact of initial heights on natural frequency (fixed angle of attack) |
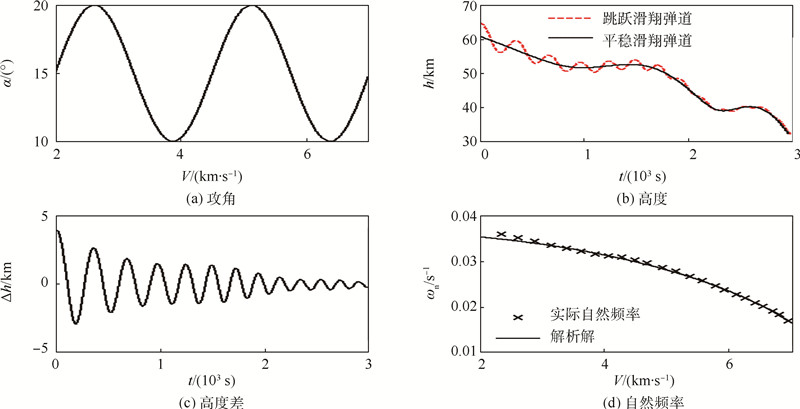 |
| 图 12 攻角变化对自然频率的影响 Fig. 12 Impact of angle of attack change on natural frequency |
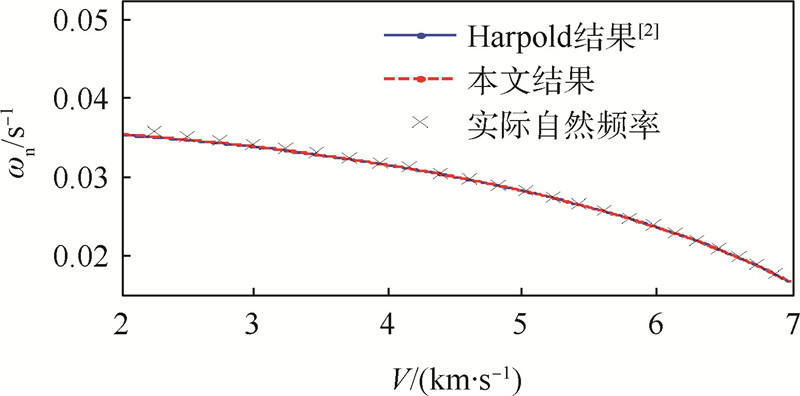 |
| 图 13 不同方法获得的自然频率 Fig. 13 Natural frequencies obtained by different methods |
图 14给出了阻尼及高度曲线,由于无法从弹道获得阻尼大小,因此只能进行定性分析.由图可以看出,相同攻角下,倾侧角越大,则对应弹道的高度振荡收敛越快,说明阻尼越大,与式(38)给出的结论相符.
 |
| 图 14 阻尼及高度曲线 Fig. 14 Damping and height curves |
5.1 反馈系数选取
由于再入弹道的阻尼非常小,使得弹道在偏离平稳滑翔时弹道振荡不易收敛.为了使振荡的弹道快速收敛到平稳滑翔状态,需要对平稳滑翔高度增量动态系统的极点进行配置.
在传统的再入跟踪制导律中,通常采用比例反馈(Δh或者ΔD)和微分反馈(Δh或者Δγ)来配置系统的极点,将它们引入平稳滑翔高度增量动态系统后,动态方程变为
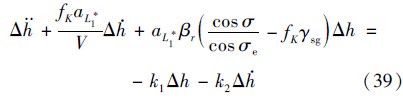
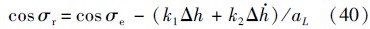
图 15给出了k1和k2对式(39)给出的平稳滑翔高度增量动态系统参数根轨迹的影响.可以看出,改变k1会使根轨迹上下移动,主要影响系统的自然频率;改变k2则使得根轨迹左右移动,主要影响系统的阻尼.由图 15(a)可知,在k1=0时,改变k2也能使根轨迹明显远离虚轴,能够明显改变系统的阻尼;由图 15(b)可知,增大k1会降低k2的调节效率;由图 15(c)和图 15(d)可以看出,改变k1不会改变根轨迹与虚轴的相对位置,反而会减小系统的阻尼.
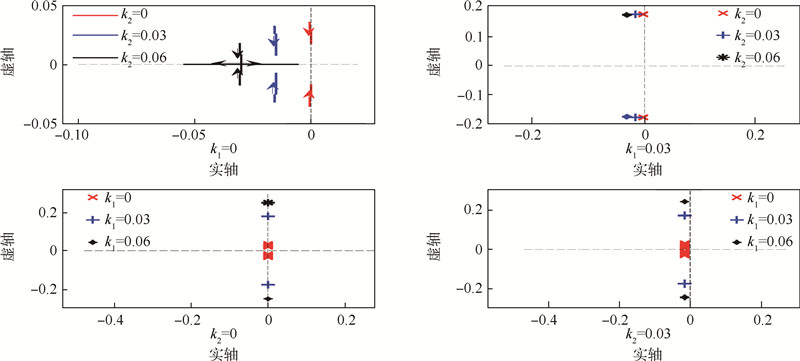 |
| 图 15 k1和k2对参数根轨迹的影响 Fig. 15 Impact of k1and k2 on parameter root locus |
图 16比较了k1Δh和k2Δh所对应的反馈量(加速度增量Δa),可以看出k2Δh要远远小于k1Δh.图 17和图 18给出了不同反馈系数下的仿真结果.可以看出,在倾侧反转(小扰动)下,弹道会在平稳滑翔高度附近振荡.由图 17和图 18可知,当k2=0时,高度差几乎不收敛,并且倾侧角振 荡厉害;而当k2=0.03时,高度差快速收敛到零,倾侧角也快速收敛到期望值.图 19则进一步分析了k1的影响,由图可以看出,k1取0和0.001时,弹道的收敛速度几乎一致,但k1=0对应的倾侧角的变化更为平缓.
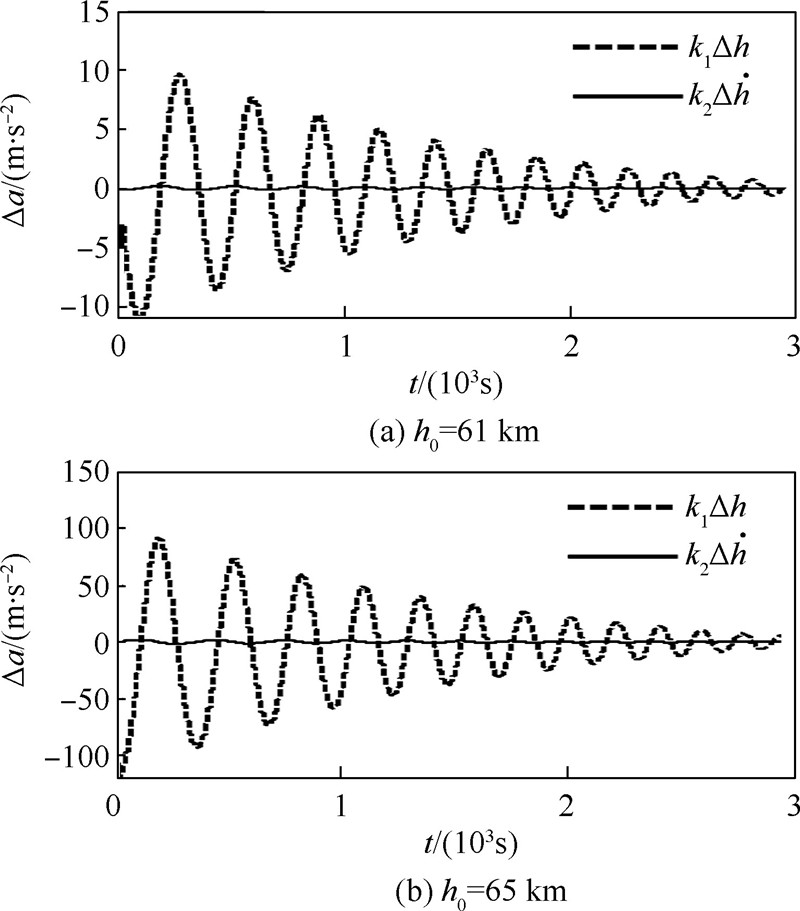 |
| 图 16 比例反馈和微分反馈的比较 Fig. 16 Comparison of proportional feedback and differential feedback |
 |
| 图 17 反馈系数对Δh的影响(小扰动) Fig. 17 Impact of feedback coefficients on Δh (small perturbation) |
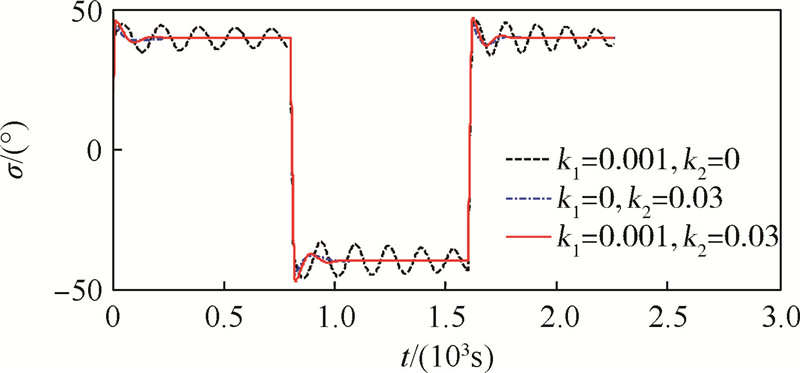 |
| 图 18 反馈系数对倾侧角的影响(小扰动) Fig. 18 Impact of the feedback coefficients on bank angles (small perturbation) |
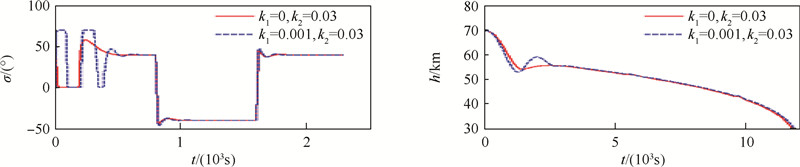 |
| 图 19 k1的影响分析(大扰动) Fig. 19 Analysis of impact of k1 (large perturbation) |
总的来说,比例反馈并不能加快振荡弹道的收敛,却需要较大的反馈量.因此在再入弹道跟踪时可仅采用微分反馈来抑制弹道振荡.该方案又称为弹道阻尼控制,最早由Phillips[15]提出,被用于制导炮弹的增程制导律;Yu和Chen[11]将其引入再入弹道规划,并给出了最大升阻比对应的平稳滑翔弹道倾角;徐明亮等[16]则将其应用于高升阻比飞行器的再入预测制导律;本文则在上述研究之上进一步夯实了弹道阻尼控制的理论基础.
5.2 定阻尼微分反馈系数
当再入高度增量动态系统的阻尼为0.4~0.8时,系统的调节时间较短、超调量较小.但对于给定的k2,系统的阻尼随速度变化较大,因此需要根据当前速度实时调整反馈系数.设阻尼取定值,则反馈系数为
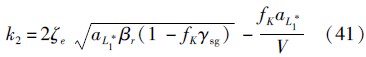
将式(41)代入式(40),即可获得抑制弹道振荡所需的倾侧角.若由式(40)获得的倾侧角超出其可行范围,则需要通过调整攻角来获得所需要的反馈加速度.
图 20给出了存在初始状态偏差情况下采用定阻尼微分反馈获得的滑翔段弹道,图中stogo为剩余射程.可以看出,不论初始状态如何,在定阻尼微分反馈的作用下,弹道均快速收敛到平稳滑翔状态.
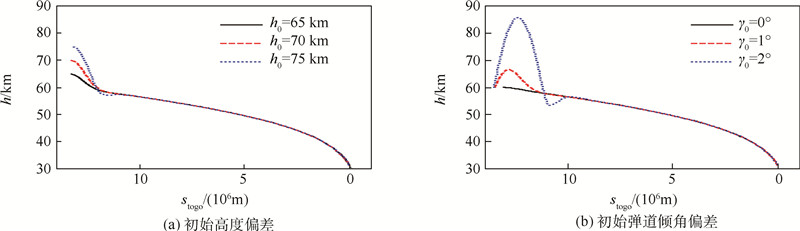 |
| 图 20 存在初始状态偏差的平稳滑翔弹道 Fig. 20 Steady glide trajectories with initial state errors |
图 21为引入段的攻角曲线、弹道曲线及热流密度dQ曲线.图 21(a)~图 21(c)将定阻尼微分反馈应用于引入段制导,图中引入段的起点和终点的速度、高度和弹道倾角均给定,其中伪谱法以引入段射程最大为目标函数.由图 21(a)可知,采用定阻尼微分反馈方法获得攻角曲线较为光滑,并且在引入段的高度快速下降阶段保持攻角最大,这样能最大限度地降低引入段的最大热流密度(见图 21(c)).由图 21(b)可知,采用定阻尼微分反馈方法获得的引入段弹道更为光滑,但射程略微小于伪谱法结果.
 |
| 图 21 引入段的攻角曲线、弹道曲线及热流密度曲线 Fig. 21 Angle of attack histories,trajectories and heating rate histories of initial descent phase |
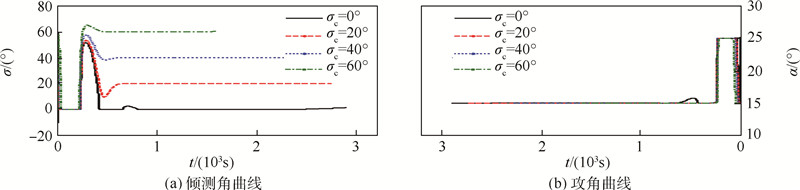 |
| 图 22 倾侧角曲线和攻角曲线 Fig. 22 Bank angle histories and angle of attack histories |
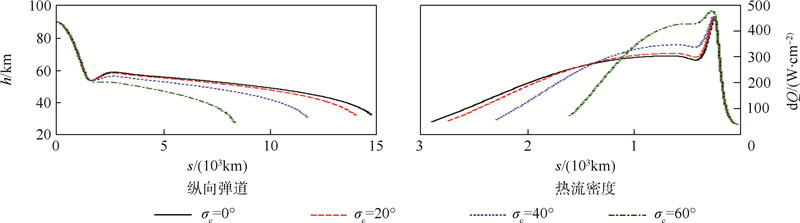 |
| 图 23 再入弹道曲线和热流密度曲线 Fig. 23 Reenty trajectories and heating rate histories |
本文研究了高超声速飞行器平稳滑翔问题,得到:
1) 对于给定的攻角和倾侧角,提出以纵向加速度变化率平方的积分为衡量弹道平滑性的指标,并定义该指标取极小值时的弹道为平稳滑翔弹道.平稳滑翔弹道是所有相同攻角和倾侧角再入弹道族的中心,其余弹道均围绕它振荡.
2) 建立了平稳滑翔高度动态微分方程,并采用正则摄动的方法求解获得了平稳滑翔弹道高度、弹道倾角和纵向加速度的解析解,利用解析解可快速获得期望升力系数和阻力系数对应的平稳滑翔弹道.
3) 平稳滑翔弹道具有自然稳定性和弱阻尼性.其自然频率仅与当前的飞行速度相关,而阻尼则还与纵向升阻比成反比.
4) 对于再入滑翔弹道,比例反馈并不能使弹道振荡收敛,却需要较大的反馈量;而微分反馈则能使振荡的弹道快速收敛到平稳滑翔状态,同时所需要的反馈量较小,因此纯微分反馈是抑制再入滑翔弹道振荡的最佳方案.
5) 定阻尼微分反馈不仅适用于滑翔段的纵向弹道控制,还可用于引入段弹道的生成,简化了再入滑翔弹道的纵平面制导.
| [1] | 陈小庆,侯中喜, 刘建霞.高超声速滑翔飞行器弹道特性分析[J].导弹与航天运载技术,2011,312(2):5-9. Chen X Q,Hou Z X,Liu J X.Trajectory characteristic of hypersonic gliding vehicle[J].Missiles and Space Vehicles,2011,312(2):5-9(in Chinese). |
| Cited By in Cnki | |
| [2] | Harpold J C, Graves C A.Shuttle entry guidance[J].The Journal of the Astronautical Sciences,1979,37(3):239-268. |
| Click to display the text | |
| [3] | Mease K D, Chen D T,Sch nenberger H.Reduced-order entry trajectory planning for acceleration guidance[J].Journal of Guidance,Control and Dynamics,2002,25(2):257-266. |
| Click to display the text | |
| [4] | 周浩,陈万春, 殷兴良.高超声速飞行器滑行航迹优化[J].北京航空航天大学学报,2006,32(5):513-517. Zhou H,Chen W C,Yin X L.Optimization of glide trajectory for a hypersonic vehicle[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(5):513-517(in Chinese). |
| Cited By in Cnki (44) | |
| [5] | Jorris T R, Cobb R G.Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J].Journal of Guidance,Control and Dynamics,2009,32(2):551-572. |
| Click to display the text | |
| [6] | Bell B N. A closed-form solution to lifting reentry,AFFDL-TR-65-65[R].Ohio:AFFDL,1965. |
| [7] | Chapman D R. An approximate analytical method for studying entry into planetary atmospheres,NASA-TR-R-11[R].Washington,D.C.:NASA,1959. |
| Click to display the text | |
| [8] | Wingrove R C. A study of guidance to reference trajectories for lifting re-entry at supercircular velocity,NASA-TR-151[R].Washington,D.C.:NASA,1963. |
| Click to display the text | |
| [9] | Etkin B. Longitudinal dynamics of a lifting vehicle in orbital flight[J].Journal of the Aerospace Science,1961,28(2):779-788. |
| Click to display the text | |
| [10] | Shen Z, Lu P.Onboard generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control and Dynamics,2003,26(1):111-121. |
| Click to display the text | |
| [11] | Yu W, Chen W.Guidance scheme for glide range maximization of a hypersonic vehicle,AIAA-2011-6714[R].Reston:AIAA,2011. |
| Click to display the text | |
| [12] | 乔清青,陈万春. 高超声速导弹近最优中制导律[J].飞行力学,2014,32(1):48-52. Qiao Q Q,Chen W C.Near-optimal midcourse guidance law for hypersonic missile[J].Flight Dynamics,2014,32(1):48-52(in Chinese). |
| Cited By in Cnki (0) | |
| [13] | Zhang K, Chen W.Reentry vehicle constrained trajectory optimization,AIAA-2011-2231[R].Reston:AIAA,2011. |
| Click to display the text | |
| [14] | Ferreira L O. Nonlinear dynamics and stability of hypersonic reentry vehicles[D].Michigan:University of Michigan,1995. |
| Click to display the text | |
| [15] | Phillips C A. Guidance algorithm for range maximization and time-of-flight control of a guided projectile[J].Journal of Guidance,Control and Dynamics,2008,31(5):1447-1455. |
| Click to display the text | |
| [16] | 徐明亮,陈克俊, 刘鲁华,等.高超声速飞行器准平衡滑翔自适应制导方法[J].中国科学:技术科学,2012,42(4):378-387. Xu M L,Chen K J,Liu L H,et al.Quasi-equilibrium glide adaptive guidance for hypersonic vehicles[J].Scientia Sinica Technologica,2012,42(4):378-387(in Chinese). |
| Cited By in Cnki (1) |




