2. 北京航空航天大学 飞行器控制一体化技术重点实验室, 北京 100191;
3. 北京航天自动控制研究所, 北京 100854
2. Science and Technology on Aircraft Control Laboratory, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
3. Beijing Aerospace Automatic Control Institute, Beijing 100854, China
轨迹线性化控制(Trajectory Linearization Control,TLC)是Zhu等在20世纪90年代中后期逐步建立并发展起来的一种有效新颖的非线性跟踪和解耦控制方法[1, 2, 3].由于其具有特定的控制结构(开环前馈求伪逆+闭环反馈调节跟踪误差),使得系统输出沿着标称轨迹指数稳定,从而保证了TLC具有一定的鲁棒性和较强的抗干扰能力,目前已被成功应用于空天飞行器[1, 2]以及机器人控制[3]等系统.但文献[4]研究发现,当系统中不确定性增大至一定程度,TLC的控制性能将会遭到破坏甚至失效.因此,针对TLC方法的弊端,如何改善或提高TLC的控制性能及抗干扰能力成为了近年来的热点研究问题[5, 6, 7, 8, 9].目前针对该问题所采取的解决思路可归纳如下:基于“观测+补偿”的思想,利用神经网络[5, 6, 7, 8]或者模糊逻辑[9]对不确定性因素的良好逼近能力,来抵消不确定性对系统的影响.因此研究内容主要集中在补偿器的设计、引入补偿器后复合系统的稳定性分析与证明等方面.其中Liu等[5]针对一类非线性系统,研究了基于自适应神经网络的TLC控制方法,提高了闭环系统的鲁棒性.朱亮等[6]针对近空间飞行器的姿控问题,研究了基于单隐层神经网络(Single Hidden Layer Neural Network,SHLNN)的直接自适应TLC控制方法,文献[7]在文献[6]的基础上研究了一种新的鲁棒自适应TLC控制策略,可以降低文献[6]中控制器设计时的保守性,避免了因参数选取不当导致过高的控制增益等问题.类似地,薛雅丽等[8]提出了基于RBFNN(Radal Basis Function Neural Network)的TLC控制方法,可有效解决存在气动参数摄动时飞行器的强鲁棒姿控问题.Jiang等[9]针对一类非线性系统,研究了基于T-S(Takagi-Sugeno)模糊系统的鲁棒自适应TLC控制方法.然而,在上述文献中,基于神经网络理论设计的补偿器调参较复杂,且模糊系统中规则的构造等都需要一些先验知识作支撑,这都无疑增加了设计过程的复杂度.因此如何引入某种新的设计思路且紧密结合TLC方法的理论框架,寻求出一种设计上更简洁,具有强抗干扰特性的控制方法成为了亟需解决的新问题.
另一方面,对于非线性跟踪微分器的研究是目前的一大热点研究问题,韩京清和袁露林[10]给出了跟踪微分器(Tracking Differentiator,TD)的设计及证明过程,取代了原有的差分方法,并将其应用于各种控制系统[11].王新华等[12]提出的全程快速跟踪微分器(或称混合微分器)在信号滤噪与求导方面具有明显优势,并且系统状态具有在远离和接近平衡点都能自动以较快速度收敛、跟踪速度快和无抖振等特点[12],文献[13]设计了一种基于奇异摄动技术的有限时间收敛微分器(Finite Time Convergence Differentiator,FTCD)算法(严格讲,FTCD是混合微分器的特殊形式),文献[14]设计了基于FTCD的滑模变结构控制律,仿真实验和实测数据证实了该微分器具有较强的抑制噪声能力[14].
本文受非线性跟踪微分器设计思路的启发,并立足于TLC方法的理论框架,尝试将微分器的特性合理融入TLC方法的设计过程中,以改善TLC的控制性能,并将该方法在高超声速飞行器的姿控系统中得到了验证.
考虑如下非线性动态系统:
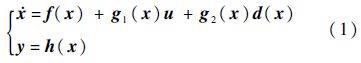
式中:x∈Rn×1、u∈Rn×1、y∈Rn×1分别为系统的状态、输入和输出;f(x)、g1(x)、g2(x)、h(x)为适当维数的光滑有界函数;d(x)∈Rn×1表示未建模误差和外界干扰的总和,并且满足假设1.
假设1 对于所有的x∈Rn×1,必存在非线性函数g0(x)且满足g0(x)g1(x)=g2(x),其中存在正的有界实数σ使得||g2(x)||≤σ成立.
首先,令d(x)=0,根据TLC的设计思想,标称状态x、标称输入u以及标称输出y满足:
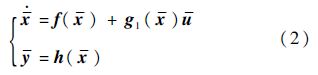
定义x=x+e,u=u+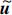 ,则闭环系统跟踪误差动态特性方程为
,则闭环系统跟踪误差动态特性方程为
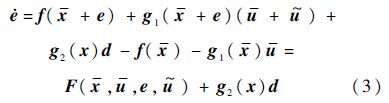
考虑式(3)中x和u可视为系统的时变参数,故式(3)可简记为
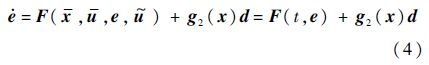
考虑如下线性时变系统:
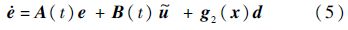
式中:
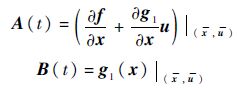
式(4)和式(5)分别满足假设2和假设3.
假设2 当d=0时,e=0为式(5)的孤立平衡点,F:[0,∞)×De→Rn,De={e∈Rn|||e|| <Re}连续可微,雅克比矩阵[∂F/∂t]关于t一致有界,在De上满足Lipschitz条件.其中De为误差e的定义域;Re为误差e可选取的实数集.
假设3 线性时变系统式(5)中A(t)和B(t)对于所有允许的参数值满足:①关于t光滑有界且有连续有界的n-1次微分;②{A(t),B(t)}一致完全可控,那么存在控制律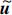 =K(t)e使得当d=0时线性时变系统式(5)在原点处指数稳定.
=K(t)e使得当d=0时线性时变系统式(5)在原点处指数稳定.
换句话说,系统状态在控制律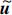 和u的共同作用下以指数形式收敛于期望的标称轨迹状态.不妨记Ac(t)=A(t)+B(t)K(t),其中Ac(t)为待设计的矩阵,根据文献[1, 2, 3]可采用PD谱理论设计保证系统赫尔维茨稳定.
和u的共同作用下以指数形式收敛于期望的标称轨迹状态.不妨记Ac(t)=A(t)+B(t)K(t),其中Ac(t)为待设计的矩阵,根据文献[1, 2, 3]可采用PD谱理论设计保证系统赫尔维茨稳定.
根据TLC方法的设计思想和步骤,标称输出可由式(2)推导得出(仅讨论MIMO系统相对阶为1的情况,即h(x)=x):
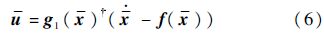
式中:符号†表示伪逆运算符,其计算表达式为A†=AT(AAT)-1.为了保证系统的因果性,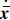 将由x经过伪微分器求得
将由x经过伪微分器求得
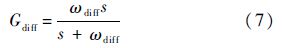
式中:ωdiff为伪微分器Gdiff的带宽.
可见伪微分器中时间常数T=1/wdiff越小,微分的近似程度越高,通常为保证控制品质,指令信号v(t)需经过一阶惯性环节平滑后得到x,最后送入上述伪微分器中获取微分信号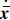 ,这里不失一般性,令一阶惯性环节的时间常数为T,则指令信号v(t)至
,这里不失一般性,令一阶惯性环节的时间常数为T,则指令信号v(t)至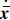 的传递函数为
的传递函数为
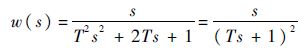
其状态变量实现为
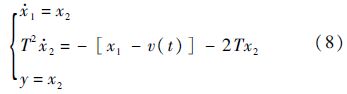
可得
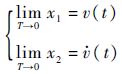
其形式等价于二阶线性积分链式微分器[15],并且T等效于摄动参数ε,当式(8)的状态初始值与v(0)有较大误差时,由于微分器的高增益影响,使得初始时刻附近,微分器的导数估计会存在峰值现象.故T足够小时微分信号近似程度较高的同时,过渡阶段会引起标称指令的微分信号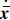 乃至标称输入u的剧烈跳变,可见该峰值现象是当前TLC方法无法避免的.
乃至标称输入u的剧烈跳变,可见该峰值现象是当前TLC方法无法避免的.
现考虑如下二阶积分串联系统:
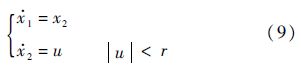
式中:r为系统实际能提供的最大控制量.
双积分串联系统对应的二阶离散系统为
z2(k+1)=z2(k)+hu(k) |u(k)|≤r
定理1 对于形如式(9)的串联系统,在满足加速度限制|x1| <r的条件下,以任意有界可积信号v(t)为终点的快速最优控制综合函数为
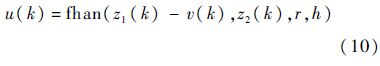
由式(9)和式(10)构成的动态系统具有如下性质:
1) 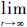 ∫0T|x1(r,t)-v(t)|=0,x1(r,t) 的导数x2(r,t)弱收敛于函数v(t)的广义导数.
∫0T|x1(r,t)-v(t)|=0,x1(r,t) 的导数x2(r,t)弱收敛于函数v(t)的广义导数.
2) 若输入信号为单位阶跃信号且幅值为v,T0为阶跃响应过渡过程的时间,则过渡过程时间T0与最大加速度r满足:
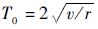
且
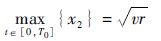
定理1详细证明过程可参见文献[16],这里不再赘述.由定理1可知二阶韩氏跟踪微分器[16]具有根据系统输入能力事先安排过渡过程的优点,并且能够保证过渡过程的快速性且无超调,此外过渡过程的微分信号的峰值可通过最大加速度r来调节,可有效抑制初始阶段线性微分器中的峰值现象.因此这里引入二阶最速离散跟踪微分器[16]替换TLC方法中的一阶惯性+伪微分器环节,跟踪微分器具体形式为
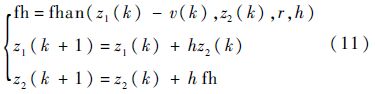
式中:fhan(z1(k)-v(k),z2(k),r,h)[16]为二阶最速离散跟踪微分器输入;h为积分步长;跟踪微分器的输出z1(k)即为安排的过渡过程信号;z2(k)为过渡信号z1(k)的微分信号.
2.2 线性时变系统(LTV)跟踪误差调节器的改进现考虑无扰系统式(5)(d=0),为消除静差,将式(5)的状态向量增广成PI(Proportional Integral)形式,有

此时式(5)可改写成:
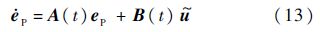
记e=[eI eP]T,由式(12)和式(13)构成新的跟踪误差动态方程,写成矩阵形式:
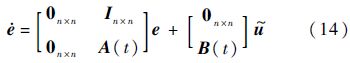
定理2 针对形如式(14)的非线性系统,选择控制器为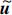 =B(t)†(-KIeI-KPeP-A(t)eP)可以保证闭环跟踪误差e在原点处指数收敛,其中KI和KP为适维的正定对角矩阵.
=B(t)†(-KIeI-KPeP-A(t)eP)可以保证闭环跟踪误差e在原点处指数收敛,其中KI和KP为适维的正定对角矩阵.
证明 为保证式(14)跟踪误差指数收敛,则式(15)必恒成立:
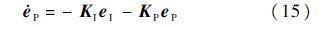
式(15)为期望的误差动态特性方程.
两边同时求导取Laplace变换,有
式中:kP,i和kI,i为KP和KI对角线上相应的元素,且满足s2+kP,is+kI,i=0是Hurwitz的,这里不失一般性,kP,i和kI,i满足:
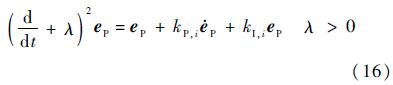
再由A(t)eP+B(t)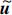 =-KIeI-KPeP可直接推导出控制律
=-KIeI-KPeP可直接推导出控制律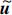 .证毕
.证毕
定理2通过构造跟踪误差特性方程为切入点,间接求出了控制律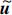 ,与改进前TLC方法(先将线性时变(Linear Time-varying,LTV)系统转换为可控标准型,然后根据PD谱理论求得状态反馈矩阵,最后得到控制律
,与改进前TLC方法(先将线性时变(Linear Time-varying,LTV)系统转换为可控标准型,然后根据PD谱理论求得状态反馈矩阵,最后得到控制律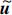 )相比,这种处理方式规避了TLC方法中线性时变系统一致完全可控的限制,换句话说,即使假设3不成立,通过定理2依然可以获得控制律
)相比,这种处理方式规避了TLC方法中线性时变系统一致完全可控的限制,换句话说,即使假设3不成立,通过定理2依然可以获得控制律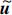 .
.
以上讨论的是无扰情况下LTV的控制律求解问题,接下来,以提高TLC的控制性能及抗干扰能力为出发点着重讨论受扰情况下式(5)的控制律的设计.首先给出关于混合微分器的引理:
引理1[12] 如下所示系统:
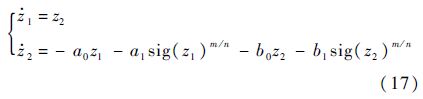
式中:sig(y)a=|y|asgn(y),a>0,如果a0、a1、b0、b1>0、m和n均为大于0的奇数,且m <n,那么系统式(17)在原点是渐近稳定的,即满足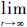 z1=0及
z1=0及 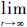 z2=0.
z2=0.
详细的证明过程参见文献[12].
推论1[12] 引理1所述的混合微分器在系统状态远离和接近平衡点时都能自动以较快速度收敛,远离时线性环节起主导作用,接近时非线性环节起主导作用,使得系统状态始终保持快速收敛性,系统式(17)实际上可分为2个阶段:
1) 当|z|>1时,由于m <n,有|z|>|zm/n|,所以系统状态在远离平衡点时,|z|远大于|zm/n|,系统式(14)中起主导作用的形式为
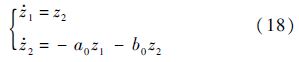
易证系统(18)仍然是渐进稳定的,且保持较快的收敛速度,其收敛速度与z1、z2值的绝对值成正比.
2) 当|z| <1时,由于m <n,有|z|<zm/n|,所以系统状态接近于平衡点时,z远小于zm/n,系统式(14)中起主导作用的形式为
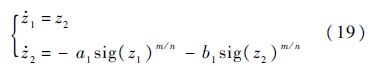
形如式(19)的系统称为非线性微分器,由文献[17]的证明可知其相对于原点是有限时间收敛的,并且保持快速收敛性.
不难发现,定理2所述的系统期望跟踪误差动态特性与式(18)类似,这也间接说明了在无扰情况下闭环系统的稳定性是得到保证的.同理,若系统期望跟踪误差动态特性符合式(19),同样可推断出闭环系统误差在无扰情况下是有限时间收敛的.这里不妨作大胆尝试,令系统期望跟踪误差动态特性与式(17)一致,则混合微分器具备的特性,改进后的TLC方法也同样具备,这里需要指出的是,本文针对TLC方法的改进仅利用了混合微分器的非摄动形式,在去噪方面一般采用其摄动形式.
接下来讨论与分析采用式(17)作为LTV期望的误差动态特性时闭环系统的扰动抑制能力,首先给出如下假设和定理:
假设4 存在满足假设1的正的有界实数σ以及正实数M,使下列不等式成立:
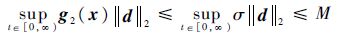
式中:||·||2表示2范数.
定理3 存在满足假设4的正实数M,使得t→∞时,受扰的LTV系统以形如式(18)作为期望误差动态特性时,跟踪误差最终一致有界且绝对值收敛于正紧集合BL:
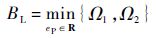
式中:
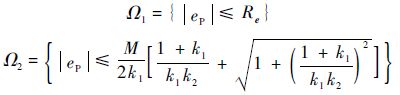
其中:k1=λ2;k2=2/λ均为正数.
证明 受扰的LTV系统以形如式(18)作为期望误差动态特性时,满足状态方程:

构造Laypunov函数:
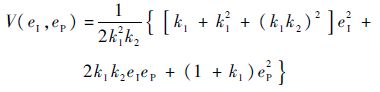
沿闭环系统轨线求函数V(eI,eP)的导数,有
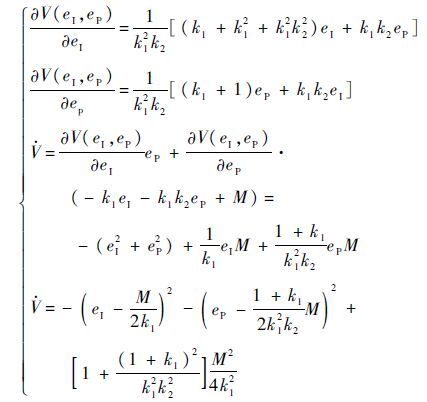
欲使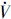 <0成立,须有下式成立:
<0成立,须有下式成立:
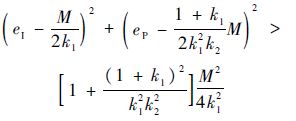
其几何意义在于以|eI|≤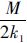 ,|eP|≤
,|eP|≤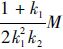 之内的点为圆心,半径为
之内的点为圆心,半径为 的圆内点的并集之外,因此当eI>
的圆内点的并集之外,因此当eI> ,|eP|>
,|eP|>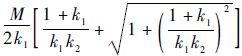 时恒有
时恒有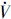 <0,因此如下不等式成立:
<0,因此如下不等式成立:
|eI|≤ 证毕
证毕
由k1=λ2,k2=2/λ可推出|eP|≤(1+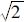 ).M/2k1,不难发现受扰的LTV系统以形如式(18)作为期望误差动态特性时,跟踪误差最终的收敛域与反馈系数k1成反比.
).M/2k1,不难发现受扰的LTV系统以形如式(18)作为期望误差动态特性时,跟踪误差最终的收敛域与反馈系数k1成反比.
同样,下面讨论与分析采用式(19)作为LTV跟踪误差动态特性时系统抑制扰动的能力.
定理4 存在满足假设4的正实数M,使得t→∞时,受扰的LTV系统以形如式(19)作为期望误差动态特性时,跟踪误差最终一致有界且绝对值收敛于正紧集合BR:
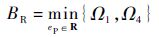
式中:
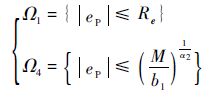
证明 受扰的LTV系统以形如式(19)作为期望误差动态特性时,满足状态方程:

式中:0 <α1<1;0<α2<1.
首先构造如下的Laypunov函数:
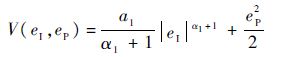
两边对时间求导可得
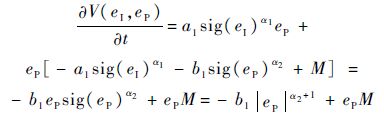
欲使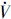 <0成立,须使得
<0成立,须使得
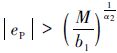
因此闭环系统的跟踪误差将限制在由不等式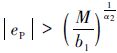 限定的范围之内.证毕
限定的范围之内.证毕
一般而言,反馈增益b1要大于扰动的上界M,故受扰的LTV系统以形如式(19)作为期望误差动态特性时,跟踪误差最终的收敛域比定理3所述的范围小的多.
至此,可以得到如下结论:受扰的LTV系统以形如式(17)作为期望误差动态特性时,实际上也可分为两个阶段:闭环跟踪误差远离原点时,线性反馈占主导成分;反之,闭环跟踪误差逐渐接近原点时,非线性非光滑反馈占主导成分,与混合微分器性质类似,跟踪误差全程均能自动以较快的速度收敛.
现对定理2所述的LTV控制律进行修正可得
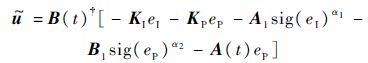
式中:A1和B1为适维的正定对角矩阵,其对角线上相应的元素分别为推论1及定理4中的a1和b1,整个系统经综合后控制律为u=u+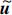 .
.
高超声速飞行器的姿态运动学和动力学方程描述为
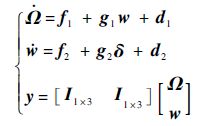
式中:Ω=[α β μ]T为姿态角向量;w=[p r q]T为姿态角速度向量;δ=[δa δr δe]T为副翼、方向舵以及升降舵的舵偏角;f1、g1、f2、g2的详细表达式参考文献[18];d1、d2∈R3×1表示建模误差和外界干扰.显然该系统相对阶为1,并且不存在零动态问题.为验证改进后TLC方法的有效性,将原先的TLC方法以及文献[7]提出的基于单隐层神经网络的鲁棒自适应TLC方法作为对比对象,这里给出文献[7]与本文方法的控制律.
δc=δ+K2(t)ew-G20(vad2+vr2)
式中:vadi(i=1,2)以及vri(i=1,2)分别为慢快回路神经网络的输出项以及自适应鲁棒控制项,具体参数表达式详见文献[7].
本文方法所对应的慢回路控制律为
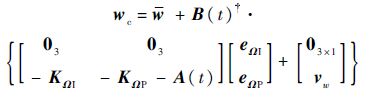
式中:vw=[-a1sig(eΩI)α1-b1sig(eΩP)α2]T;w的解算按照3.1节所述的方法;A(t)和B(t)为慢回路LTV系统中的系统时变矩阵和输入矩阵,可以通过MATLAB符号计算工具箱快速获得.
需要说明的是,由于在慢回路中引入的跟踪微分器已经生成了快回路的标称指令,故快回路采用伪微分器求取角速率的微分信号即可,LTV控制律求法与慢回路类似,这里不再赘述.具体的高超声速飞行器姿态控制系统结构框图如图 1所示.
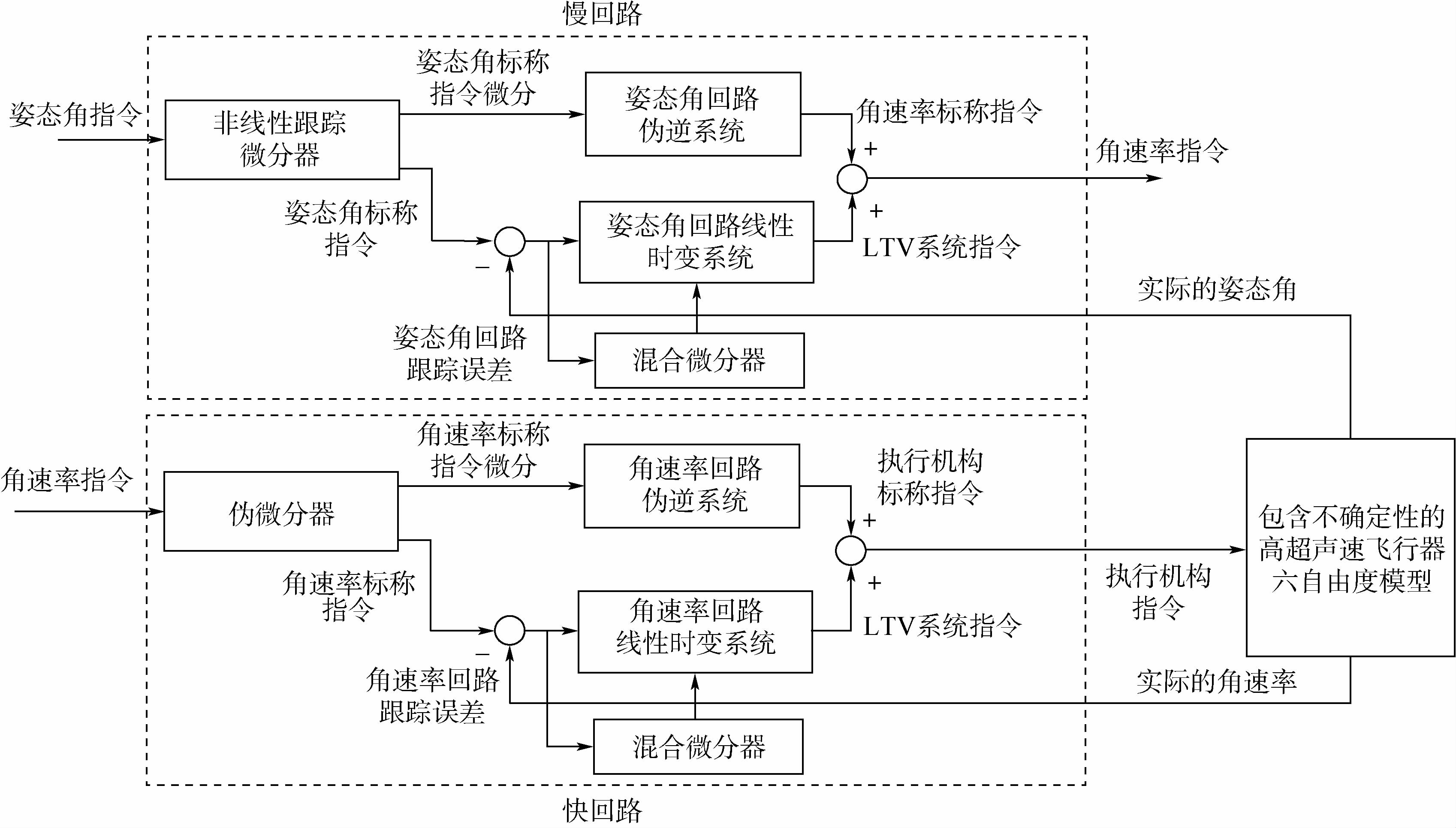
|
| 图 1 高超声速飞行器姿态控制系统结构框图 Fig. 1 Structure diagram of attitude control for hypersonic reentry vehicle |
文献[7]为实现鲁棒自适应控制律需选择合适的设计参数Q(t)、n1、n2、n3、θ、κ、ΓW、ΓV、γφ、λφ,从控制律的参数化描述形式来看,本文设计上更为简洁,且调参数量远少于文献[7];从理论的完备性来看,文献[7]首先要证明神经网络对不确定性的一致逼近能力,其次须设计出合适的权值自适应调节律以及自适应控制律来保证受扰系统所有信号有界.相反,由于本文以混合微分器的非摄动形式作为期望的跟踪误差动态,因此无扰系统的稳定性是直接可以保证的,理论上仅需证明受扰系统跟踪误差的有界性.
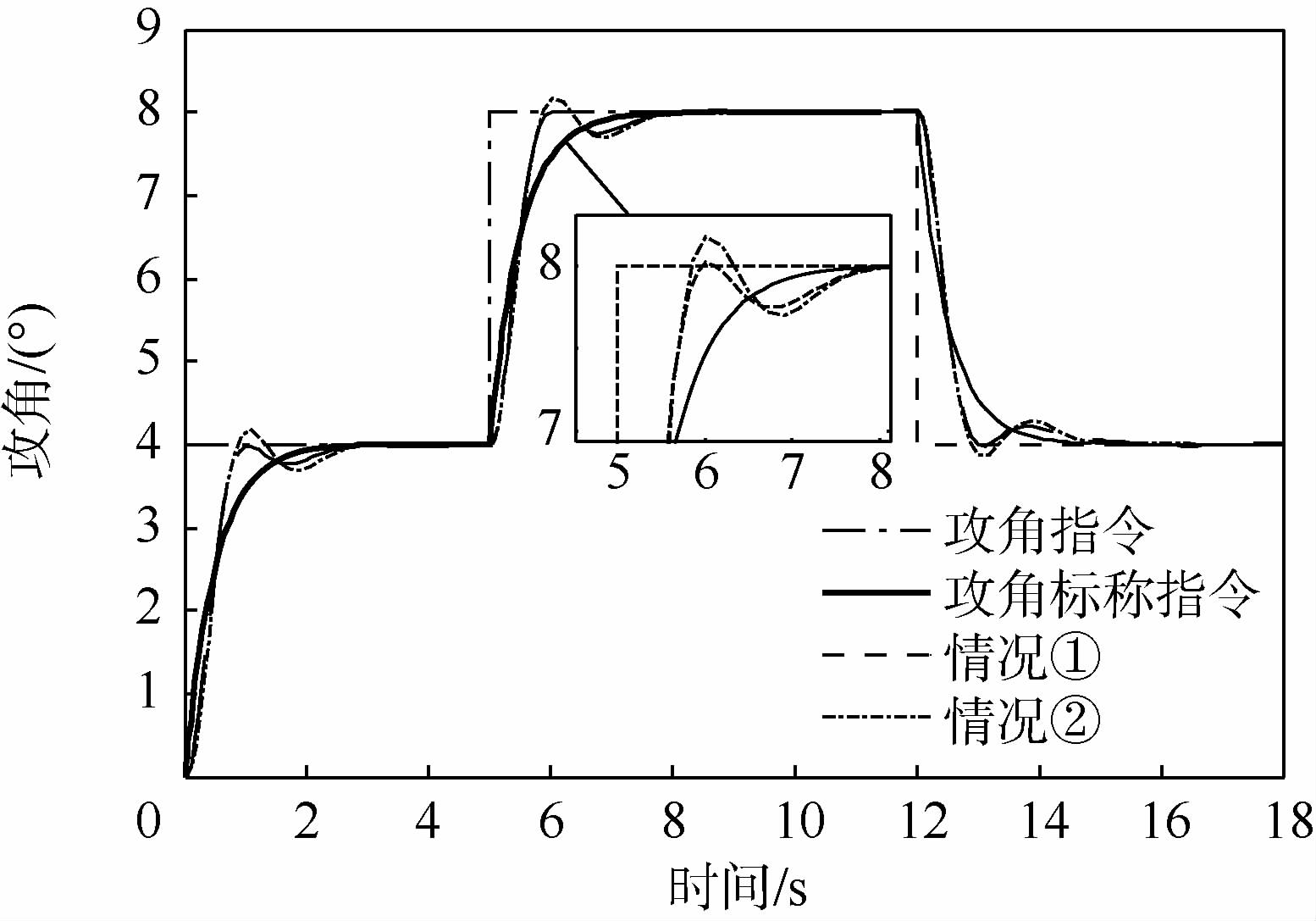
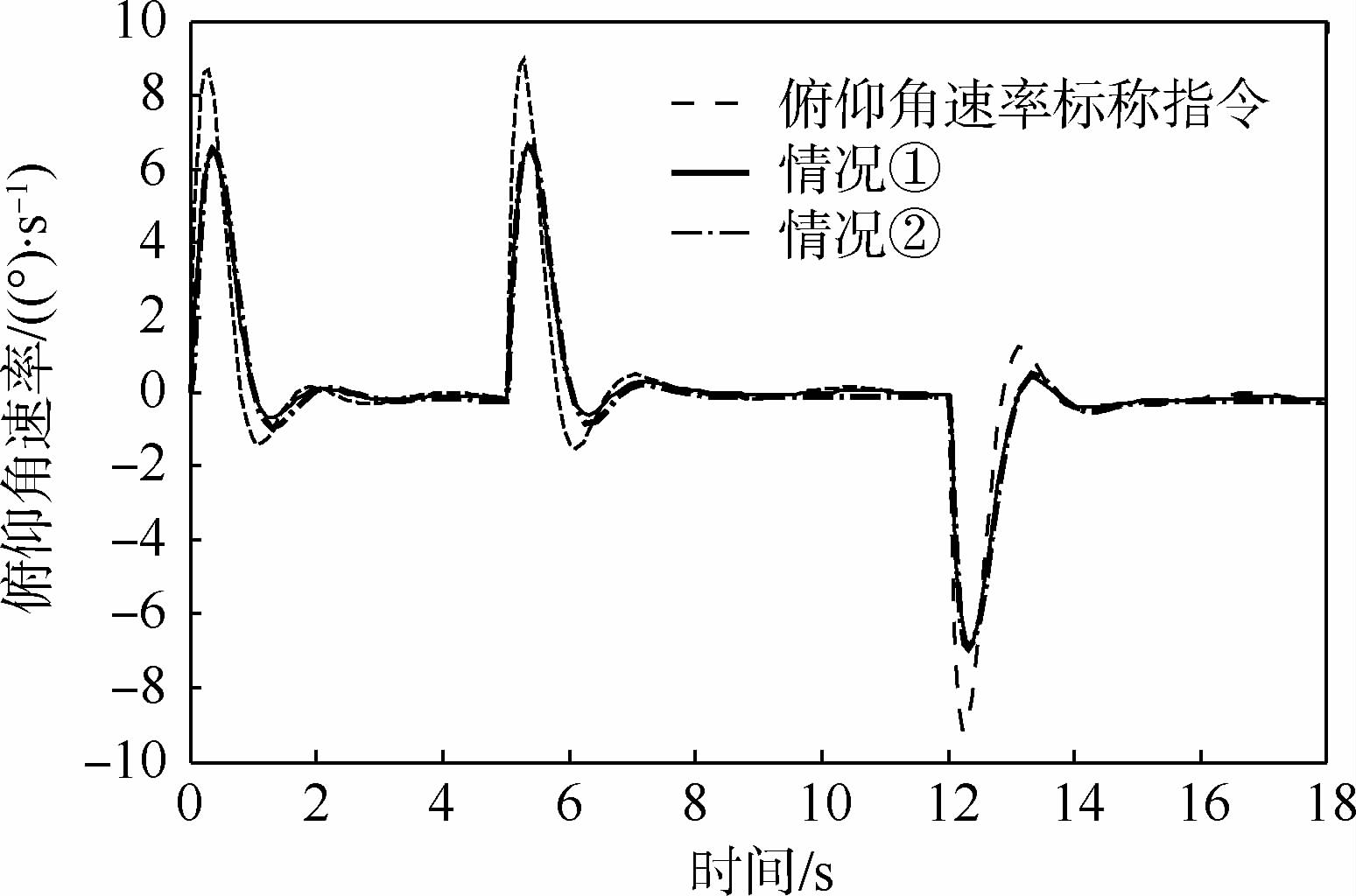
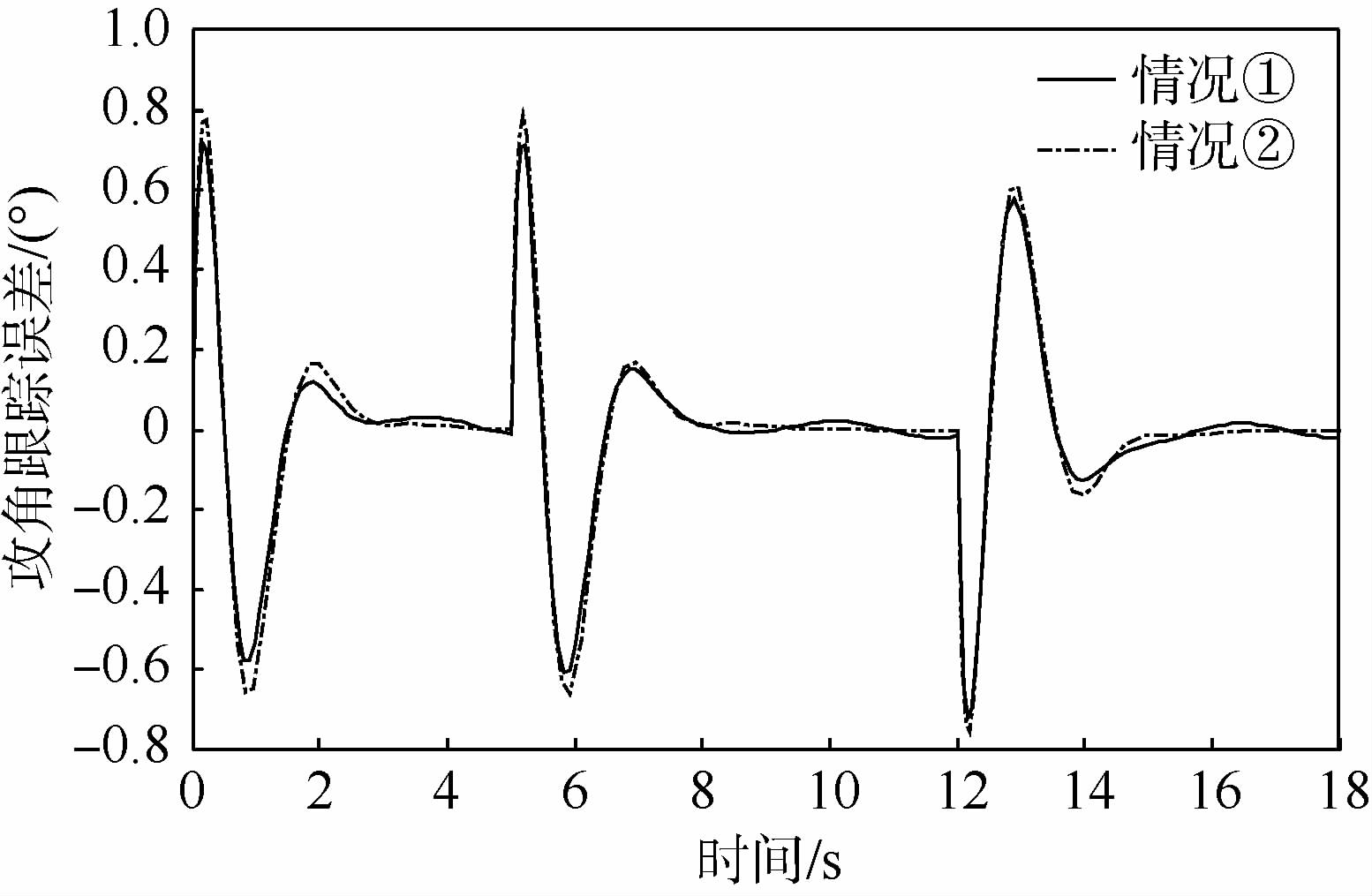
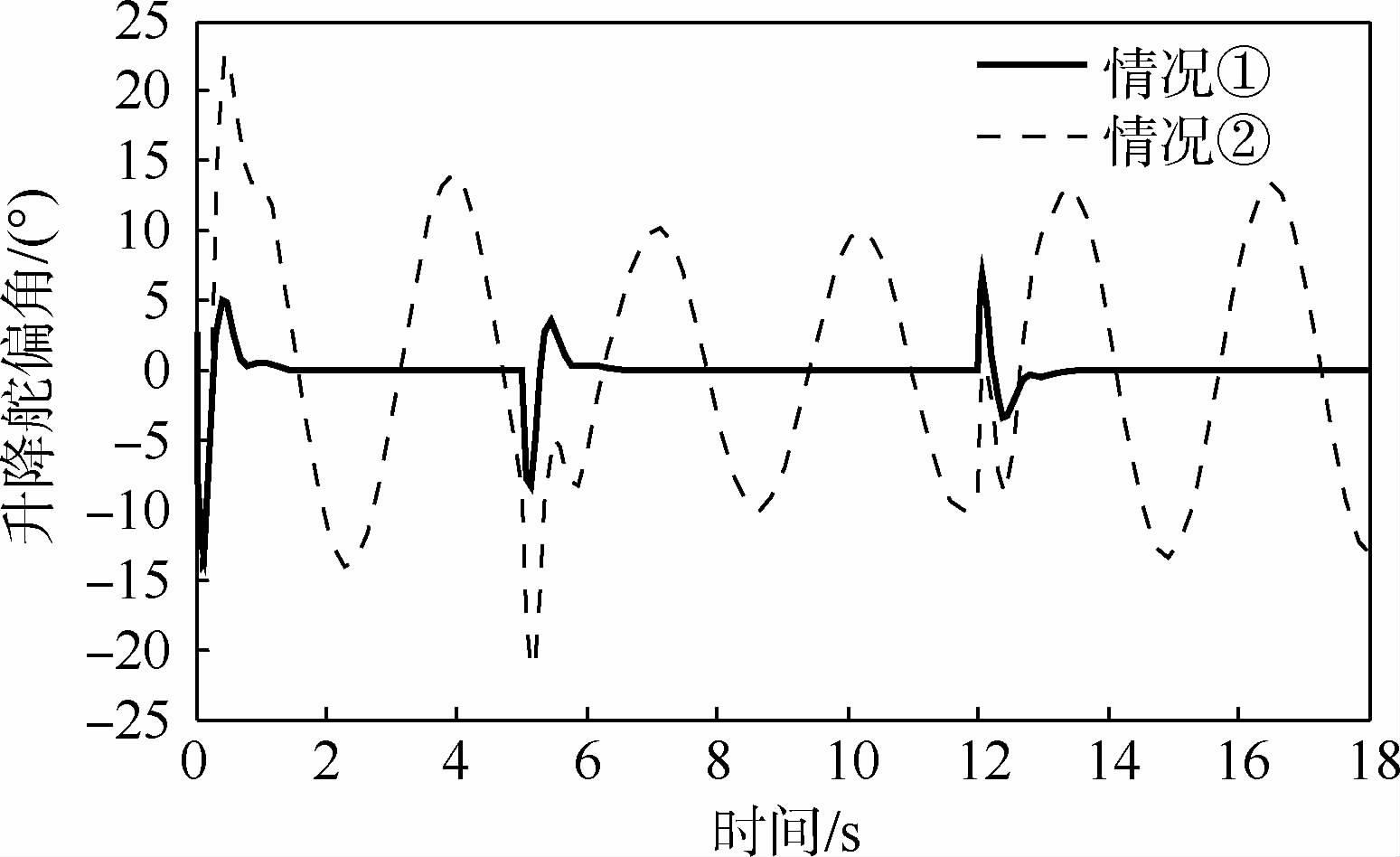
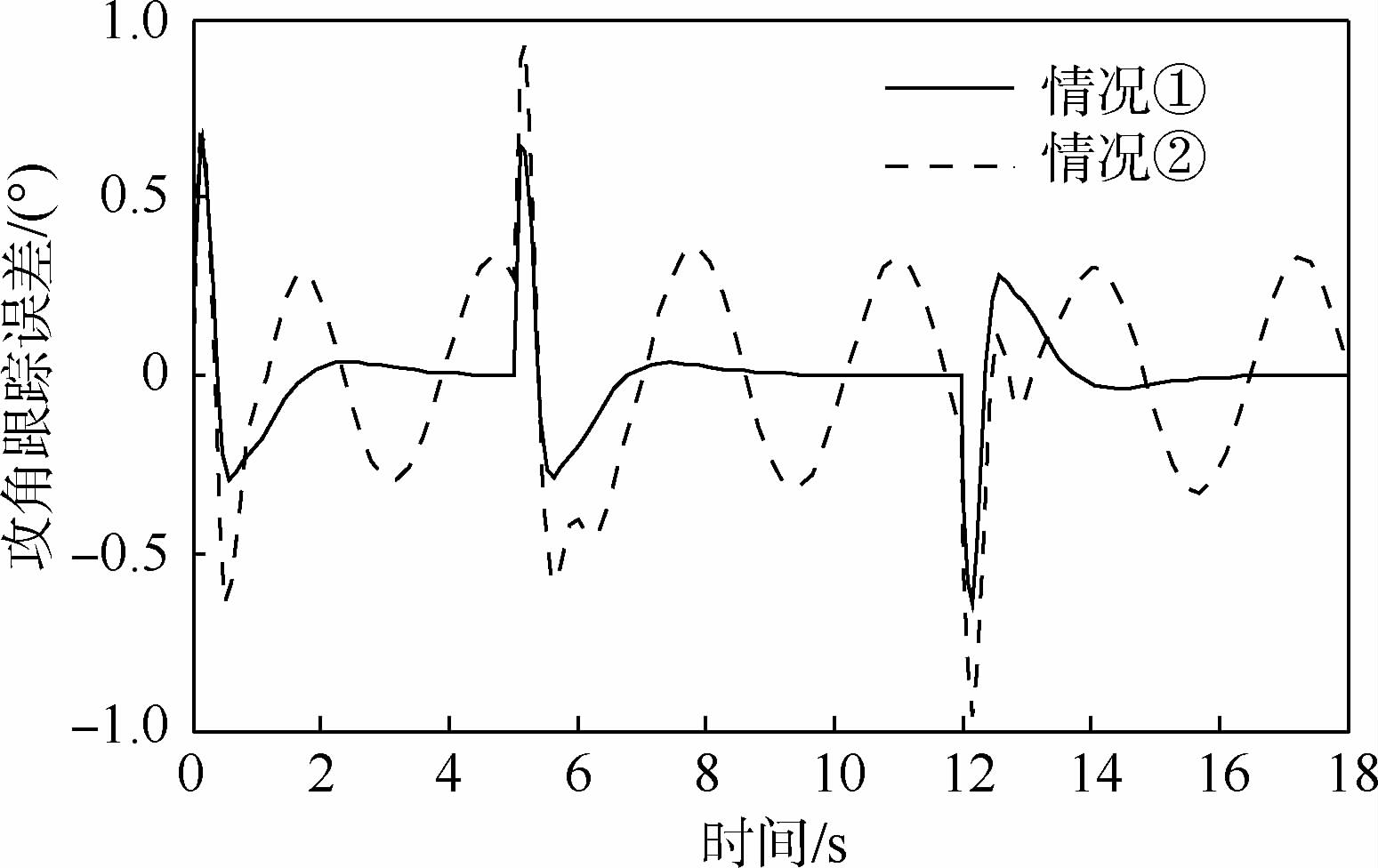
3.2 原先TLC方法的飞行器姿态跟踪控制仿真仿真中高超声速飞行器初始状态选择如下:飞行速度Ma=6.5,飞行高度H=30.9 km,初始姿态角和角速率Ω(0)=w(0)=03×1,系统实现所需的设计参数如下:三通道快、慢回路伪微分器带宽分别为12 rad/s和3 rad/s,LTV系统阻尼参数均为1,相应地快、慢LTV系统的时变带宽为12 rad/s和4 rad/s.考虑到控制品质,标称指令由输入指令经过一阶惯性环节获得,时间常数为0.5 s,三通道舵偏角限幅值均为25°,舵回路均简化为一阶惯性环节,时间常数为0.02 s,以俯仰通道为例,仿真中考虑以下2种情况:①将气动参数不确定设定为-30%;②将气动参数不确定设定为-50%,同时在俯仰通道引入等效干扰力Mzd(t)=975 sin(2t)(单位为N·m),图 2~图 5给出了原先TLC方法的攻角响应曲线、俯仰角速率响应曲线、升降舵偏角响应曲线及攻角跟踪误差曲线.
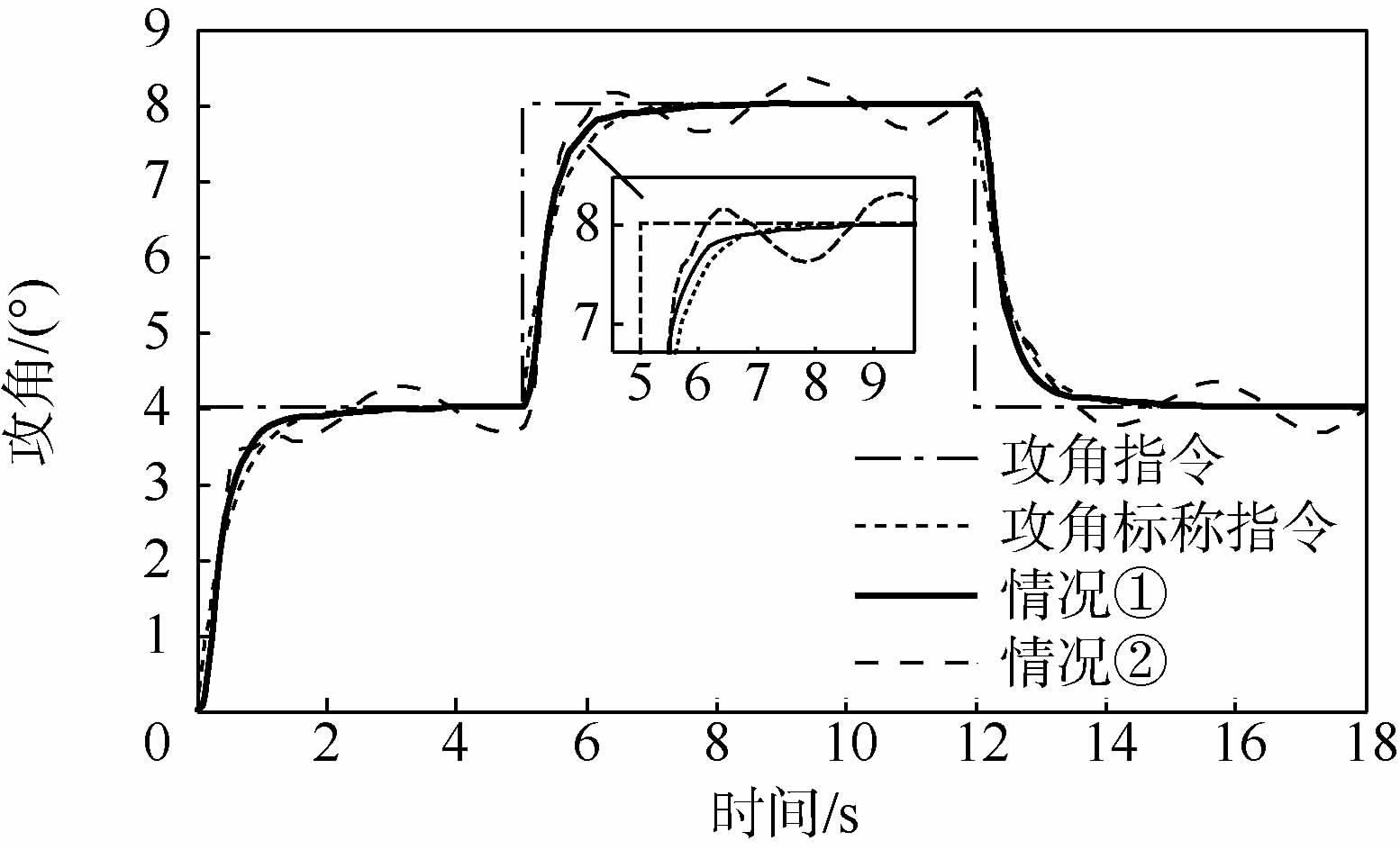
|
| 图 2 原先TLC方法的攻角响应曲线 Fig. 2 Angle of attack response curves for conventional TLC method |
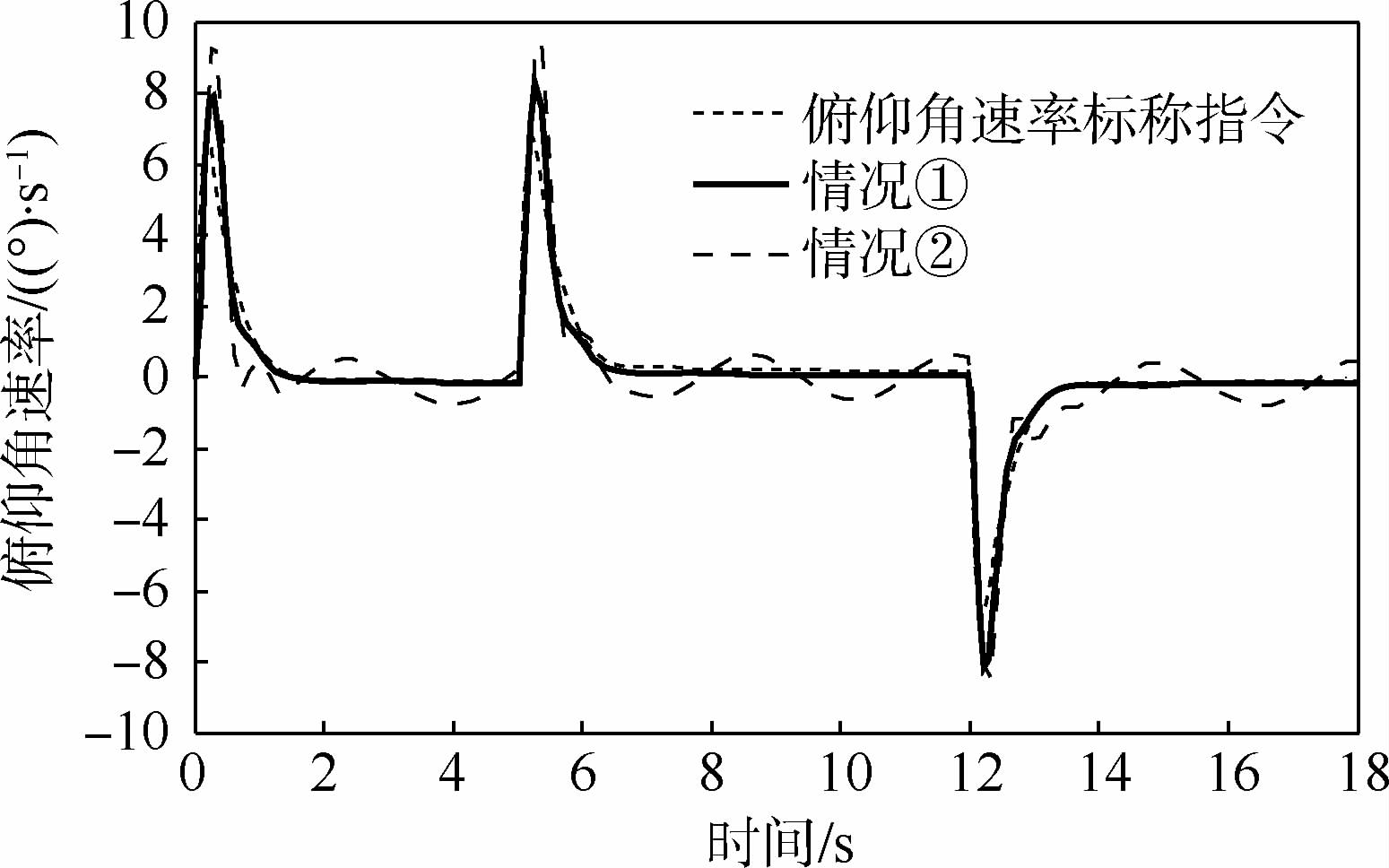
|
| 图 3 原先TLC方法的俯仰角速率响应曲线 Fig. 3 Pitch rate response curves for conventional TLC method |
|
| 图 4 原先TLC方法的升降舵偏角响应曲线 Fig. 4 Deflection angle response curves for conventional TLC method |
|
| 图 5 原先TLC方法的攻角跟踪误差曲线 Fig. 5 Angle of attach tracking error curves for conventional TLC method |
由图 2可以明显看出,当气动参数摄动为-30%时,TLC方法依然体现出较好的控制性能,攻角全程跟踪误差维持在0.8°以内,调节时间约为2 s,且跟踪无超调,过渡过程较平滑.由图 3和图 4可以发现,角速率和舵偏角在过渡阶段会存在剧烈的跳变,验证了2.1节阐述的线性积分链式微分器所产生的峰值效应.可以预见的是,当攻角指令增大时,执行机构在初始阶段更容易饱和.此外,当不确定性增大时,TLC方法难以克服不确定性的影响,导致控制性能恶化,攻角及角速率响应在稳态均呈现震荡行为,如图 2和图 3所示.
3.3 文献[7]方法的飞行器姿态跟踪控制仿真仿真中飞行器的初始状态以及TLC的设计参数与3.2节保持一致,同样以俯仰通道为例,仿真中考虑以下2种情况:①将气动参数不确定设定为-50%,同时在俯仰通道引入等效干扰力Mzd(t)=975 sin(2t)(单位为N·m);②将气动参数不确定设定为-70%,图 6~图 9为文献[7]方法的攻角响应曲线、俯仰角速率响应曲线、升降舵偏角响应曲线及攻角跟踪误差曲线.
可见,在单隐层神经网络的鲁棒自适应控制律的作用下,系统在仿真条件1和仿真条件2下均具有良好的控制性能.由图 6可以看出,攻角响应在过渡阶段具有一定的超调,全程跟踪误差小于0.8°,但当不确定性增加至-70%时,升降舵偏角在过渡阶段迅速跳变至饱和值.可以预见的是,在更恶劣的条件下,文献[7]方法的控制量在过渡阶段会更易超出约束范围.
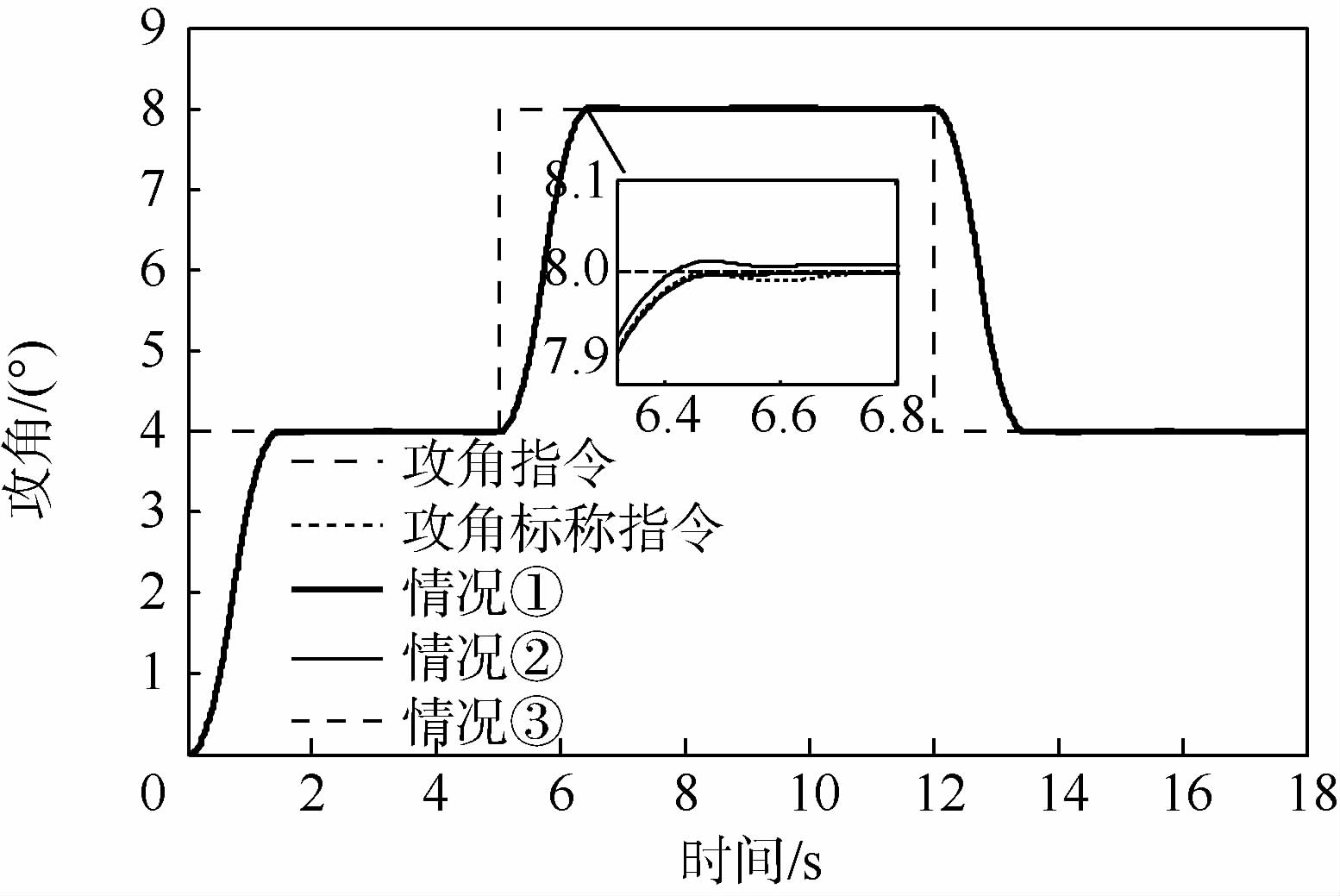
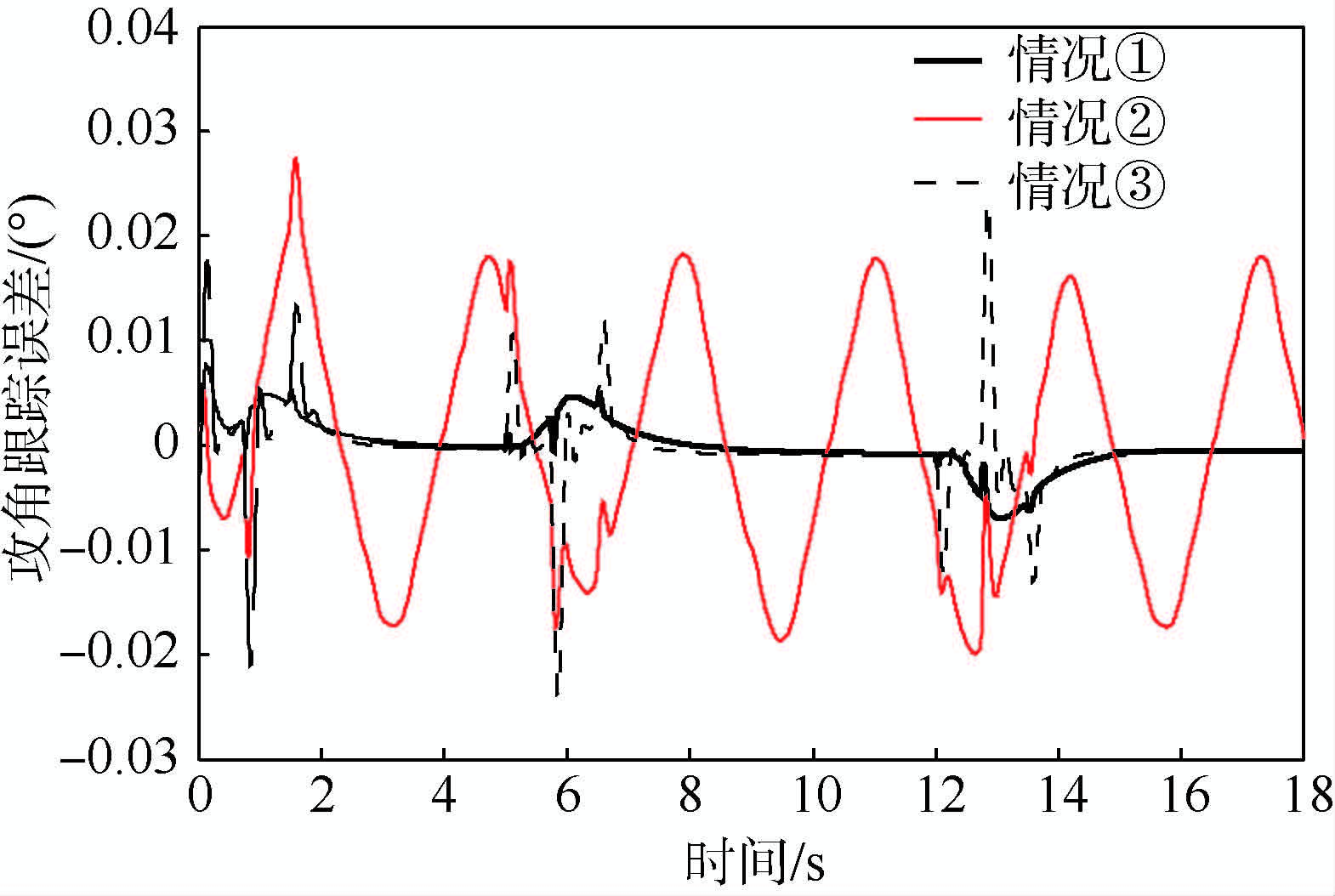
3.4 改进后TLC方法的飞行器姿态跟踪控制仿真仿真中飞行器的初始状态与3.3节保持一致,改进后的TLC控制器参数选择为:非线性跟踪-微分器中积分步长h=0.005 s,加速度饱和值的绝对值|r|=7.449(°)/s2,LTV慢回路控制器的参数为KΩI=42I3×3,KΩP=2×4I3×3,相应地LTV快回路控制器的参数为KWI=122I3×3,KWP=2×12I3×3,此时能够满足奇异摄动的时标分离理论,LTV慢回路中混合微分器的参数取为a1=b1=2,α1=α2=0.8,LTV快回路中混合微分器的参数取为a1=b1=4,α1=α2=0.8,仿真中考虑以下3种情况:①将气动参数不确定设定为-30%;②将气动参数不确定设定为-50%,同时在俯仰通道引入等效干扰力矩Mzd(t)=975 sin(2t)(单位为N·m);③将气动参数不确定性设定为-80%,考察改进后TLC方法在恶劣条件下的控制性能以及抗干扰能力.同样以俯仰通道为例,图 10~图 13给出了改进后TLC方法的攻角响应曲线、俯仰角速率响应曲线、升降舵偏角响应曲线及攻角跟踪误差曲线.
|
| 图 10 改进后TLC方法的攻角响应曲线 Fig. 10 Angle of attack response curves for proposed TLC method |

|
| 图 11 改进后TLC方法的俯仰角速率响应曲线 Fig. 11 Pitch rate response curves for proposed TLC method |

|
| 图 12 改进后TLC方法的升降舵偏角响应曲线 Fig. 12 Deflection angle response curves for proposed TLC method |
|
| 图 13 改进后TLC方法的攻角跟踪误差曲线 Fig. 13 Angle of attack tracking error curves for proposed TLC method |
由图 13可以发现,情况①下攻角全程跟踪误差小于0.01°,当不确定性足够大时,攻角全程跟踪误差维持在0.03°以内,且攻角输出均可以快速无超调地跟踪上标称指令,过渡过程较平滑,调节时间为1.46 s(符合定理1所述的过渡过程时间的计算公式),与改进前相比,响应的快速性以及鲁棒性均有所提升.此外,由图 11可以看出,通过韩式跟踪微分器求取的角速率标称指令不存在改进前TLC方法中的过渡阶段的快速跳变现象,同时根据定理1可知,减小加速度饱和值可以降低角速率的峰值以及图 11中对称三角形的斜率,故可综合根据系统所能提供的控制量和响应快慢折中选取加速度饱和值.在上述3种仿真条件下,本文方法的控制性能都明显优于文献[7],并且在控制量的约束范围内可容忍更大的不确定性(达到-80%).
4 结 论本文针对当前轨迹线性化控制(TLC)方法对系统中的不确定性存在鲁棒性不足的问题,受非线性跟踪微分器设计思路的启发,并立足于TLC方法的理论框架提出了一种可最大程度保留其优良特性的改进方案.
1) 采用韩式跟踪微分器替换原先的一阶惯性+伪微分器环节,有效抑制了峰值现象.
2) 通过构造期望的跟踪误差动态直接获取线性时变系统(LTV)的控制量,并将混合微分器的非摄动形式等价为期望的跟踪误差动态,以提升TLC的鲁棒性,该处理方式使得控制器设计更为简洁、易于工程实现.
3) 即使气动参数不确定性增加至-80%,改进后的TLC依然具有良好的控制性能,全程跟踪误差维持在0.03°以内,能够满足高超声速飞行器快时变、高精度以及强鲁棒的控制需求.
| [1] | Zhu J J, Banker B D, Hall C E.X-33 ascent flight control design by trajectory linearization-a singular perturbation approach[C]// AIAA Guidance, Navigation and Control Conference.Reston: AIAA, 2000: 4159-4178. |
| Click to display the text | |
| [2] | Bevacqua T, Best E, Huizenga A, et al.Improved trajectory linearization flight controller for reusable launch vehicles[C]//AIAA Aerospace Sciences Meting and Exhibit.Reston: AIAA, 2004: 875-887. |
| Click to display the text | |
| [3] | Liu Y, Zhu J J, Robert L, et al.Omni-directional mobile robot controller based trajectory linearization[J].Robotics and Autonomous Systems, 2008, 56(5): 461-479. |
| Click to display the text | |
| [4] | Liu Y, Zhu J J. Regular perturbation analysis for trajectory linearization control[C]//Proceedings of the 2007 American Control Conference.Piscataway, NJ: IEEE Press, 2007: 3053-3058. |
| Click to display the text | |
| [5] | Liu Y, Huang R, Zhu J J.Adaptive neural network control based on trajectory linearization control[C]//The 6th World Congress on Intelligent Control and Automation.2006: 417-421. |
| Click to display the text | |
| [6] | 朱亮, 姜长生, 陈海通, 等.基于单隐层神经网络的空天飞行器直接自适应轨迹线性化控制[J].宇航学报, 2006, 27(3): 338-344. Zhu L, Jiang C S, Chen H T, et al.Direct adaptive trajectory linearization control of aerospace vehicle using SHLNN[J].Journal of Astronautics, 2006, 27(3): 338-344(in Chinese). |
| Cited By in Cnki (32) | |
| [7] | 朱亮, 姜长生, 薛雅莉.基于单隐层神经网络的空天飞行器鲁棒自适应轨迹线性化控制[J].兵工学报, 2008, 29(1): 52-56. Zhu L, Jiang C S, Xue Y L.Robust adaptive trajectory linearization control for aerospace vehicle using single hidden layer neutral networks[J].Acta Armamentarii, 2008, 29(1): 52-56(in Chinese). |
| Cited By in Cnki (8) | |
| [8] | 薛雅丽, 姜长生, 朱亮. 一类径向基神经网络干扰观测器轨迹线性化控制[J].系统工程与电子技术, 2008, 19(4): 522-526. Xue Y L, Jiang C S, Zhu L.Trajectory linearization control of an aerospace vehicle based on RBF neutral network[J].Journal of Systems Engineering and Electronics, 2008, 19(4): 522-526(in Chinese). |
| [9] | Jiang C S, Zhang C Y, Zhu L.Research of robust adaptive trajectory linearization control based on T-S fuzzy system[J].Journal of Systems Engineering and Electronics, 2008, 19(3): 537-545. |
| Click to display the text | |
| [10] | 韩京清, 袁露林. 跟踪-微分器的离散形式[J].系统科学与数学, 1999, 19(3): 268-273. Han J Q, Yuan L L.The discrete tracking differentiator[J].System Science and Mathematics, 1999, 19(3): 268-273(in Chinese). |
| Click to display the text | |
| [11] | Su Y X, Duan B Y, Zheng C H, et al.Disturbance-rejection high-precision motion control of a stewart platform[J].IEEE Transactions on Control Systems Technology, 2004, 12(3): 264-274. |
| Click to display the text | |
| [12] | 王新华, 陈增强, 袁著祉.全程快速非线性跟踪-微分器[J].控制理论与应用, 2003, 20(6): 875-878. Wang X H, Chen Z Q, Yuan Z Z.Nonlinear tracking-differentiator with high speed in whole course[J].Journal of Control Theory & Applications, 2003, 20(6): 875-878(in Chinese). |
| Click to display the text | |
| [13] | Wang X H, Chen Z Q.Finite-time-convergent differentiator based on singular perturbation technique[J].IEEE Transactions on Automatic Control, 2007, 52(9): 1731-1737. |
| Click to display the text | |
| [14] | 宿敬亚, 张瑞峰, 王新华, 等.基于滤噪微分器的四旋翼飞行器控制[J].控制理论与应用, 2009, 26(8): 827-832. Su J Y, Zhang R F, Wang X H, et al.Controlling a four-rotor aircraft based on noise-attenuation differentiator[J].Journal of Control Theory & Applications, 2009, 26(8): 827-832(in Chinese). |
| Cited By in Cnki (15) | |
| [15] | Ibrir S. Linear time-derivative trackers[J].Automatica, 2004, 40(3): 397-405. |
| Click to display the text | |
| [16] | 韩京清. 自抗扰控制技术[M].北京: 国防工业出版社, 2008: 56-66. Han J Q.Active disturbance rejection control technique[M].Beijing: National Defense Industry Press, 2008: 56-66(in Chinese). |
| [17] | Haimo V T. Finite time controllers[J]Siam Journal on Control and Optimization, 1986, 24(4): 760-771. |
| Click to display the text | |
| [18] | 陈小庆. 高超声速滑翔飞行器机动技术研究[D].长沙: 国防科学技术大学, 2011. Chen X Q.The key technology relative to the maneuverability of hypersonic gliding vehicle[D].Changsha: National University of Defense Technology, 2011(in Chinese). |
| Click to display the text |