实际工程中的地基土在交通、地震、波浪等往返荷载作用下应力状态变化复杂,通常不仅主应力幅值会随时间往复变化,主应力的方向亦会循环旋转[1].目前应力主轴旋转对土体变形特性的影响已引起国内外学者的广泛关注,采用方向剪切盒、空心圆柱扭剪仪等试验设备开展了较为系列的试验研究[2, 3, 4, 5, 6, 7, 8, 9, 10, 11].应力主轴旋转条件下砂土的主要试验规律可总结如下:①纯应力主轴循环旋转可产生与应力主轴固定单调剪切处于同一数量级的塑性变形.②应力主轴旋转导致砂土产生体缩趋势,在不排水条件表现为正超静孔隙水压力的不断累积,可导致液化等破坏发生.③应力主轴旋转条件下塑性应变增量主轴与应力主轴之间存在显著的非共轴现象.④中主应力对应力主轴循环旋转条件下砂土的变形特性有重要影响,体缩应变(不排水条件下为正超静孔隙水压力)趋势随中主应力系数的增加而增加.
土体宏观上表现出的力学特性与细观组构及演化规律密切相关.离散元法具有可保证初始试样完全相同以及可获得任意加载时刻颗粒的空间分布和接触特征等优点,已成为分析岩土材料细观变形机理的有效工具.值得指出的是,至今为止的离散元数值模拟主要基于颗粒材料双轴压缩、三轴压缩、直剪试验、单剪试验等单调加载的模拟.Li和Yu[12]在应力主轴旋转条件下颗粒材料的离散元数值模拟取得了突破性进展.他们采用六边形的试样,有效实现了纯应力主轴旋转的加载,并较为深入地分析了颗粒材料非共轴的细观物理机制.但在他们的研究中,试样的颗粒形状均为圆形,无法反映试样沉积过程中颗粒形状产生的初始各向异性的影响.为了合理反映颗粒形状及试样初始各向异性的影响,本文的离散元数值模拟采用椭圆形的颗粒材料,且模拟重力作用下颗粒的沉积过程生成试样.在验证应力主轴旋转离散元数值模拟有效性的基础上,对应力主轴旋转条件下颗粒材料的细观组构特征及演化规律进行了分析,以望对应力主轴旋转条件下颗粒材料的细观物理机制研究有所裨益.
1 离散元数值模拟本文离散元数值模拟采用现在美国劳伦斯·利弗莫尔国家实验室从事岩土工程数值分析研究工作的付鹏程博士开发的PPDEM.付鹏程和Dafalias[13, 14]对直剪试验和双轴压缩试验进行了系列的数值模拟,充分证实了该离散元程序在单调加载条件下的有效性.而相比于单调加载,应力主轴旋转加载的实现要复杂很多.为了实现应力主轴旋转,Li和Yu[12]数值模拟中的应力通过伺服控制动态边界条件的方式施加.本文中应力主轴旋转的加载摒弃了伺服控制动态边界条件的方法,而是开发了一种可施加任意边界应力状态的新方法.图 1所示为应力主轴旋转条件下应力边界的施加模式.该方法能自动识别加载过程中处于边界上的颗粒,沿主应力方向作用的力则直接施加在边界颗粒上.这种应力边界条件施加方法具有允许试样自由变形、且可保证所施加应力场的均匀性等优点.
 |
| 图 1 应力主轴旋转边界应力的施加方式说明Fig. 1 Illustration of applied mode of boundary stress under rotation of principal stress axes |
离散元数值模拟采用长短轴比均为3.0的椭圆形颗粒,颗粒长轴变化范围为0.30~1.00 mm.制样过程采用付鹏程和Dafalias[13, 14]相同的方法,即先生成20 000个椭圆颗粒,对椭圆颗粒施加重力模拟实际工程土体的沉积过程,将20 000个椭圆颗粒沉积在一个方形试样盒中.然后用一个圆形覆盖截取出图 1所示的圆形试样,即可进行接下来的固结和应力主轴旋转加载.本文采用的圆形覆盖半径为15 mm,包含6 000个左右的椭圆颗粒.
数值模拟试验施加的应力路径为:先对试样进行不等向固结,然后纯应力主轴循环旋转加载.具体加载过程为:对截取出的圆形试样沿图 1所示的v轴和h轴施加大小主应力σ1和σ3进行不等向固结,此时大主应力σ1与v轴之间形成的大主应力方向角ασ=0°.试样固结完成后即进行纯应力主轴循环旋转加载:保持大小主应力幅值不变,而大主应力方向角ασ在0°~180°之间连续旋转.由于主应力幅值在应力主轴旋转过程中保持不变,因此试样的变形仅由主应力方向变化产生.数值模拟试验方案如表 1所示,所施加的球应力均为200 kPa,对初始孔隙比不同的4个试样进行了多种不同应力比的纯应力主轴循环旋转试验,共计14组.数值模拟采用的主要细观参数为:颗粒之间的摩擦角为30°,颗粒之间的切向刚度为2 100 MPa,切向刚度与法向刚度的比值取0.33.
| 初始孔隙比e0 | 施加的应力比 R=(σ1-σ3)/(σ1+σ3) |
球应力p/kPa |
| 0.275 | 0.05/0.10/0.15/0.20/0.25/0.30 | 200 |
| 0.251 | 0.10/0.15/0.20/0.25/0.30/0.35 | |
| 0.235 | 0.30 | |
| 0.210 | 0.30 |
以试样初始孔隙比e0=0.251,应力比R=0.3的数值模拟试验为例,图 2所示为一个循环周期内实际施加在试样上的应力路径,其中的应力通过计算颗粒之间的接触力而得.分析图 2可知,在一个循环周期内,大小主应力幅值保持不变,大主应力方向角ασ从0°线性增加到180°,与设计的加载路径一致.由此可见,新开发的数值模拟方法能有效地实现应力主轴旋转加载路径.
 |
| 图 2 数值模拟实现的应力路径Fig. 2 Achieved stress path for numerical simulation |
基于开发的数值模拟方法,图 3和图 4分别给出了上述典型数值模拟试验中正应变分量与循环周数的关系曲线以及剪应力-剪应变关系曲线.张建民和童朝霞等[9, 10, 11]采用空心圆柱扭剪仪对饱和砂土进行了较为系列的纯应力主轴循环旋转排水试验,分析了中主应力系数对应力主轴旋转条件下砂土力学特性的影响.当中主应力系数b=0.1时,径向应变较小,近似于平面应变.本文数值模拟是二维的,将图 3与他们论文中b=0.1的试验成果对比发现:数值模拟能较好地反映物理试验中正应变的发展规律.2个正应变分量(εvv和εhh)随循环周数的增加,均呈周期性循环变化.竖向应变分量εvv主要为拉伸应变,随着循环周数的增加,向出现压缩应变的方向发展.产生的水平应变分量εhh为压缩应变,随循环周数的增加,压缩应变不断累积,但累积速率呈递减趋势.如图 4所示,数值模拟试验中同样观察到剪应力-剪应变关系曲线构成的滞回圈.在循环初期,滞回圈为未封闭的,随循环周数的增加,滞回圈趋向于一闭合的椭圆.由于应力主轴循环旋转下砂土不断硬化,双幅剪应变呈递减趋势.
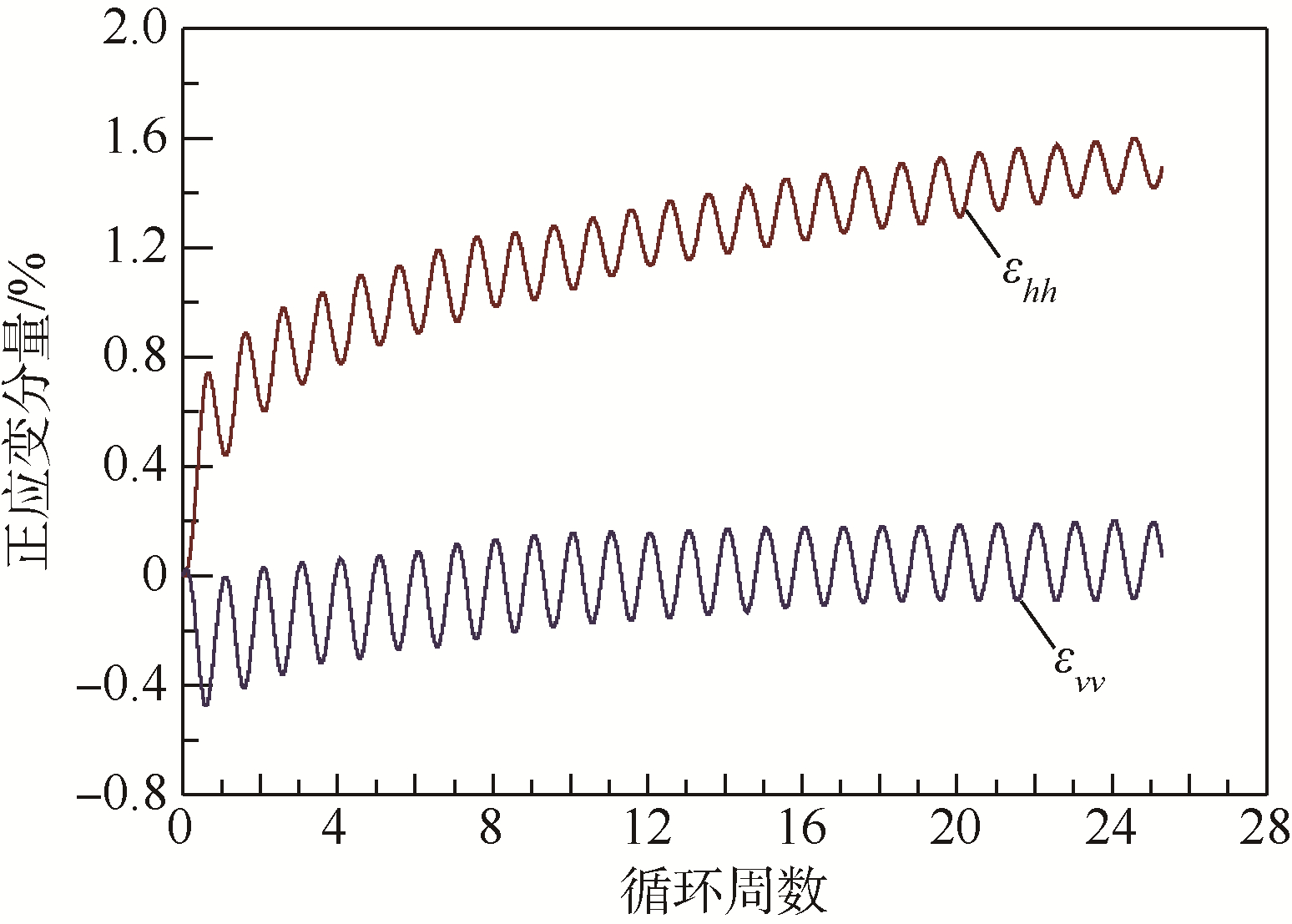 |
| 图 3 正应变分量与循环周数的关系曲线Fig. 3 Relation curve of normal strain components changing with cycle number |
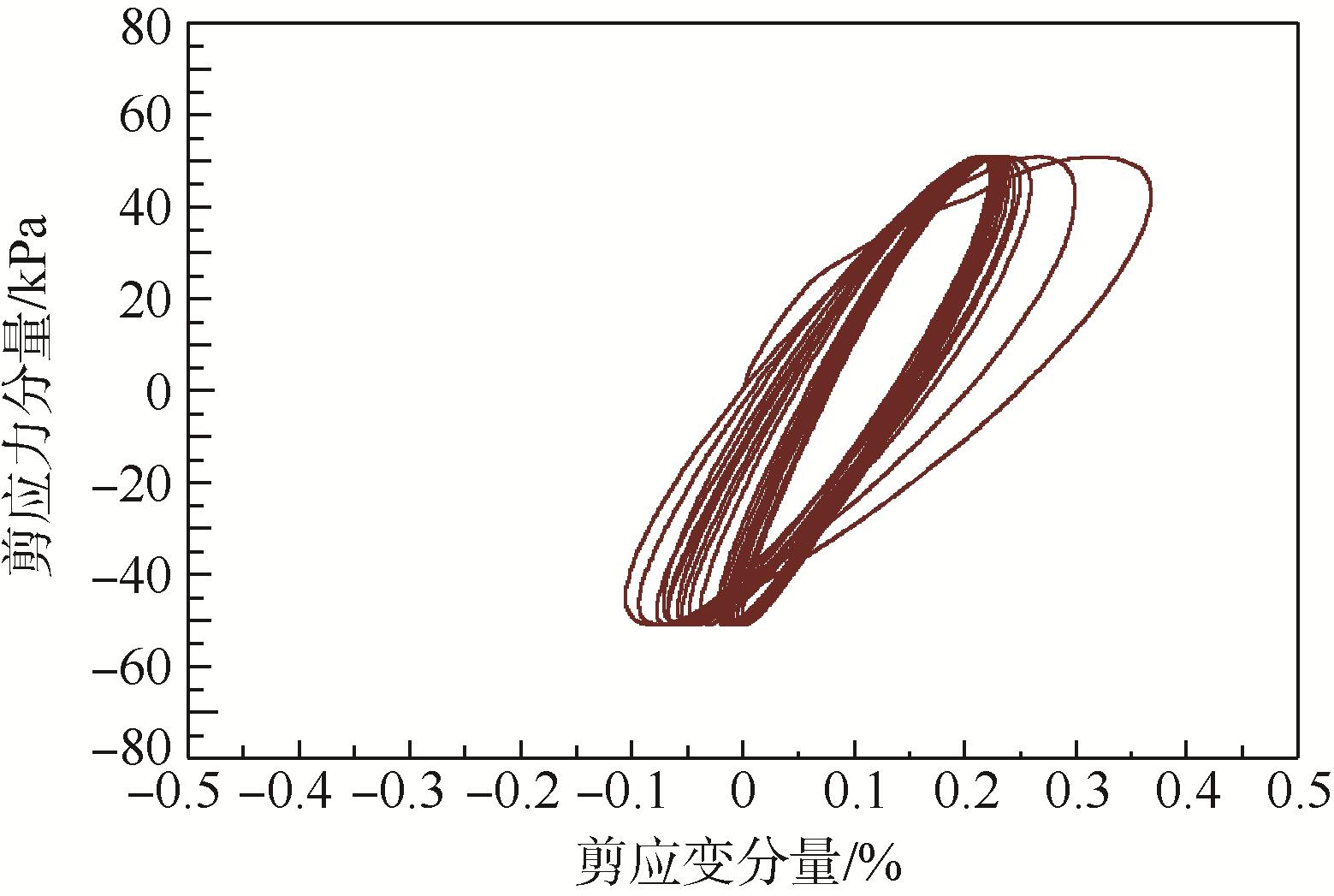 |
| 图 4 剪应力-剪应变关系Fig. 4 Relationship between shear stress and strain |
应力主轴循环旋转下体应变的发展规律如图 5和图 6所示.其中图 5主要反映应力比对体应变发展规律的影响,各试样的初始孔隙比e0=0.251.图 6主要反映初始孔隙比的影响,各试样施加的应力比R=0.3.将图 5和图 6与张建民和童朝霞等[9, 10, 11]的物理试验结果对比可知,数值模拟能较好地反映物理试验中观察到的体应变发展规律.譬如,应力主轴旋转下颗粒材料表现为体缩趋势,体缩应变随应力主轴循环旋转呈周期性波动变化;随循环周数增加体缩应变不断累积,但累积速率呈递减趋势;同时,应力比越大、初始孔隙比越小,体应变的累积速率越大.
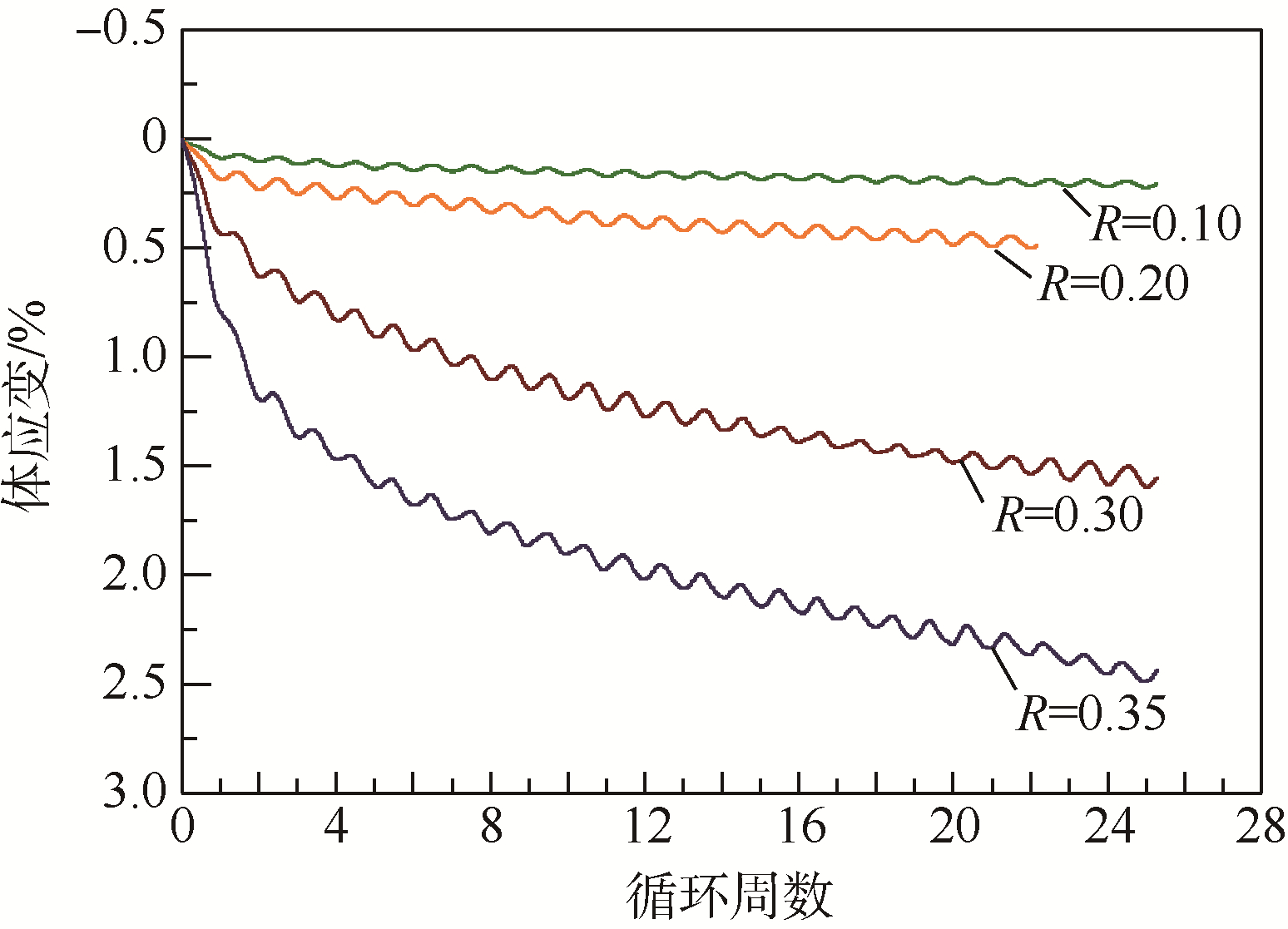 |
| 图 5 应力比对体应变发展的影响(e0=0.251)Fig. 5 Effects of stress ratio on development of volumetric strain (e0=0.251) |
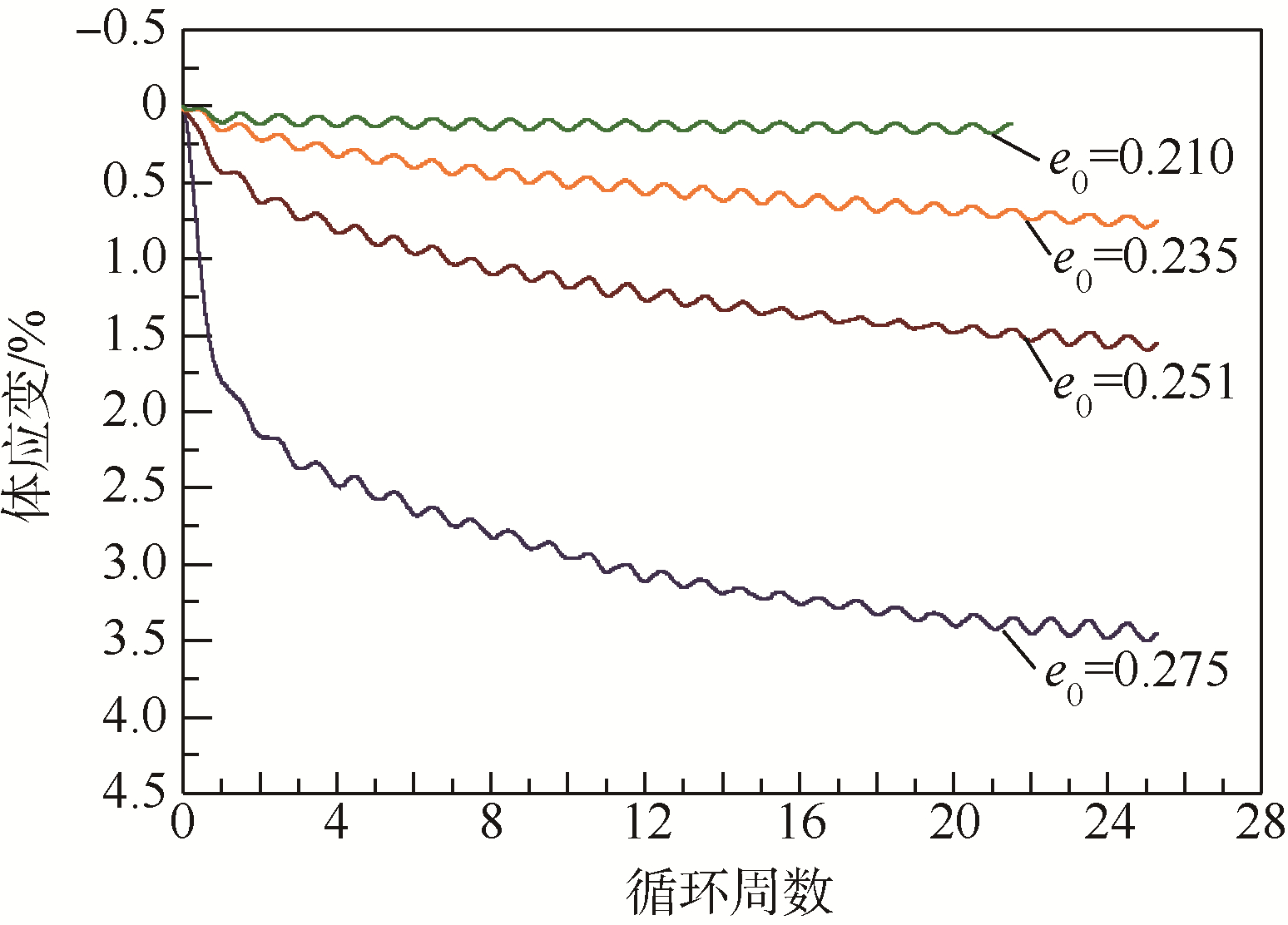 |
| 图 6 初始孔隙比对体应变发展的影响(R=0.3)Fig. 6 Effects of initial void ratio on development of volumetric strain (R=0.3) |
应力主轴旋转下颗粒材料的宏观变形特性与细观组构及其演化规律密切相关.颗粒材料长轴定向及粒间接触法线的空间分布常用组构张量进行表述.在参考已有研究[14, 15]基础上,本文采用式(1)、式(2)分别计算颗粒长轴定向组构张量(Fp)和粒间接触法线组构张量(Fc):
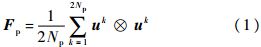
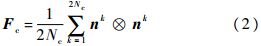
式中:Np和Nc分别为颗粒数量以及颗粒接触数量;uk为第k个颗粒长轴定向的单位向量;nk为第k个粒间接触的单位法向向量; 为2个矢量的张量积.
为2个矢量的张量积.
颗粒长轴定向组构张量(Fp)和粒间接触法线组构张量(Fc)是对称的,它们的积等于1.本文采用以下4个量定量描述颗粒材料的组构特征:
αp:颗粒长轴定向组构张量(Fp)两主值的差,用于反映颗粒定向分布的各向异性程度.该值变化范围在0~1之间,αp=0表示颗粒长轴定向为各向同性,αp越大则颗粒长轴定向各向异性程度越强.
θp:颗粒长轴定向组构张量(Fp)的主方向,可认为是所有颗粒的平均定向角.
αc:粒间接触法线组构张量(Fc)两主值的差,用于反映颗粒接触分布的各向异性程度.与αp类似.
θc:粒间接触法线组构张量(Fc)的主方向,可认为是所有颗粒间接触法线的平均定向角.
仍以试样初始孔隙比e0=0.251及应力比R=0.3的数值模拟试验为例,图 7所示为循环周数N=1,12和22时颗粒组构4个特征变量(αp、θp、αc和θc)在一个完整循环周内的演化规律.
分析图 7可知,反映颗粒长轴定向各向异性程度的变量αp在大主应力方向角ασ从0°旋转到180°的单个循环周内基本没有发生变化,循环周数对αp亦无明显影响.颗粒长轴定向角θp在单个循环周内呈正弦式周期性变化,随循环周数增加θp的变化幅值呈递减趋势,但总体θp的变化幅度非常小.这表明颗粒长轴定向组构特征在应力主轴旋转过程中变化非常小.相比于颗粒长轴定向组构,粒间接触法线组构在应力主轴旋转过程中变化较明显.反映粒间接触法线分布各向异性程度的变量αc在单个循环周内呈余弦式变化,约在ασ=90°时达到最小值,而在ασ=0°和180°时达到最大值.αc的变化幅度随旋转周数增加有增大的趋势.粒间接触法线角度θc在竖轴(v轴)附近摆动,在一个循环周内呈正弦式变化规律.随循环周数增加,θc的变化幅度呈递减趋势,但远小于应力主轴旋转幅度(180°).
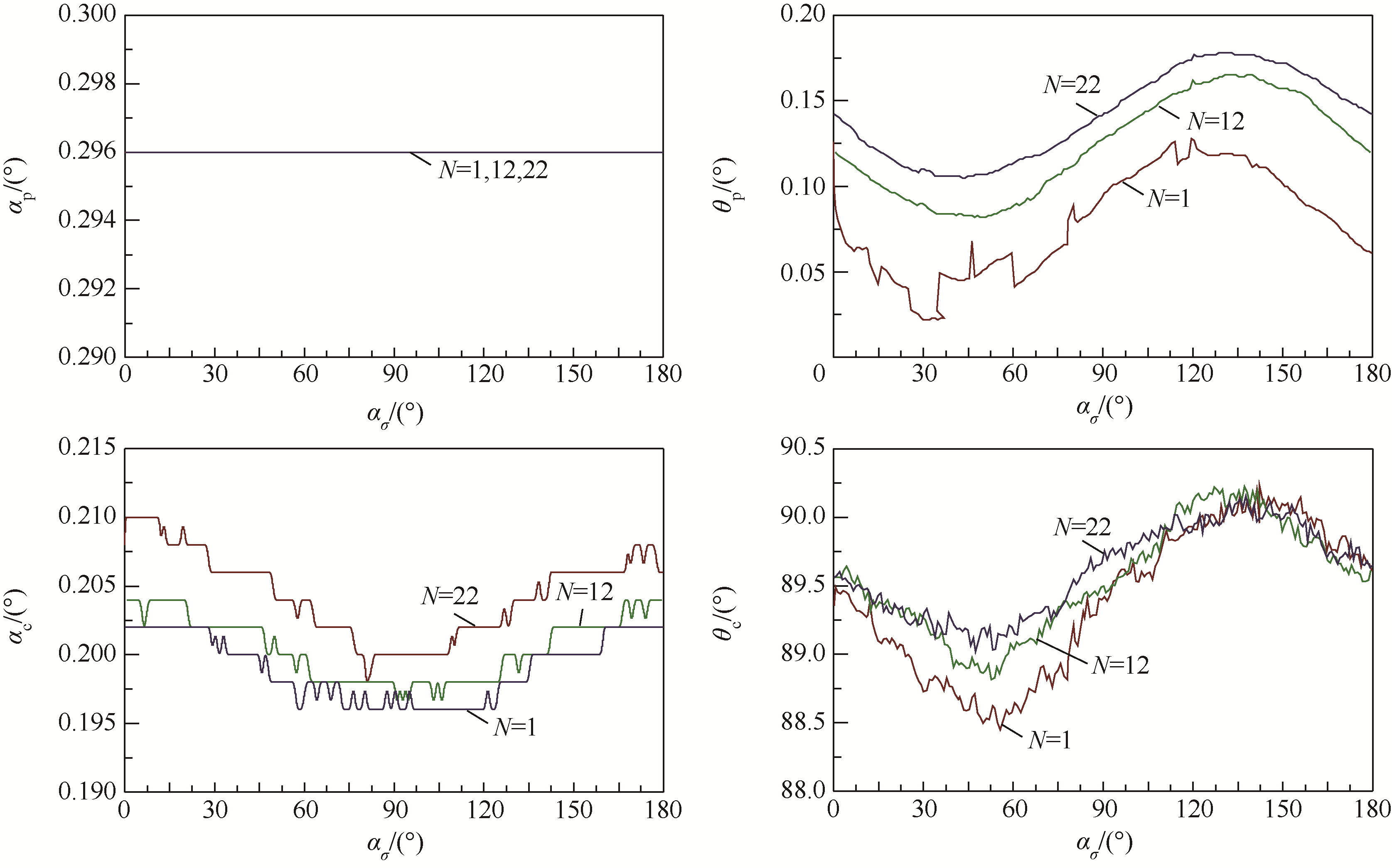 |
| 图 7 颗粒组构特征在一个周期内的变化规律Fig. 7 Evolution of fabric properties of granules in a single cycle |
图 8所示为配位数的变化规律.由图 8可知,配位数在单个循环周内变化幅度较小,随循环周数增加而增加,这表明颗粒材料在应力主轴循环旋转过程中不断硬化.
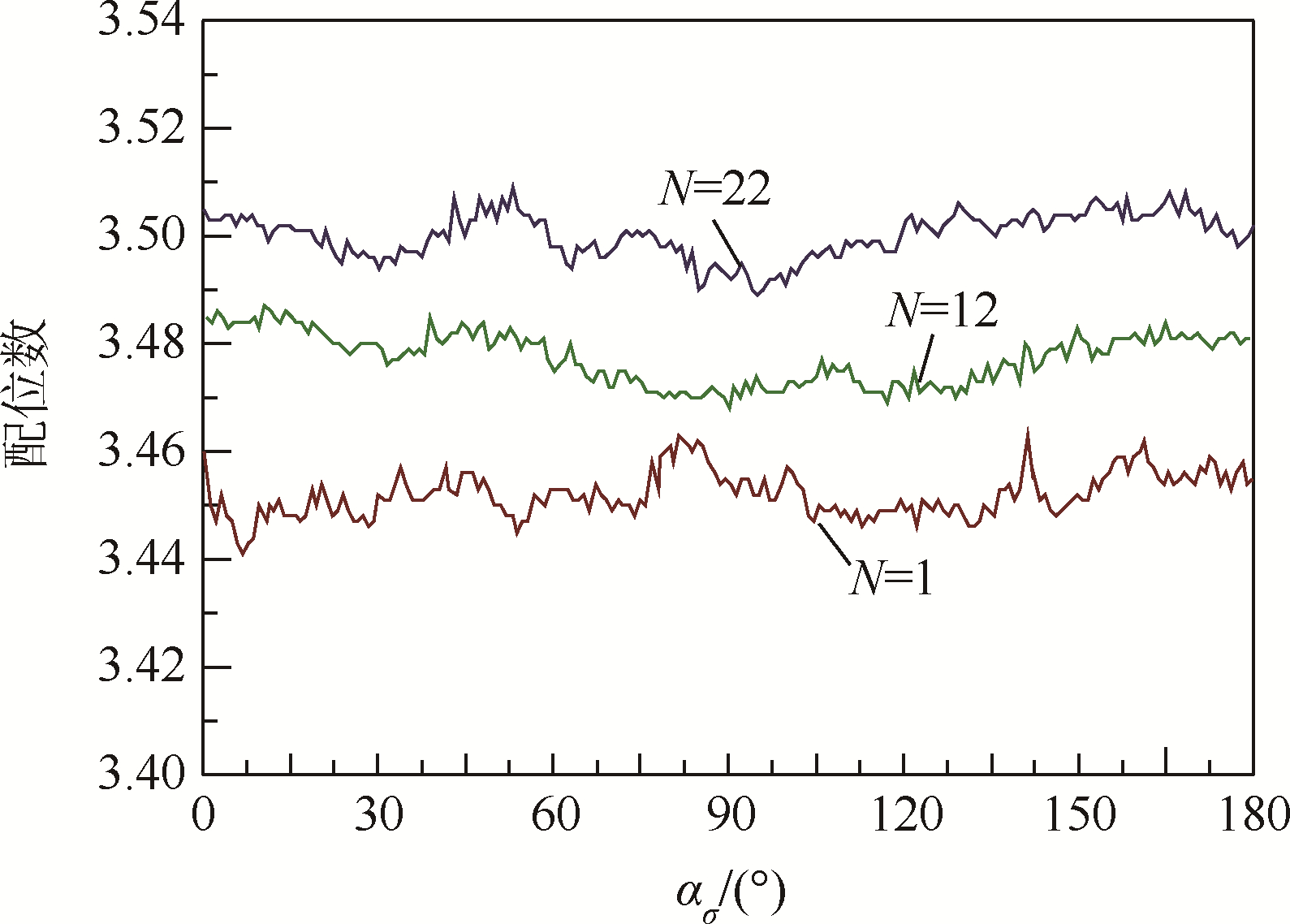 |
| 图 8 配位数在一个周期内的变化规律Fig. 8 Evolution of coordination number in a single cycle |
以粒间接触法线组构张量的特征变量αc和θc为例,图 9和图 10分别给出了初始孔隙比相同、应力比不同以及应力比相同、初始孔隙比不同2种情况下αc和θc随循环周数的变化规律.分析图 9和图 10可知,应力比越大,αc越大,即粒间接
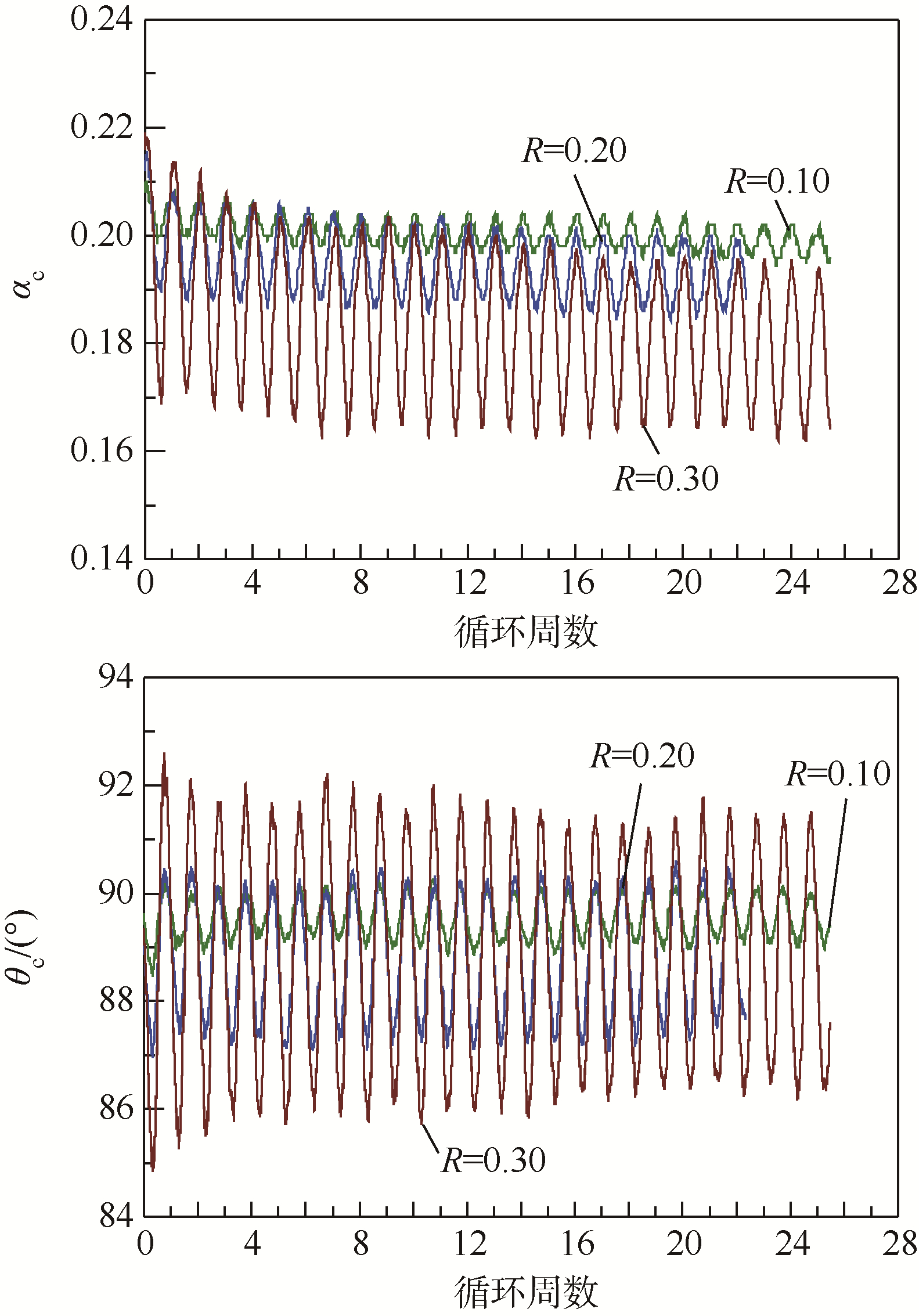 |
| 图 9 应力比对αc和θc的影响(e0=0.251)Fig. 9 Effects of stress ratio on αc and θc(e0=0.251) |
 |
| 图 10 初始孔隙比对αc和θc的影响(R=0.3)Fig. 10 Effects of initial void ratio on αc and θc(R=0.3) |
触法线分布的各向异性程度更强;同时粒间接触法线角θc的变化幅度亦随应力比的增大而增加.当试样初始孔隙比不同,而施加的应力比相同时,初始孔隙比主要影响前几个循环周的αc和θc;试样密度越松,αc和θc的变化幅度越大;但随着循环周数的增加,αc和θc的变化幅度趋向于相同,与初始孔隙比关系不大.
4 结 论应力主轴旋转条件下砂土的变形特性复杂,其宏观力学响应与细观组构及其演化规律密切相关.本文通过将数值模拟与物理试验在正应变分量发展、剪应力-剪应变关系曲线、体应变发展规律及影响因素等方面进行对比分析,在验证离散元数值模拟有效性的基础上,对应力主轴旋转条件下颗粒材料的细观组构演化规律进行了初步探索,得到以下主要结论.
1) 颗粒长轴定向组构在应力主轴循环旋转过程中基本无变化,这表明颗粒长轴定向引起的试样固有各向异性对应力主轴旋转条件下的力学特性有重要影响.
2) 粒间接触法线分布的各向异性程度在单个循环周内呈余弦式变化规律,其变化幅度随循环周数增加有增大的趋势.
3) 粒间接触法线角度θc在单个循环周内呈正弦式变化;随循环周数增加,θc的变化幅度呈递减趋势,但远小于应力主轴旋转幅度.
4) 粒间接触法线分布的各向异性程度及法线角度θc均随应力比的增大而增加.在应力比相同的条件下,试样初始孔隙比主要对前几个循环周次的粒间接触法线组构有影响;随循环周数的增加,初始孔隙比不同的试样趋近于达到相同的粒间接触法线组构.
致谢 感谢Lawrence Livermore National Laboratory的付鹏程博士在数值模拟中给予作者的大力帮助!
| [1] | Ishihara K, Towhata K.Sand response to cyclic rotation of principal stress directions as induced by wave loads[J].Soils and Foundations, 1983, 23(4):11-26. |
| Click to display the text | |
| [2] | Symes M J, Gens A, Hight D W.Undrained anisotropy and principal stress rotation in saturated sand[J].Geotechnique, 1984, 34(1):11-27. |
| Click to display the text | |
| [3] | Syme M J, Gens A, Hight D W.Drained principal stress rotation in saturated sand[J].Geotechnique, 1988, 38(1):59-81. |
| Click to display the text | |
| [4] | Miura K, Miura S, Toki S.Deformation behavior of anisotropic sand under principal stress axes rotation[J].Soils and Foundations, 1986, 26(1):36-52. |
| Click to display the text | |
| [5] | Gutierrez M, Ishihara K, Towhata I.Flow theory for sand during rotation of principal stress direction[J].Soils and Foundations, 1991, 31(4):121-132. |
| Click to display the text | |
| [6] | Nakata Y, Hyodo M, Murata H, et al.Flow deformation of sands subjected to principal stress rotation[J].Soils and Foundations, 1998, 38(2):115-128. |
| Click to display the text | |
| [7] | 郭莹, 栾茂田, 何杨, 等.主应力方向循环变化对饱和松砂不排水动力特性的影响[J].岩土工程学报, 2005, 27(4):403-409. Guo Y, Luan M T, He Y, et al.Effect of variation of principal stress orientation during cyclic loading on undrained dynamic behavior of saturated loose sands[J].Chinese Journal of Geotechnical Engineering, 2005, 27(4):403-409(in Chinese). |
| Cited By in Cnki (49) | |
| [8] | Yang Z X, Li X S, Yang J.Undrained anisotropy and rotational shear in granular soil[J].Geotechnique, 2007, 57(4):371-384. |
| Click to display the text | |
| [9] | Zhang J M, Tong Z X, Yu Y L.Effects of cyclic rotation of principal stress axes and intermediate principal stress parameter on the deformation behavior of sands[C]//Geotechnical Earthquake Engineering and Soil Dynamics IV Congress 2008-Geotechnical Earthquake Engineering and Soil Dynamics.Reston:American Society of Civil Engineers, 2008:181. |
| [10] | 童朝霞, 于艺林, 张建民, 等.中主应力系数对应力主轴循环旋转条件下砂土变形特性的影响[J].岩土工程学报, 2009, 31(6):946-952. Tong Z X, Yu Y L, Zhang J M, et al.Effects of intermediate principal stress parameter on deformation behavior of sands under cyclic rotation of principal stress axes[J].Chinese Journal of Geotechnical Engineering, 2009, 31(6):946-952(in Chinese). |
| Cited By in Cnki (13) | |
| [11] | Tong Z X, Zhang J M, Yu Y L, et al.Drained deformation behavior of anisotropic sands during cyclic rotation of principal stress axes[J].Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(11):1509-1518. |
| Click to display the text | |
| [12] | Li X, Yu H S.Numerical investigation of granular material behavior under rotational shear[J].Geotechnique, 2010, 60(5):381-394. |
| Click to display the text | |
| [13] | Fu P C, Dafalias Y F.Study of anisotropic shear strength of granular materials using DEM simulation[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(10):1098-1126. |
| Click to display the text | |
| [14] | Fu P C, Dafalias Y F.Fabric evolution within shear bands of granular materials and its relation to critical state theory[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(18):1918-1948. |
| Click to display the text | |
| [15] | Oda M, Iwashita K.Mechanics of granular materials:an introduction[M].Rotterdam:A A Balkma Publishers, 1999:1-100. |
| Click to display the text |



