在系统辨识领域,模型定阶一直以来都是方法论研究者和应用工程师无法回避的问题,在实验模态分析领域也不例外[1].实际的模态参数辨识中,无论是时域方法还是频域方法,所对应参数化模型的阶数都是未知的.模型阶数太低会导致无法有效地辨识出所需的模态参数;阶数太高可能过拟合,出现众多的虚假模态,甚至影响真实物理模态的辨识质量.
在实验模态分析领域,通常在给定范围内改变模型阶数,得到不同阶数对应的模态参数,进一步通过某些特定准则完成模态参数验证,其中,稳定图是一种常用工具[2],并有学者对此进行了深入研究[3].然而,稳定图自身并不能解决模态参数验证问题,仅作为工具帮助使用者进行人工选取.对于真实复杂结构,人工选取工作量大且依赖使用者的主观意识和经验.
最近,已有学者对模态参数的自动验证方法展开了研究.Lanslots等[4]提出了一种从稳定图自动选择极点的方法,该方法通过模拟有经验人员的选取方法对稳定图进行分析,但是这需要大量专家经验,本质上仍是一种直接选取的方法.孙国富[5]提出了一种基于模糊聚类分析的自动模态参数验证方法,将模态频率、阻尼比和模态振型综合为一个统一的数据点进行模糊聚类,并以此验证模态参数;这种方法直接给定各模态参数在总的距离函数中的权值,而权值的选取仍然是无法自动完成的.Reynders等[6]提出了基于层次聚类的三阶段验证方法,将模态频率和阻尼比作为数据进行聚类并完成模态参数验证.
本研究利用先进的数据挖掘数学工具——模糊聚类分析,并考虑所有模态参数(模态频率、阻尼比、模态参与因子和模态振型),提出自动的模态参数验证方法:将模态参数分为标量型和向量型两类,采用传统的模糊聚类方法对标量型模态参数进行聚类分析;然后提出一种基于模态置信准则的距离函数,实现模态振型的模糊聚类;最后综合标量型和向量型模态参数模糊聚类的结果,完成模态参数的全因素自动验证方法.通过弹翼模态实验结果对所提出的方法进行了验证.
1 模糊聚类
聚类分析(cluster analysis)的目的是将一组含有物理信息或抽象信息的数据集合分入若干个聚类(cluster)中,较之不同聚类中的数据,处于同一聚类中的数据彼此间具有更多的相似性.将模糊聚类分析引入模态分析领域,旨在利用模糊聚类分析来验证和筛选辨识得到的时变结构模态参数.
经过多年的发展,出现了许多聚类分析方法,如层次聚类、划分聚类及模糊聚类等[7],其中,模糊聚类已经被广泛地运用于各种领域,如面部识别[8]、图像分割[9]及信号分析[10]等.不同于传统的聚类分析方法,模糊聚类是用隶属度将数据与聚类联系起来的,即用隶属度来表示数据属于某给定聚类的程度.
模糊聚类是将一组数据按照其隶属度分入C个聚类中,每一聚类用其中心来表示,模糊聚类的中心称为聚类的原型.换句话说,模糊聚类的目标是找到各个聚类的原型以及数据对各原型的隶属度.
令X={x1,x2,…,xN}Rp为一个含有N∈Ν1个元素的数据集合(其中Rp表示p维的实数集,Ν1为一维的自然数集,下同).用U∈RC×N表示N∈Ν1个元素的数据集合对C∈Ν1个聚类的隶属度矩阵.U∈RC×N中的元素uij(i=1,2,…,C;j=1,2,…,N)表示第j个元素隶属于第i个聚类相对于其他聚类的程度.由于模糊聚类中的隶属度矩阵U∈RC×N表示的是一种概率的聚类划分,因此对于U∈RC×N有如下的约束:

令V={v1,v2,…,vC} ⊂ Rp表示由C∈Ν1个聚类原型组成的聚类原型集合,其中vi为第i个聚类的原型.
模糊c均值算法(Fuzzy c-Means,FCM)[11]是模糊聚类分析中最为常见的一种算法,同时也是一种基于目标函数的模糊聚类算法.若给定数据集合X,隶属度矩阵U,聚类原型集合V和距离函数d,那么一个标量的目标函数可描述为
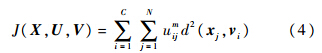

2 模态参数验证
为完成模态参数的自动验证,将模态参数分为两类:标量型模态参数和向量型模态参数.其中,标量型模态参数包括模态频率、模态阻尼比和模态参与因子(虽然模态参与因子也是向量,但是一般模态实验的参考点数为1~2个,因此将模态参与因子列入标量型模态参数进行考虑);向量型模态参数包括模态振型.分别对标量型和向量型模态参数进行模糊聚类,根据模糊聚类中心对应的最近数据点,综合两类模态参数的聚类结果,提出模态参数的自动验证方法.
2.1 标量型模态参数的模糊聚类
通过模态参数辨识,可以获取不同模型阶数对应的模态参数,假设共有N组,每一组(第j组)包括模态频率fj、模态阻尼比ξj、模态参与因子Lj和模态振型φj,其中,不失一般性,设单参考的情况,即模态参与因子为一标量.
若设标量型模态参数对应的单个数据为sj=[fj ξj Lj],那么,标量型的模态参数数据集为S={s1,s2,…,sN}.给定聚类个数Cs,采用第1节所述的FCM方法对此数据集进行模糊聚类,其中,距离函数为式(5)定义的欧氏距离函数.可得到Cs个聚类,用聚类原型表示为
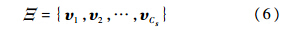
为实现后面的两类模态参数的综合交叉验证,根据聚类原型,找出各原型对应的距离最近的数据点,定义为
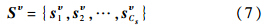
2.2 向量型参数(振型)的模糊聚类
同样,按照标量型模态参数的模糊聚类也可以对模态振型进行聚类,得到一组如式(7)所示的聚类结果.然而,每一个模态振型向量都含有多个分量(一个振型下每一个自由度对应一个振型分量).通常为了捕捉足够多的模态数,测点至少需要十几个,甚至几十上百个,这就意味着模态振型向量φj是一个高维的数据点.对于高维数据,采用欧氏距离函数进行聚类,会无法避免地带来困难,如聚类中心趋同、隶属度平均化等[12].另外,对于复模态分析,模态振型向量各个分量都为复数,不便于定义两个振型向量的欧氏距离.因此,为了实现模态振型向量这样的复数高维数据的模糊聚类,需发展特殊的距离函数.
通常,模态分析领域的学者利用模态置信准则[13](MAC)来描述两个模态振型向量的相似性,相似性越高MAC值越大,相似性越低MAC值越小,两个相同的模态振型向量的MAC值为1,两个完全正交的模态振型向量的MAC值为0.根据MAC的定义[2]发现,两个向量之间的角度θ可以写为
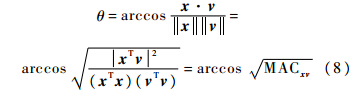
容易发现θ定义在区间[0,π/2]上.为了增大不相似振型之间的“距离”,对式(8)定义的角度实施进一步改进,定义如下的距离函数:

不难证明,d′满足“距离”的定义,是一个数学意义上的距离函数,并且d′的取值范围在区间[0,∞)上,可以显著地区分两个不相似的振型向量,提高不同聚类之间的分离性.
以类似于对标量型模态参数的处理定义模态振型的数据集Φ={φ1,φ2,…,φN}.给定聚类个数Cφ,采用距离函数d,对此数据集进行模糊聚类,得到Cφ个聚类原型,并根据距离函数d′找出各原型对应距离最近的数据点,定义为

2.3 两类模态参数的综合交叉验证
通过对标量型和向量型模态参数分别进行模糊聚类得到了对应的数据集合,这些集合中的数据点潜在地描述了不同阶模态,但是由于数据点个数为预先给定的聚类个数,包含了一定数量的虚假模态,因此需要对聚类结果进一步分析挖掘,建立两类模态参数的综合交叉验证方法.
为方面起见,将N组模态参数进行统一编号,定义N组模态参数的编号集:

那么,可以定义标量型模态参数聚类结果(如式(7)所示)对应的编号集和模态振型聚类结果(如式(10)所示)对应的编号集,分别为
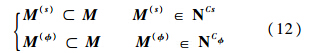
根据编号集M(s)和M(φ)可从N组模态参数构成的模态参数总集中取出相应的模态参数,分别构成模态频率、模态阻尼比、模态参与因子和模态振型的各两个集合:f(s)和f(φ)、ξ(s)和ξ(φ)、L(s)和L(φ)、Φ(s)和Φ(φ).
设p=1,2,…,Cs、q=1,2,…,Cφ,定义两类聚类结果交叉验证的模态频率、模态阻尼比、模态参与因子和模态振型的布尔矩阵Bf、Bξ、BL和Bφ的元素Bf,pq、Bξ,pq、BL,pq和Bφ,pq分别为
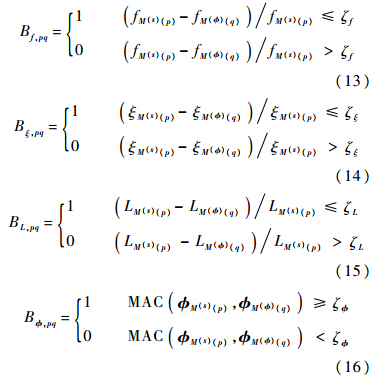
若得到各参数交叉验证的布尔矩阵,即可利用布尔矩阵元素的布尔和对模态参数进行全因素的综合验证,定义综合验证的布尔矩阵元素:

综合验证布尔矩阵B的列标可以定位最终验证得到模态参数组的总体编号,从而得到完成验证的模态参数集合.
3 实验验证
实验结构为如图 1所示弹翼结构,结构形式为典型的整体加筋壁板,材料为镁铝合金,质量为5.343 kg,最长处为1 780 mm.
 |
| 图 1 弹翼实验件Fig. 1 Test rig of a sample wing |
采用标准的模态实验实施方法,用橡皮绳将实验件竖直悬挂以模拟自由-自由的边界条件,激励方式为锤击,在弹翼表面布置30个单轴的加速度传感器(测量方向为垂直于弹翼表面,测点布置如图 2所示),激励和响应信号采样频率为128 Hz,频率分辨率为0.125 Hz.实验设备包括LMS SCADAS III数采系统、PCB333B30加速度计及PCB208C03力锤;数据采集软件为LMS Testlab.
 |
| 图 2 测点布置Fig. 2 Deployment of measurement locations |
频率响应函数参考点(激励)为位于图 2左下角点处,原点频率响应函数如图 3所示(1.9 Hz处的峰由悬挂系统弹性引起).
 |
| 图 3 原点频率响应函数Fig. 3 Origin frequency response function |
模态参数辨识采用最小二乘复频域法(LSCF)[14],辨识频带为0~64 Hz,辨识数据为30个响应点对激励点的频率响应函数.阶数从10取到32,共得到483组模态参数,去除负频率和负阻尼比以及阻尼比大于10%的模态,共有N=250组模态参数用于验证.采用2.1节提出的方法对标量型进行模糊聚类,得到结果如图 4所示.
 |
| 图 4 模糊聚类结果Fig. 4 Fuzzy clustering results |
根据图 4所示的模糊聚类的结果,采用2.3节提出的综合验证方法对辨识得到的模态参数进行验证,即:首先根据图 4所示的原型最近点获取编号集;然后,分别列出f(s)和f(φ)、ξ(s)和ξ(φ)、L(s)和L(φ)、Φ(s)和Φ(φ).根据集合,给定ζf=0.01,ζξ=0.05,ζL=0.02,ζφ=0.95,采用式(13)~式(16)构建布尔矩阵,如图 5所示.
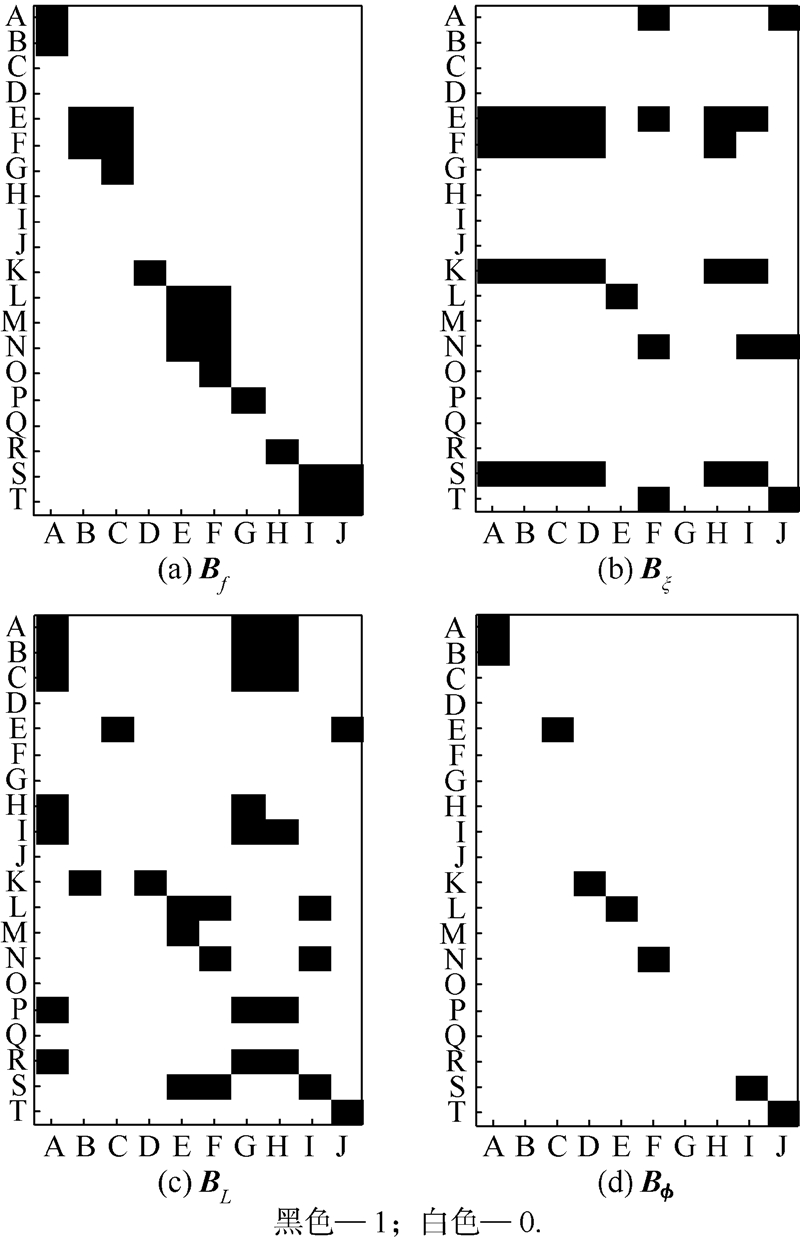 |
| 图 5 布尔矩阵Fig. 5 Boolean matrix |
最后,根据图 5所示的布尔矩阵和式(17)得到最终验证的模态参数.最终验证的模态参数如表 1所示,验证后的振型对应的MAC矩阵如图 6所示.
| 模态阶数 | 频率/Hz | 阻尼比/% | 辨识模型阶数 | 在总集合中序号 |
| 1 | 24.65 | 0.23 | 19 | 86 |
| 2 | 36.73 | 0.21 | 22 | 121 |
| 3 | 44.73 | 0.60 | 23 | 139 |
| 4 | 45.08 | 0.30 | 26 | 166 |
| 5 | 59.94 | 0.26 | 13 | 29 |
| 6 | 60.35 | 0.31 | 30 | 212 |
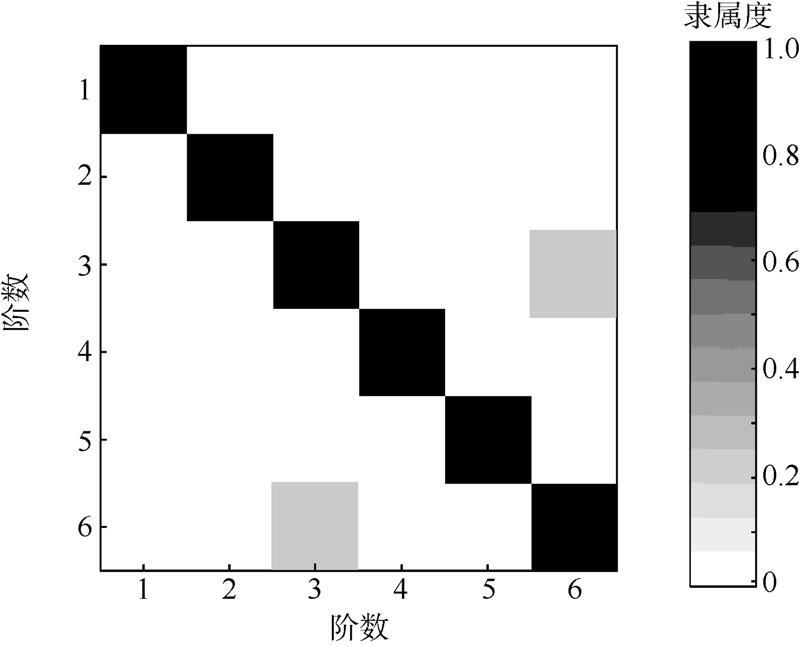 |
| 图 6 验证后振型的MAC矩阵Fig. 6 MAC matrix of validated mode shapes |
由表 1可知,通过提出的模态参数验证方法可以很好地自动得到频带内结构的全部6阶模态.由图 6可知,通过验证的模态参数具有很好的正交性(测点基本上是均匀分布的).
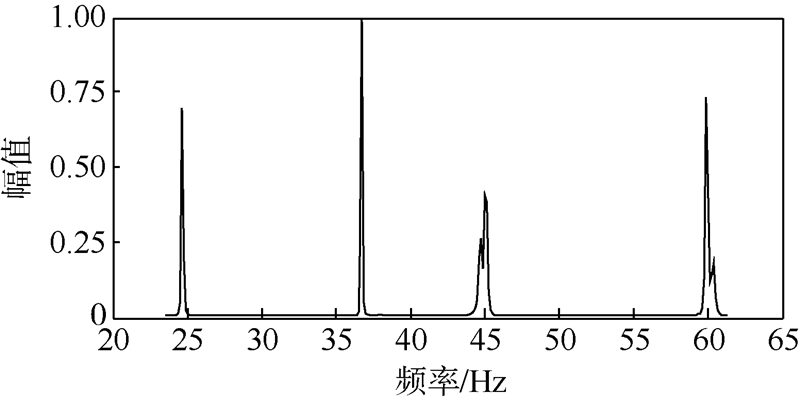
另外,通过辨识并验证后的模态参数综合的激励点原点频率响应函数如图 3中实线所示,峰值附近与测量的频率响应函数一致,也说明了本方法的有效性.由图 3可知,在频带内除悬挂导致的1.9 Hz处的峰外共有4个峰,但是通过辨识并验证得到了6阶模态.那么,在45 Hz和60 Hz可能出现了密频模态或虚假模态.为排除是虚假模态的可能,可通过两方面加以说明:一方面,图 6的MAC矩阵的正交检验说明45 Hz附近和60 Hz附近的4阶模态是正交的;另一方面,图 7中模态指示函数(MIF)[15]的虚部在45 Hz附近和60 Hz附近各出现了两个波谷,这是因为频率响应函数峰值受到模态参与因子的影响,参与因子较低的模态在参与因子较大的模态附近时可能被后者掩盖,而模态指示函数则可以克服这个问题.分析结果表明并未出现虚假模态.
4 结 论
提出了一种基于模糊聚类分析、考虑所有模态参数(模态频率、阻尼比、模态参与因子和模态振型)的模态参数验证方法,得到以下结论.
1) 方法考虑全部模态参数,最大化地使用辨识得到的信息,能够很好地去除虚假数学模型,且不易遗漏真实物理模态.
2) 在处理振型的模糊聚类时,为了解决高维和复数问题,提出了一种基于MAC的距离函数.
3) 验证实验结果表明,方法能够自动验证结构模态辨识得到的模态参数,且实施较为简单,不依赖使用者的经验.
| [1] | 姚竹亭,潘宏侠.装甲车辆齿轮主传动系统的建模与辨识[J].振动、测试与诊断,2005,25(3):33-36. Yao Z T,Pan H X.Study on modeling and identification of main transmission system in armored vehicle[J].Journal of Vibration,Measurement & Diagnosis,2005,25(3):33-36(in Chinese). |
| Cited By in Cnki (2) | |
| [2] | Heylen W,Lammens S,Sas P.Modal analysis theory and testing[M].Belgium,Leuven:Katholieke Universiteit Leuven,2007:B.4.9-B.4.10. |
| [3] | 杨毅青,刘强,Munoa J.基于正交多项式和稳定图的密集模态参数辨识[J].振动、测试与诊断,2010,30(4):429-433. Yang Y Q,Liu Q,Munoa J.Modal parameter identification of closely-coupled modes based on orthogonal polynomial and stabilization diagram[J].Journal of Vibration,Measurement & Diagnosis,2010,30(4):429-433(in Chinese). |
| Cited By in Cnki (5) | |
| [4] | Lanslots J,Rodiers B,Peeters B.Automated pole-selection:proof-of-concept & validation[C]//Proceedings of the ISMA International Conference on Noise and Vibration Engineering.Belgium,Leuven:Katholieke Universiteit Leuven,2004:1005-1018. |
| Click to display the text | |
| [5] | 孙国富.基于模糊聚类的模态参数自动识别[J].振动与冲击,2010,29(9):86-88. Sun G F.Automatic modal parameters identification based on fuzzy clustering[J].Journal of Vibration and Shock,2010,29(9): 86-88(in Chinese). |
| Cited By in Cnki (5) | |
| [6] | Reynders E,Houbrechts J,de Roeck G.Fully automated (operational) modal analysis[J].Mechanical Systems and Signal Processing,2012,29:228-250. |
| Click to display the text | |
| [7] | Jain A K,Murty M N,Flynn P J.Data clustering: a review[J].ACM Computing Surveys,1999,31(3):264-323. |
| Click to display the text | |
| [8] | Lu J,Yuan X,Yahagi T.A method of face recognition based on fuzzy clustering and parallel neural networks[J].Signal Processing,2006,86(8):2026-2039. |
| Click to display the text | |
| [9] | Cinque L,Foresti G,Lombardi L.A clustering fuzzy approach for image segmentation[J].Pattern Recognition,2004,37(9):1797-1807. |
| Click to display the text | |
| [10] | Łęski J M,Owczarek A J.A time-domain-constrained fuzzy clustering method and its application to signal analysis[J].Fuzzy Sets and Systems,2005,155(2):165-190. |
| Click to display the text | |
| [11] | Hoppner F,Klawonn F,Kruse R,et al.Fuzzy cluster analysis:methods for classification,data analysis and image recognition[M].Chichester,West Sussex:John Wiley & Sons Ltd,1999:37-42. |
| [12] | Winkler R,Klawonn F,Kruse R.Problems of fuzzy c-means clustering and similar algorithms with high dimensional data sets[M].Berlin:Springer,2012:79-87. |
| [13] | Allemang R J.The modal assurance criterion(MAC):twenty years of use and abuse[J].Sound and Vibration,2003,37(8):14-23. |
| [14] | van der Auweraer H,Guillaume P,Verboven P,et al.Application of a fast-stabilizing frequency domain parameter estimation method[J].Journal of Dynamic Systems,Measurement,and Control,2001,123(4):651-658. |
| Click to display the text | |
| [15] | Avitabile P.Modal space:The stability diagram has poles that are not indicated by the mmif or cmif;are they really modes?[J].Experimental Techniques,2007,31(5):17-18. |
| Click to display the text |