符号数据分析(SDA)可以对海量巨维数据的分析提供行之有效的解决思路,因而成为目前统计学研究的前沿领域,具有众多的理论研究成果和广泛的实际应用案例[1, 2, 3, 4].区间数据作为一种符号数据,因其具有广泛的应用价值而得到关注[5, 6].尤其在面对海量数据时,采用区间数据可以极大地约简原始数据,进而基于区间数据分析的方法进行数据处理[7, 8, 9].
区间数据分析的众多研究文献,无论是采用顶点法、均值法还是引入内积运算、平方范数等,都是基于数据在某一个闭区间(或紧致集合)上服从均匀分布的假定,且区间数据分析的理论性质均基于此假定.而在实际数据处理中,假设数据来源于某一固定区间,并且在该区间上服从均匀分布,通常是难以满足的.例如在统计学处理中,通常会假设数据服从正态分布而不是均匀分布.一旦均匀分布这一假定不满足,其良好的理论性质均不再成立.因此,均匀分布这一假定在区间数据分析中起着基础性的重要作用,需要对区间数据分析的这一假定进行重新审视,并在数据不服从均匀分布时给出合理化的解决方法[10, 11].
基于以上考虑,仅假定原始数据来源于某一连续分布,本文提出一种基于数据驱动的变换,对原始数据进行该变换后,从理论上证明在样本容量足够大时其服从均匀分布,在实际数据处理操作中可对其是否服从均匀分布进行假设检验,进而可采用已有的区间数据分析方法进行后续分析,如主成分分析、回归分析等.数据模拟的结果可以看出,经过变换后的数据基本可以通过假设检验,即使是在样本量较小的情形下.
1 基于经验分布函数的变换本节从最简单的情形出发,基于经验分布函数给出数据变换公式.
设X为服从某一连续分布的随机变量,(x1,x2,…,xn)是已得到的一组样本数据,将其转化为区间数据的方法是取其最大值和最小值作为区间的两个端点,假定其他样本在这个区间服从均匀分布[5].这一假定明显过于严格,如果样本服从其他分布,会导致这一假定及其后续分析的结果失效.
令X的分布函数为F(t),经验分布函数Fn(t)定义为
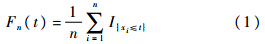
设随机变量F(X)的分布函数为H,则有
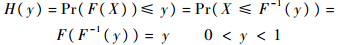
从以上分析可知,对于原始数据(x1,x2,…,xn)可以通过式(3)的变换得到(z1,z2,…,zn),转化为理论上服从(0,1)均匀分布的区间数据进行后续的处理和分析.
这里使用经验分布函数对真实的分布函数进行估计,但经验分布函数不是可逆的,可以考虑采用其他估计量.例如在单调约束下采用核方法等非参数方法进行估计,在一定光滑性条件下保证得到的估计量具有逆函数,从而保证变换是可逆的.直接对分布函数F(t)进行估计,需要考虑单调约束;如果转化为估计密度函数f(t),则不需要在单调约束条件下进行估计,并且密度估计具有较多的已有成果可以借鉴,这里考虑核密度估计方法[12],之后通过积分变换得到分布函数的估计量.
将式(1)换一种表达形式为
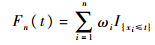
首先给出核密度估计:
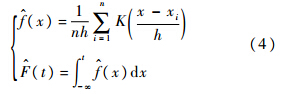
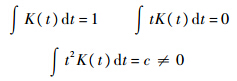
(x)非负,所以估计得到的
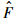(t)具有单调性,因而这是个可逆变换.在使用核方法进行估计时,核函数的选择并不关键,重要的是要对窗宽h进行选择.这里采用基于似然函数的交叉验证指标:
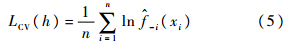
-i表示去掉第i个样本之后得到的核密度估计.最终选择使得LCV(h)取最大值的h作为窗宽.在式(4)中,积分区域是从无穷开始的.在实际估计中,选择某个距离样本点的极小值x(1)较远的数值即可.
2 变换后的假设检验第1节中本文基于经验分布函数构造了变换,本节讨论对变换后的数据进行是否服从均匀分布的假设检验.
考虑如下假设检验问题:
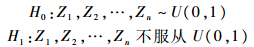
针对数据是否服从某一给定分布的假设检验问题,文献中有着较多的检验统计量,基本上分为基于经验分布函数的、基于次序统计量的和基于距离的3种[14],包括常见的Kolmogorov-Smirnov统计量[15]、Anderson-Darling统计量[16]、Cramér-von Mises统计量[17]等.文献[18]提出了式(6)和式(7)的统计量,与常见的统计量相比具有较高的功效,因此这里采用该统计量.
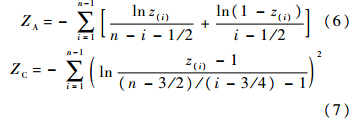
注意到,经过变换后的数据均分布在(0,1)上,从而不需要估计均匀分布所在区间的端点值.实际上,文献中通常是采用最小值和最大值来作为区间端点的估计值.在均匀分布情形下可以证明,最小值和最大值并非区间端点的无偏估计量.本文的方法避免了这一偏差的存在.
3 基于变换数据的区间数据分析
本节将原始数据经过变换后得到的数据整理成区间数据表,以便进行后续分析.
根据原始数据定义数据矩阵如下：
定义
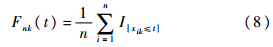
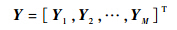
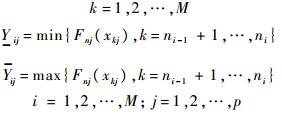
这时得到的数据表为 Y ,是个典型的区间数据表,基于此可以进行主成分、回归分析等.
经过变换后得到的区间数据所有的取值都落在0~1之间.从数据信息的角度考虑,所做变换相当于对原始数据进行了方差压缩,消除了不同变量量纲不同的影响.
类似于经验分布函数变换,也可以对数据进行基于核估计函数的变换,然后整理成区间数据表.
4 数据模拟 4.1 数据模拟1本节讨论在不同样本容量下,取自不同分布(正态分布N(0,1)、指数分布Exp(2)、柯西分布Cauchy和均匀分布U(0,1),U(5,10))的样本,经过变换后是否能通过均匀分布检验,采用第2节中提到的统计量.表 1是模拟的结果.每组模拟进行1 000次,计算原假设不被拒绝的频率(在0.05的水平下),采用的统计量是ZA.
| 样本量 | N(0,1) | Exp(2) | Cauchy | U(0,1) | U(5,10) |
| 5 | 0.115 | 0.086 | 0.052 | 0.865 | 0.878 |
| 10 | 0.035 | 0.012 | 0.004 | 0.934 | 0.925 |
| 20 | 0.006 | 0.002 | 0 | 0.965 | 0.951 |
| 40 | 0.002 | 0 | 0 | 0.949 | 0.948 |
| 50 | 0 | 0 | 0 | 0.957 | 0.955 |
| 100 | 0 | 0 | 0 | 0.972 | 0.952 |
| 200 | 0 | 0 | 0 | 0.956 | 0.947 |
由表 1的结果可知,如果数据本身来源于某些不是均匀分布的常见分布,进行假设检验时很难认为其服从均匀分布;只有当原始数据来源于均匀分布时,可以在一定水平下不能拒绝其来自于均匀分布.而采用经过变换后的数据时,数据都成为样本容量倒数的整数倍,因而可以通过检验,是来自均匀分布的.
4.2 数据模拟2
笔者在不同分布中分别采用经验分布函数和核估计方法对分布函数进行估计,具体结果如图 1所示.这里所适用的样本容量是50.样本容量为50时,二者都较好地拟合了分布函数.随着样本容量增大,二者对分布函数的拟合都具有较好效果.经验分布函数是阶梯函数,比较粗糙,而分布函数的核估计则相对光滑.
 |
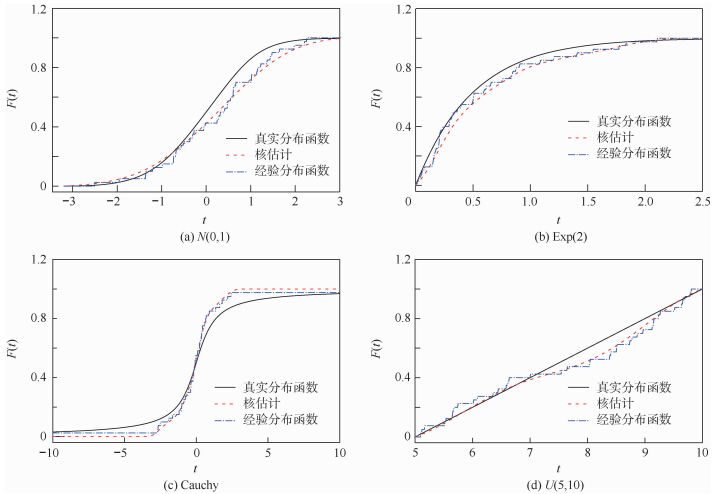| 图 1 对不同分布的分布函数分别采用经验分布函数和核方法进行估计的结果Fig. 1 Simulation results for estimating the cumulative distribution function by empirical distribution and kernel method |
表 2给出了利用经验分布函数和核方法对分布函数进行估计的偏差.在模拟中,随着样本容量的增大,两种估计的偏差都在不断减小,但核方法在区间端点处对分布函数的估计效果略差.在数据来源于重尾分布(表 2中所示的Cauchy分布)时,两种估计的偏差相对都较大.
| 分布类型 | 样本量20 | 样本量50 | 样本量100 | 样本量200 | ||||
| 经验分布 | 核估计 | 经验分布 | 核估计 | 经验分布 | 核估计 | 经验分布 | 核估计 | |
| N(0,1) | 0.247 6 | 0.197 8 | 0.180 6 | 0.164 9 | 0.171 4 | 0.126 4 | 0.096 4 | 0.081 9 |
| Exp(2) | 0.180 3 | 0.168 0 | 0.152 5 | 0.136 8 | 0.092 1 | 0.109 4 | 0.026 4 | 0.029 5 |
| Cauchy | 0.626 1 | 0.552 0 | 0.526 1 | 0.546 5 | 0.472 6 | 0.585 9 | 0.226 7 | 0.407 0 |
| U(2,3) | 0.086 0 | 0.079 3 | 0.057 6 | 0.040 1 | 0.028 6 | 0.020 5 | 0.011 9 | 0.016 1 |
| U(5,10) | 0.274 5 | 0.222 0 | 0.204 4 | 0.195 8 | 0.190 7 | 0.140 9 | 0.159 8 | 0.153 8 |
本文针对区间数据分析中的均匀分布基本假定在实际数据分析中往往得不到满足的情况,提出一种利用连续型随机变量的性质,依赖经验分布函数和核估计方法对其分布函数进行估计,从而构造了两种数据变换,使得经过变换后的数据满足均匀分布的假设.因此,在使用区间数据分析方法前,应先对数据是否服从均匀分布进行假设检验,若无法通过检验则考虑对数据进行变换,本文基于经验分布函数给出了这样的变换.以变换后的数据作为分析对象,进行后续的区间数据分析更加合理.所提出的变换可推广到使用区间数据分析方法的数据预处理中,使得已有的分析方法更加严谨.
进行变换后的数据满足均匀分布的假设,可进行主成分分析、聚类分析、回归分析等,这是下一步的研究工作.
| [1] | Sankararaman S, Mahadevan S.Likelihood-based representation of epistemic uncertainty due to sparse point data and/or interval data[J].Reliability Engineering & System Safety,2011,96(7):814-824. |
| Click to display the text | |
| [2] | Diday E, Noirhomme-Fraiture M.Symbolic data analysis and the SODAS software[M].London:Wiley Online Library,2008:81-92. |
| [3] | Billard L. Symbolic data analysis:what is it?[M].New York:Springer,2006:261-268. |
| [4] | Diday E, Esposito F.An introduction to symbollic data analysis and the SODAS software[J].Intelligent Data Analysis,2003,7(6): 583-601. |
| Click to display the text | |
| [5] | Wang H W, Guan R,Wu J J.CIPCA:complete-information-based principal component analysis for interval-valued data[J].Neurocomputing,2012,86:158-169. |
| Click to display the text | |
| [6] | Wang H W, Guan R,Wu J J.Linear regression of interval-valued data based on complete information in hypercubes[J].Journal of Systems Science and Systems Engineering,2012,21(4):422-442. |
| Click to display the text | |
| [7] | Yue Z L. A group decision making approach based on aggregating interval data into interval-valued intuitionistic fuzzy information[J].Applied Mathematical Modelling,2014,38(2):683-698. |
| Click to display the text | |
| [8] | Cerný M, Hladík M.The complexity of computation and approximation of the t-ratio over one-dimensional interval data[J].Computational Statistics and Data Analysis,2014,80:26-43. |
| Click to display the text | |
| [9] | Yang X J, Yan L L,Peng H,et al.Encoding words into cloud models from interval-valued data via fuzzy statistics and membership function fitting[J].Knowledge-Based Systems,2014,55:114-124. |
| Click to display the text | |
| [10] | 郭均鹏,陈颖, 李汶华.一般分布区间型符号数据的K均值聚类方法[J].管理科学学报,2013,16(3):21-28. Guo J P,Chen Y,Li W H.K-means clustering of generally distributed interval symbolic data[J].Journal of Management Sciences in China,2013,16(3):21-28(in Chinese). |
| Cited By in Cnki (5) | |
| [11] | 高飒. 一般分布区间型符号数据的聚类分析方法研究[D].天津:天津大学,2009. Gao S.The clustering analysis of generally distributed interval symbolic data[D].Tianjin:Tianjin University,2009(in Chinese). |
| Cited By in Cnki (6) | |
| [12] | Silverman B W. Density estimation for statistics and data analysis[M].London:Chapman and Hall,1986:34-48. |
| [13] | Fan J Q, Yao Q W.Nonlinear time series: nonparametric and parametric methods[M].New York:Springer Verlag,2003:193-212. |
| [14] | Marhuenda Y, Morales D,Pardo M C.Power results of tests for the uniform distribution,I-2005-09[R].Spain:Miguel Hernandez University of Elche,2005. |
| [15] | Kolmogorov A N. Sulla determinazione empirica di una legge di distribuzione[J].G Inst Ital Att,1933,4:83-91. |
| [16] | Sinclair C D, Spurr B D.Approximations to the distribution function of the anderson:darling test statistic[J].Journal of the American Statistical Association,1988,83(404):1190-1191. |
| Click to display the text | |
| [17] | Conover W J. Practical nonparametric statistics[M].New York:Wiley,1999:63-70. |
| [18] | Zhang J. Powerful goodness-of-fit tests based on the likelihood ratio[J].Journal of the Royal Statistical Society,Series B(Statistical Methodology),2002,64(2):281-294. |
| Click to display the text |