在图像处理与模式识别中,矩及矩的方程已被证明是一种非常实用的工具[1,2,3].在所有不同种类的矩中,应用最为广泛的是几何矩.几何矩及其不变矩最早在1962年由Hu[4]提出.但几何矩不是正交矩,这也导致当用几何矩描述图像时产生信息冗余,而且不能由几何矩进行图像重构;另外,几何矩是定义在连续空间上的,在数字图像上计算时会不可避免地引入近似而导致离散误差.为了解决以上第1个问题,Teague提出了正交的Legendre矩与Zernike矩[5].同时,复数矩[6]以及Gaussian-Hermite(GH)矩[7]也相继被提出.针对第2个问题,一些离散形式的正交矩也相继被提出.Mukundan等基于Tchebichef多项式提出了离散的Tchebichef矩[8],Yap等提出了离散正交的Krawtchouk矩[9],以及Zhu等提出了离散的Racah矩[10]和Dual Hahn矩[11].离散正交矩在计算的时候不需要进行近似也没有信息冗余,因此具有一定的优势.在这期间,也有一些其他形式的矩被提出并应用[12],甚至推广到三维空间中[13].自从Hu基于代数的方法提出了著名的7个几何不变矩之后,关于矩的不变矩成了研究的热点,并被广泛应用到图像处理与模式识别中.不变矩包括位移不变、旋转不变、尺度不变和仿射不变等.在图像处理领域,旋转不变的性质最为重要.有很多研究集中在几何矩的不变矩,其中贡献最大的是Flusser[14],他通过复数矩,推导几何矩的旋转不变矩的独立完备集,对几何矩的尺度不变矩也做了一定的研究[15].Zernike矩的旋转不变矩很容易就可以得到,因为它是定义在极坐标下的矩.Chong等给出了推导Zernike矩的位移不变矩的方法[16],还推导了Legendre矩的位移与尺度不变矩[17].也有一些研究集中在离散正交矩的不变矩的推导上,例如,Zhu等推导了离散的Tchebichef矩的位移与尺度不变矩[18].
虽然GH矩是定义在连续空间上,比起离散的正交矩,在图像处理中,GH矩依旧有一些优势.GH矩基函数的过零点的分布就是一个很好的例证.GH矩基函数的过零点分布比其他矩更加均匀,例如离散的Tchebichef矩,这也就说明GH矩具有更强的图像特征表述能力[19].另外,从计算角度讲,Tchebichef矩等基函数中存在阶乘的运算,使得它们计算非常耗时,而GH矩的计算相对简单许多.因此,对GH矩的研究具有实际应用意义.Yang等在文献[19]中尝试推导了GH矩的旋转不变矩,只说明几何矩的旋转不变矩形式也适合不带归一系数的GH矩.但他们并没有考虑到不变矩的独立性与完备性,而且去掉归一系数的做法有可能使矩的计算出现溢出.Refregier在文献[20]中定义极坐标形式下的Hermite多项式以及“Shapelet”,并用于星云图像分析中,但没有研究其旋转不变的性质.事实上,“Shapelet”与Shen提出的GH矩[7]是完全一样的,只是叫法与应用领域不同.本文从文献[14，19-20]得到启发,重点研究了GH矩的性质,侧重旋转不变矩的独立性与完备性,把GH矩推广到极坐标下,定义极坐标形式的GH矩,并通过极坐标下的形式推导了GH矩的旋转不变矩,给出推导所有GH矩旋转不变矩的独立完备集的方法.
1 GH矩 1.1 GH矩基函数
首先定义GH多项式:
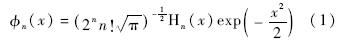
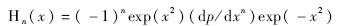
引入尺度因子σ,一维GH矩的基函数定义为
不难证明,上式仍然满足正交归一性:
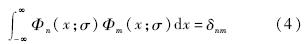
由一维推广到二维,在笛卡儿坐标系下,二维的GH矩的基函数为
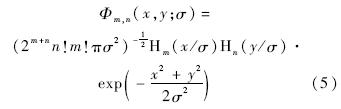
图 1给出了GH矩前5阶矩的基函数的灰度图像.
 |
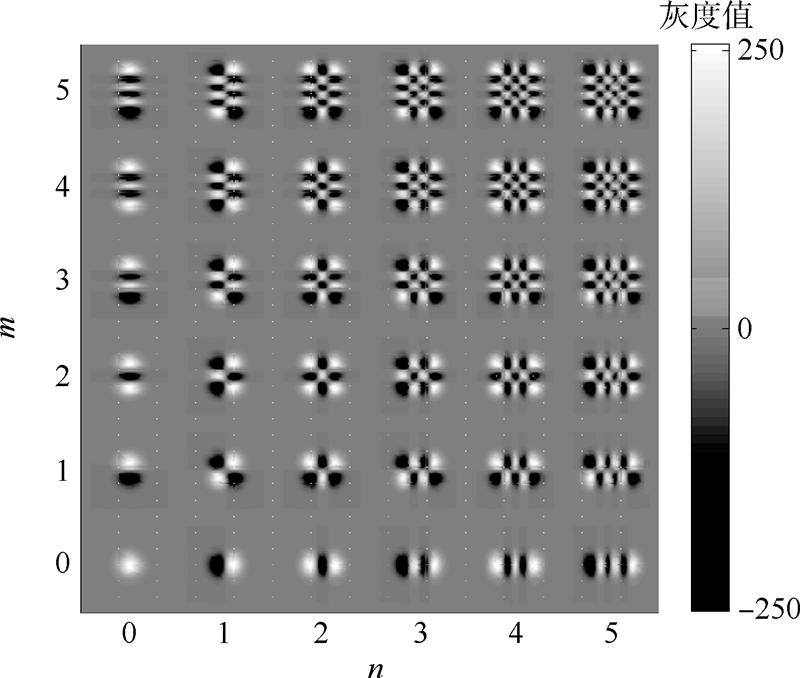| 图 1 GH矩的前5阶矩的基函数Fig. 1 Basic functions under order 5 of GH moments |
给定图像函数f(x,y),并由式(1)的基函数,GH矩定义为
由定义可知,事实上,GH矩是由图 1中GH矩的基函数与图像进行卷积运算得到.
1.3 用升降算符计算GH矩的基
事实上,GH矩的基函数是量子力学中量子谐振子的本征函数,而阶数m,n即为本征函数对应的本征值.具体阶数的本征函数可以通过初始本征函数与算符的迭代作用计算得到.因此,GH矩的基函数可以通过构建升降算符来计算.
量子谐振子的降算符和升算符分别为
=1.利用升算符,给定初始函数,以及以下的递推关系,可以计算得到一系列本征函数:
对于二维的情况,同样可以用升算符推导:
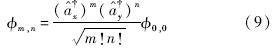
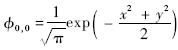.所以,GH矩的基Φm,n(x,y;σ),可以通过构建以下升降算符来计算:
递推公式为
相应地,(0,0)阶基函数为
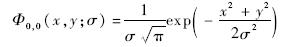
因此,所有的GH矩的基函数都可以通过(0,0)阶基函数与升算符计算得到.
1.4 离散形式
GH矩是定义在连续区间(-∞,∞)上的.GH矩中存在尺度因子σ,在计算矩之前应先设定好大小.对于不同大小的图像,为了更方便设定尺度因子,应把图像坐标转换到一个固定的区间里.因此,这里根据通常的使用习惯选择区间[-1,1],即对于一个定义在区间[0≤i,j≤K-1]上的数据图像I(i,j),图像坐标首先通过下面的式子进行转换:
那么,定义在图像I(i,j)上p+q阶的GH矩就可以通过式(13)计算得到:
2 PGH矩 2.1 PGH矩的基函数
为了构造极坐标下的GH矩(PGH,Polar-Gaussian-Hermite)的基函数,先定义左右降算符如下:
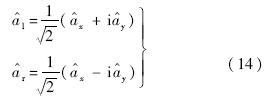
对应的升算符为
它们的对易关系是
.
同样,利用左右升算符,给定初始函数,以及以下递推关系,可以计算得到一系列本征函数:
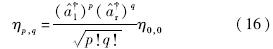
把左右升算符转换成极坐标形式,由式(7)代入式(14)和式(15),并由x=rcosθ,y=rsinθ可以得到:
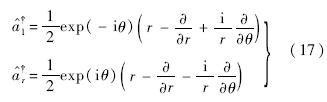
那么给定初始函数
,由式(16)和式(17)可以得到:
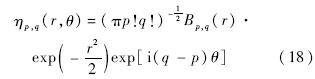
引入尺度因子σ,左右升算符为
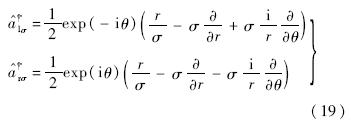
给定初始函数
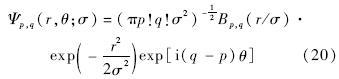
图 2给出了PGH矩的前5阶矩的基函数的灰度图像.
 |
| 图 2 PGH矩前5阶矩基函数Fig. 2 Basic functions under order 5 of PGH moments |
给定图像函数f(r,θ),并由式(20)的基函数,可以定义PGH矩为
2.3 GH矩与PGH矩的关系
前面已经给出了GH矩和PGH矩的定义,以及它们的基函数，同时也给出了各自用升降算符来计算所有基函数的方法.
由直角坐标与极坐标的关系可以知道,GHM的基函数的初始函数Φ0,0(x,y;σ)=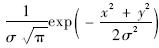
和PGHM的基函数的初始函数
是完全一样的.也就是说,GHM和PGHM是由同一个初始函数,但由不同的升算符不停地作用而构成的不同的函数群.
那么由递推关系式(11)与式(16),并联立两组升算符之间的关系,二项式展开,可以得到GH矩和PGH矩一一对应的相互转换公式:
3 GH矩的旋转不变矩
由图 2a可以看出,当p=q,即对角线上的实数部分的基函数是旋转不变的.已经知道,GH矩与PGH矩是一一对应的,所以,由转换公式(24)就可以推导GH矩的旋转不变矩的形式.但是这样得到的GH矩的旋转不变矩并不是独立的,更重要的,仅仅只是由p=q的实数部分推导得到的GH矩的旋转不变矩不是完备集.本文的目的是推导GH矩的旋转不变矩的独立完备集.
3.1 旋转不变的推导
为了推导GH矩的旋转不变矩,已经把GH矩推导到极坐标空间中,即PGH矩.而由于PGH矩是定义在极坐标空间中,具有以下重要的旋转性质.
定理1 假设图像f经过旋转一个角度α后为f′,f′(r,θ)=f(r,θ+α),f′的PGH矩表示为P′p,q,那么
证明是显而易见的.
上式表明,PGH矩的模|Pp,q|是旋转不变的,而象角平移了(q-p)α个单位.
如果只是用PGH矩的模来构造一组旋转不变矩,并不能构成一组完备集,遗失了很多有用的不变矩.下面的理论将构建一组旋转不变矩的独立的完备集.
定理2 n≥1,ki,pi,qi为非负整数,如果:
证明 让图像旋转一个角度α:
已知如何推导旋转不变矩,定理3将解决怎样推导给定阶数的旋转不变矩的独立完备集.
定理3 考虑r≥2阶以上的PGH矩,一组旋转不变矩集构造为
以上推导了GH矩的旋转不变矩的独立完备集.现在给出其详细证明.
证明 集合B的完备性.使I为任意旋转不变矩：
归纳Pp0,q0与Pq0,p0可以得到
由于I是旋转不变矩,所以有
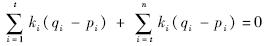
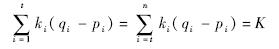
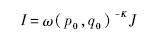
这就证明了任意的不变矩I都可以由J推导出,从而证明了集合B的完备性.
集合B的独立性.假设B是非独立的,即存在ω(p,q)∈B依赖于B-{ω(p,q)},那么当p=p0和q=q0时,也是成立的.也就是,在B-{ω(p,q)}中存在ω(p1,q1),…,ω(pn,qn)与ω(u1,v1),…,ω(un,vn)使得
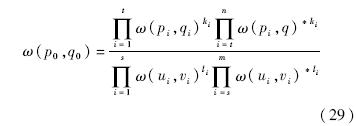
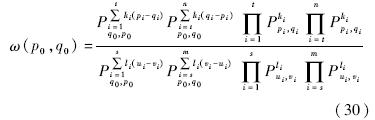
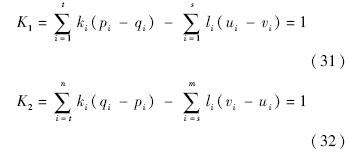
由于上式右边等于1,并且不同的矩之间各自独立,所以下列等式对所有i都成立:t=s,n=m,pi=ui,qi=vi,ki=li
那么代入式(31)和式(32)得到K1=0和K2=0,矛盾.因此证明了独立性.证毕
3.2 GHM旋转不变矩的独立完备集
根据定理3,给定矩的阶数,就可以得到一组独立完备的旋转不变矩集.以下给出前6阶矩的旋转不变矩集.
2,3阶矩:
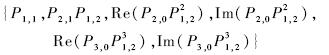
4阶矩:
5阶矩:
6阶矩:
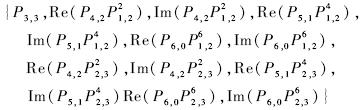
根据以上给出的形式,以及PGH矩展开成GH矩公式(24),可以得到GHM的旋转不变矩形式.这里给出2阶矩、3阶矩的6个不变矩形式如下:
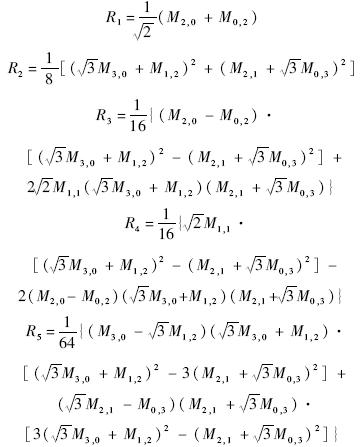
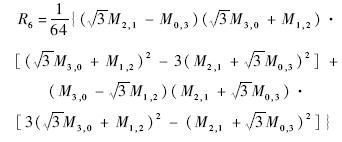
本实验是为了验证所提出的不变矩的正确性与数字稳健性.图 3a是原始医学图像,分辨率为256像素×256像素,7个不同旋转角度的图像是由电脑严格生成,分别为图 3b~图 3h.
 |
| 图 3 医学灰度图像及其旋转版本Fig. 3 Medical image and its rotational versions |
分别计算8幅图像的旋转不变矩.尺度因子设为0.2,尺度因子的大小只用于计算需求,并不会影响旋转不变性.实验数据记录在表 1中.
| 角度/(°) | ψ1 | ψ2 | ψ3 | ψ4 | ψ5 | ψ6 | ψ7 | ψ8 | ψ9 |
| 0 | 13.3810 | 3.1951 | 4.0437 | 1.1853 | 4.6365 | 3.9185 | 14.0222 | 1.7622 | -0.3699 |
| 20 | 13.3818 | 3.1947 | 4.0416 | 1.1862 | 4.6340 | 3.9162 | 14.0179 | 1.7641 | -0.3687 |
| 70 | 13.3816 | 3.1968 | 4.0453 | 1.1890 | 4.6345 | 3.9282 | 14.0184 | 1.7659 | -0.3683 |
| 110 | 13.3818 | 3.1947 | 4.0416 | 1.1862 | 4.6340 | 3.9162 | 14.0179 | 1.7641 | -0.3687 |
| 170 | 13.3825 | 3.1940 | 4.0415 | 1.1896 | 4.6287 | 3.9259 | 14.0180 | 1.7630 | -0.3696 |
| 200 | 13.3818 | 3.1947 | 4.0416 | 1.1862 | 4.6340 | 3.9162 | 14.0179 | 1.7641 | -0.3687 |
| 230 | 13.3821 | 3.1955 | 4.0412 | 1.1903 | 4.6317 | 3.9329 | 14.0193 | 1.7642 | -0.3672 |
| 310 | 13.3812 | 3.1979 | 4.0462 | 1.1843 | 4.6390 | 3.9185 | 14.0187 | 1.7660 | -0.3728 |
| 偏差/% | 0.0026 | 0.0303 | 0.0410 | 0.1560 | 0.0423 | 0.1418 | 0.0070 | 0.0492 | 0.3120 |
| 角度/(°) | ψ10 | ψ11 | ψ12 | ψ13 | ψ14 | ψ15 | ψ16 | ψ17 | ψ18 |
| 0 | -1.7296 | -1.4225 | 7.8066 | 4.8990 | -0.9706 | 1.3113 | 1.2079 | -26.2475 | -42.1389 |
| 20 | -1.7265 | -1.4251 | 7.8041 | 4.8980 | -0.9704 | 1.3112 | 1.2028 | -26.2279 | -42.0656 |
| 70 | -1.7279 | -1.4292 | 7.8020 | 4.8990 | -0.9697 | 1.3069 | 1.2054 | -26.2292 | -42.1714 |
| 110 | -1.7265 | -1.4251 | 7.8041 | 4.8980 | -0.9704 | 1.3112 | 1.2028 | -26.2279 | -42.0656 |
| 170 | -1.7261 | -1.4266 | 7.8003 | 4.8965 | -0.9690 | 1.3110 | 1.2068 | -26.1806 | -42.1137 |
| 200 | -1.7265 | -1.4251 | 7.8041 | 4.8980 | -0.9704 | 1.3112 | 1.2028 | -26.2279 | -42.0656 |
| 230 | -1.7235 | -1.4314 | 7.8068 | 4.9001 | -0.9680 | 1.3102 | 1.2039 | -26.1296 | -42.1269 |
| 310 | -1.7275 | -1.4221 | 7.8089 | 4.9019 | -0.9714 | 1.3115 | 1.2096 | -26.2772 | -42.2547 |
| 偏差/% | 0.0688 | 0.1673 | 0.0274 | 0.0243 | 0.0828 | 0.0774 | 0.1801 | 0.1208 | 0.1131 |
由数据可以看出,这8幅图像所计算得到的不变矩的基本值保持不变,不因角度的变化而变化.但同时,它们并不是绝对不变的,这是因为在生成旋转图像的时候不可避免地进行插值运算,图像的灰度方程发生了细微的改变,导致最终矩的计算结果不完全相等，但是波动是在一定的范围内.用不变矩的平均偏差百分比
×100%来评估计算结果的数字稳健性,ξ和|μ|分别代表不变矩的标准差和平均值.越小的平均偏差百分比代表更好的数字稳健性,相反,值越大代表越不稳定.对图 1中的所有图像所计算得到的不变矩,所有的平均偏差百分比值都小于0.2%.这证明了所提出的GH矩的不变矩的正确性,同时其具有良好的数字稳健性.
本文介绍了GH矩PGH矩,并给出了用升降算符计算GH矩与PGH矩的方法.利用GH矩与PGH矩的一一对应关系,详细推导了GH矩的旋转不变矩,并给出GH矩的旋转不变矩的独立完备集.从实验结果可以看出,所提出的旋转不变矩具有良好的数字稳健性,GH矩的旋转不变矩的推导方法具有一般性,在推导其他形式的矩的旋转不变矩时可以借鉴.但本文并未详细研究GH矩的旋转不变矩的应用,例如应用于图像配准与检索,下一步将着手这一方面的研究.
| [1] | Xiao B,Ma J F,Cui J T.Combined blur, translation,scale and rotation invariant image recognition by Radon and pseudo-Fourier-Mellin transforms[J].Pattern Recognition,2012,45(1):314-321 |
| Click to display the text | |
| [2] | Papakostas G A,Koulouriotis D E,Karakasis E G,et al.Moment-based local binary patterns:a novel descriptor for invariant pattern recognition applications[J].Neurocomputing,2013,99:358-371 |
| Click to display the text | |
| [3] | Yang J,Xie S,Yoon S,et al.Fingerprint matching based on extreme learning machine [J].Neural Computing and Applications, 2013,22(3/4):435-445 |
| Click to display the text | |
| [4] | Hu M K.Visual pattern recognition by moment invariants[J].IRE Transactions on Information Theory,1962,8(2):179-187 |
| Click to display the text | |
| [5] | Teague M R.Image analysis via the general theory of moments[J].Optical Society of America,1980,70(8):920-930 |
| Click to display the text | |
| [6] | Abu-Mostafa Y S,Psaltis D.Image normalization by complex moments[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1985,PAMI-7(1):46-55 |
| [7] | Shen J.Orthogonal Gaussian-Hermite moments for image characterization[C]//Proceedings of SPIE-The International Society for Optical Engineering.Bellingham WA:SPIE,1997:224-233 |
| Click to display the text | |
| [8] | Mukundan R,Ong S,Lee P A.Image analysis by Tchebichef moments[J].IEEE Transactions on Image Processing,2001,10(9):1357-1364 |
| Click to display the text | |
| [9] | Yap P T,Paramesran R,Ong S H.Image analysis by Krawtchouk moments[J].IEEE Transactions on Image Processing,2003,12(11):1367-1377 |
| Click to display the text | |
| [10] | Zhu H,Shu H,Liang J,et al.Image analysis by discrete orthogonal Racah moments[J].Signal Processing,2007,87(4):687-708 |
| Click to display the text | |
| [11] | Zhu H Q,Shu H Z,Zhou J,et al.Image analysis by discrete orthogonal dual Hahn moments[J].Pattern Recognition Letters,2007,28(13):1688-1704 |
| Click to display the text | |
| [12] | Zhang C X,Xi P,Dai M.Gaussian-geometric moments and its application in feature matching[J].Advanced Materials Research,2013,718-720:2113-2119 |
| Click to display the text | |
| [13] | Mangin J F,Poupon F,Rivière D,et al.3D moment invariant based morphometry[J].Lecture Notes in Computer Science,2003,2879(Part2):505-512 |
| Click to display the text | |
| [14] | Flusser J.On the independence of rotation moment invariants[J].Pattern Recognition,2000,33(9):1405-1410 |
| Click to display the text | |
| [15] | Suk T,Flusser J.Affine moment invariants generated by graph method[J].Pattern Recognition,2011,44(9):2047-2056 |
| Click to display the text | |
| [16] | Chong C W,Raveendran P,Mukundan R.Translation invariants of Zernike moments[J].Pattern Recognition,2003,36(8):1765-1773 |
| Click to display the text | |
| [17] | Chong C W,Raveendran P,Mukundan R.Translation and scale invariants of Legendre moments[J].Pattern Recognition,2004,37(1):119-129 |
| Click to display the text | |
| [18] | Zhu H,Shu H,Xia T,et al.Translation and scale invariants of Tchebichef moments[J].Pattern Recognition,2007,40(9):2530-2542 |
| Click to display the text | |
| [19] | Yang B,Li G,Zhang H,et al.Rotation and translation invariants of Gaussian-Hermite moments[J].Pattern Recognition Letters,2011,32(9):1283-1298 |
| Click to display the text | |
| [20] | Refregier A.Shapelets-I:a method for image analysis[J].Monthly Notices of the Royal Astronomical Society,2003,338(1):35-47 |
| Click to display the text |