过冷水滴(温度低于0℃但保持液态)撞击低温固体表面导致的积冰是自然界和工程活动中的一种复杂现象,冰层在建筑结构、飞机、船舶和制冷设备表面的累积已经困扰了工程师们很多年.其中飞机、高速列车和船舶等交通载运工具迎风面的积冰属于过冷水滴撞击高速运动物体表面的结冰现象;建筑结构、电力系统高架塔和传输线表面的积冰属于过冷水滴在重力或风力作用下坠落静止物体表面的结冰现象.影响积冰的主要因素有:空气中过冷水含量、水滴平均有效直径、空气流速、积冰部位的曲率半径、结冰时间和环境温度等.根据结冰表面是否存在水膜,积冰可以分为霜冰、明冰以及二者的混合.对过冷水滴积冰现象的数值模拟一般分为3个步骤:运载水滴的空气流场计算、水滴运动轨迹的计算以及积冰计算,这3种过程被解耦为独立步骤依次执行.采用准定常方法处理积冰的非定常问题,在上述步骤组成的计算流程中空气流场和水滴分布都被认为是定常的,当冰形发生显著改变时通过更新壁面边界位置来重复计算流程,直到预计的积冰时间.
霜冰与明冰计算的主要区别在于计算流程的第3步,在由水滴运动轨迹构建表面水滴收集系数后,明冰计算必须模拟水膜的流动而霜冰计算则不需要考虑.传统的计算水膜溢流的积冰模型是由Messinger[1]提出的一维质量、能量守恒方程,这种经典的模型和处理方法也被目前很多飞行器积冰软件所采用,如NASA Glenn研究中心开发的Lewice[2].Messinger模型对结冰表面的水膜流动做了最简化的处理,未冻结的水全部流入下风向的单元内,只适合计算空气切应力占支配作用的高速运动物体积冰,在静止物体积冰的低速环境下,空气动力不再是主要驱动力,因此不能采用水膜沿气流方向流动的简单假设.Messinger模型也没有考虑已经形成的冰层对积冰过程的影响,对溢流水流动趋势的预测偏大;在温度相对较高,明冰比例较大的情况下,这种效应将更为明显.此外,Messinger模型假设明冰条件下的水膜流通量是定常的,对于外部流场和壁面形状都随时间变化的积冰过程而言,非定常的水膜流通量显然更接近物理真实情形.Myers等人[3,4]基于流体力学中的润滑理论提出了多种外力驱动的水膜流动模型,同时也给出了包含冰层内部传热效应的积冰模型.Messinger模型中的两个代数守恒方程被两个守恒形式的偏微分方程所代替;积冰的实际物理过程在模型中得到了更为清晰的解释,水膜的流动方向由作用于水膜的各种外力综合决定.Myers的水膜-冰层模型是与Messinger模型完全不同的第2代积冰模型,这种模型被应用在最新的积冰软件ICECREMO中[5].Verdin等人[6,7]采用结合水膜-冰层模型的准定常多步法计算了翼型、圆柱体等一些简单二维部件截面的冰形,得到了与实验较为一致的结果,从而验证了模型的有效性.但是,这些文献对具体的数值求解方法的表述并不明确,而且模拟对象主要是翼型等高速运动物体,对传输线等低速环境下的积冰模拟较为少见.
针对传统Messinger模型存在的主要缺陷,基于润滑近似,本文将文献[3]中水膜-冰层模型在二维笛卡儿坐标系下的形式推广到正交曲线坐标系,提出适用于任意形状截面积冰计算的水膜流动方程和积冰方程.采用一种隐式有限差分格式数值求解控制水膜流动的偏微分方程,采用典型显式格式求解积冰方程;与全显式的离散格式比较,这种离散方法具有更好的稳定性和鲁棒性.选取两类具有代表性的积冰环境验证数值方法的有效性:一种是Messinger模型有效的高速积冰条件;另一种是Messinger模型难以预测的低速积冰条件.这两种积冰条件的主要区别在于空气自由流速度的差异.对于高速积冰,采用NACA0012翼型作为结冰几何体;对于低速积冰,采用简单的圆柱剖面作为结冰几何体.两种几何体分别代表高速环境下的机翼积冰以及低速环境下的传输线积冰.冰形的计算结果与文献中给出的数值模拟结果以及冰风洞实验结果进行对比.
1 数学模型 1.1 润滑理论对表面水膜流动的近似处理
与空气流动解耦后,连续分布的水膜流动属于典型的自由表面流,采用润滑理论的假设描述薄膜流,通过对Navier-Stokes(N-S)方程进行无量纲化可以略去充分小项,使方程组形式明显简化,最终得到只含一个标量的偏微分方程.润滑理论的基本假设为[8]:
1) 水膜连续分布,满足连续介质的条件.
2) 水膜的厚度H相对于横向尺度L的比率(长宽比)ε(H/L)以及消减雷诺数ε2Re都是可以略去的充分小量(Re为水膜流动的雷诺数).
润滑假设并不考虑水滴在形成连续水膜之前的流动状态,也不考虑水滴的碰撞对水膜流动的影响,因此一般适用于空气中的液态水含量(LWC,Liquid Water Content)较小(0.1~5 g/m3),过冷水滴的有效直径(MVD,Median Volumetric Diameter)小于50 μm的积冰条件.
经过量纲分析,对于二维斜平面,以沿斜面向上方向为x轴正向,斜面法向为z轴正向建立坐标系,笛卡儿坐标下的N-S方程可以简化为[3]
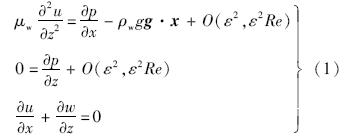
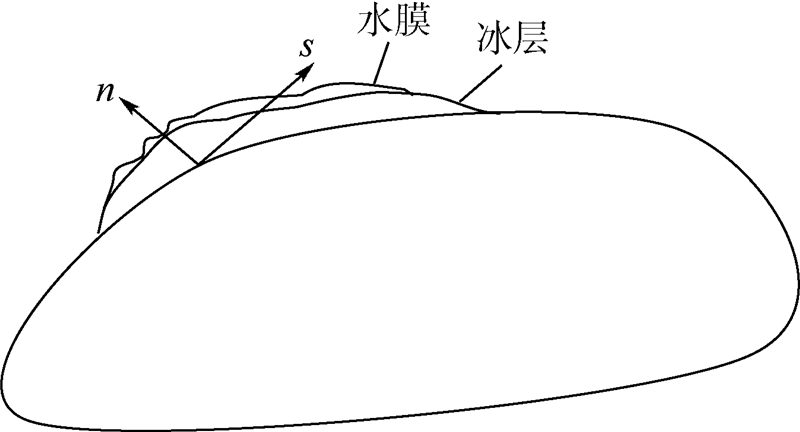 |
| 图 1 二维截面的正交曲线坐标系图示Fig. 1 Diagram of orthogonal curvilinear coordinate system on two-dimensional section |
正交坐标系下的简化N-S方程为[4]
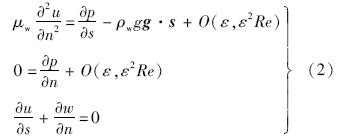

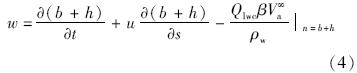
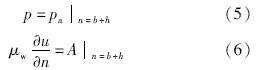
沿截面法向n对方程组(2)积分,积分范围为b~b+h,将运动边界条件式(4)代入积分结果,根据式(3)~式(6),最终得到二维截面表面水膜流动的控制方程:
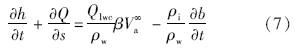
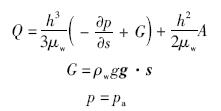
1.2 积冰方程
描述水膜流动的控制方程(7)等号右侧第2项为未知项,表示水膜底层的积冰率,因此方程不封闭.由于积冰过程与能量方程相关,可以将润滑近似推广到水膜的能量方程:
1) 水膜的长宽比ε(H/L)是一个充分小量.
2) 水膜的Peclet数也是一个充分小量,Peclet数代表对流项与热传导项的量纲之比,表明水膜能量方程中起支配作用的是热传导.
在上述假设下经量纲分析,水膜的能量方程可以简化为
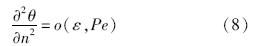
对水膜能量方程采用的边界条件是水膜与冰层界面处的温度恒等于冰点温度Tf,水膜上层自由表面的热流量由空气的壁面传热量、水滴撞击带给水膜的热量以及水膜蒸发所带走的潜热之和Q决定:

冰层内部的传热情况可以采用热传导方程来描述,对冰层的热传导方程采用如下的假设:
1) 冰层的厚度与冰层的横向尺度之比ε(B/L)是一个充分小量;
2) 忽略初始时刻冰晶和水膜的形成过程中复杂的非稳态传热和瞬时成核现象.
经量纲分析,同样可得到简化的冰层热传导方程:
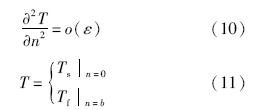
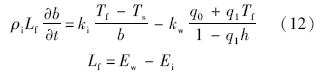
方程(12)适用于结冰表面存在水膜的明冰条件,霜冰条件下的积冰方程只由壁面水滴收集系数决定,可以表示为

方程(13)可以作为对模型的一个简单扩充加入计算过程,在积冰随时间的推进过程中由模型来判断水膜产生的时刻和位置.
1.3 水膜-空气界面的能量传递
水膜能量方程的边界条件式(9)包含水膜-空气界面处传递的总热流量Q,Q的具体形式为
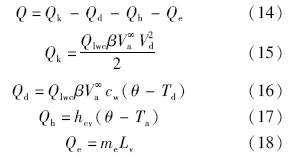
根据总热流量Q的具体形式,积冰方程(12)的自由表面传热参数q0,q1分别为
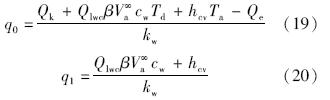
基于Messinger模型的自由表面总热流量通常还要加上绝热升温项Qa,这一项适用于边界层积分法对传热现象的描述,绝热升温项是空气速度由边界层外缘的ue绝热减小至壁面处的0值所释放的热量;由于对流效应会带走一部分热量,需要将绝热升温量乘以一个复温因子R(通常小于1)以获得壁面上真实的升温效应:

2 数值求解方法 2.1 水膜流动方程的数值求解方法
方程(7)是一个典型的一维守恒律方程,关于守恒律已经有很多相关的数值解法,常用的显式有限差分格式为
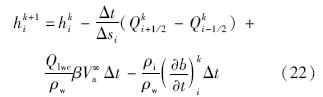
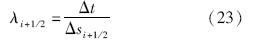
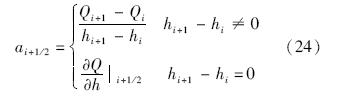
当CFL数大于1时,显式格式不再满足Von-Neumann线性稳定性,这要求时间间隔Δt需要取一个充分小值,如果截面型线某点处的波速a过大(这在角状冰引发的分离流时常出现),满足CFL条件的Δt就要非常小,这造成计算时间的显著增加.
为提高数值格式的稳定性和计算效率,采用一种半隐式格式代替显式格式:
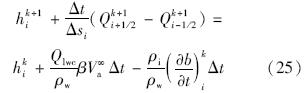
除了积冰项采用上一时间步的显式形式外,其余格式都是隐式的.界面处流通量Qi+1/2k+1采用一阶迎风格式计算:
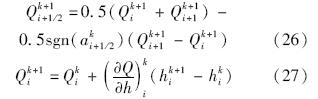
经式(27)线性化后最终得到三对角线性方程组,可以采用简洁的追赶法(TDMA,Tridiagonal Matrix Algorithm)数值求解.这种格式在时间和空间上都是一阶精度,对于不要求高精度水膜流动数值解的积冰计算是足够的.
2.2 积冰方程的数值求解方法
采用典型显式差分格式离散方程(12):
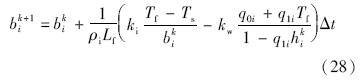
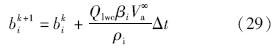
为克服数值奇性,在实际的时间推进中以纳米量级的水膜厚度hp和微米量级的冰层厚度bp作为初始条件,计算流程如下.
1) 首先假设型线表面全部为明冰,利用式(25)计算出新时刻的水膜厚度.
2) 当h>hp时表明该单元的明冰假设合理,用式(28)计算新时刻的冰层厚度;当h<hp时表明该单元属于霜冰,重新令h=hp并采用式(29)计算霜冰厚度.
但为了确保守恒性,式(29)应该做以下改变:
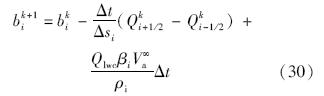
相对式(29),式(30)加入了与霜冰区单元相邻的明冰区单元的溢流水流通量,这种现象在明冰条件下十分常见,在没有过冷水滴撞击的区域会形成积冰正是由于明冰区水膜的溢流效应.
由于积冰方程是建立在由型线和法向线组成的正交曲线坐标系中的,冰形的增长自然地采用法向外延的几何增长算法,即求得冰层厚度b后,作为型线表面各单元的法向延伸长度计算新坐标值:
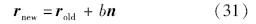
3 模型输入参数的计算 3.1 空气压强、壁面切应力和表面传热系数的计算
水膜-冰层模型需要空气在壁面处的压强和切应力作为模型输入参数,这两个参数通过计算流体力学(CFD,Comprtational Fluid Dynamics)方法求解空气绕流流场获得.
作为水膜-冰层模型的热动力输入参数,表面的对流换热系数是由空气的能量方程决定的.Lewice,ONERA[10]等第1代积冰软件都是采用一维边界层积分法对翼型壁面换热系数进行计算,当翼型前缘形成角状冰后,由于分离的发生边界层方法就显得不太有效,这也是Lewice等软件无法对大尺度角状冰进行有效预测的原因之一.由于典型高速积冰条件下的自由流马赫数(0.1~0.8)都大于决定空气可压缩与不可压缩性质的临界马赫数,本文采用基于Spalart-Allmaras(S-A)湍流模型[11]的可压缩N-S方程对表面换热系数进行计算,尽管S-A湍流模型对极端逆压梯度下分离流的模拟也不完全精确,但对角状冰绕流的适应性应该优于基于雷诺比拟的热边界层方法.
壁面粗糙度对壁面的对流换热有显著影响,由于积冰表面的粗糙度形成机理十分复杂,在数值模拟中难以进行有效预测,目前多采用基于经验公式的等效沙粒粗糙度进行简化计算.本文采用Shin等人提出的粗糙度经验公式[12],是Shin等人为提高Lewice软件冰形计算的准确性,根据冰风洞中的冰形实验结果拟合得出的;由于Lewice软件采用边界层积分法计算表面换热系数,这个经验公式主要适用于边界层方法.目前很难在各类文献中找到针对S-A湍流模型拟合的粗糙度经验公式,因此本文继续采用Shin的经验公式计算粗糙度.Shin公式也是第2代积冰软件FENSAP-ICE[13]计算粗糙度的依据,在FENSAP模块中作者同样采用了附加粗糙度项的S-A湍流模型计算表面换热系数.
3.2 水滴壁面收集系数和撞击速度的计算
与水滴撞击特性相关的两个输入参数,水滴壁面收集系数和撞击速度是由水滴轨迹决定的.本文采用欧拉两相流法求解空气-水滴两相流场.由于积冰条件下液态水滴含量极小(相体积率在10-6量级),水滴对空气流场的反作用可以忽略,因此对空气-水滴两相流场的求解简化为对空气绕流流场和水滴轨迹分别求解.壁面附近水滴撞击与水膜流动解耦处理,对水滴的壁面边界采用单向过滤的特殊边界条件[14].通过求解水滴欧拉方程计算近壁面首层网格的水滴相体积率和流动速度得到水滴壁面收集系数和撞击速度. 4 算例验证及分析 4.1 翼型积冰
在典型的高速积冰条件下,空气自由流速度一般在50~200 m/s的范围内;如果表面积冰类型为明冰,那么驱动水膜流动的主要外力是空气对壁面的切应力,Messinger模型中水膜沿气流方向流动的假设是成立的.本文选取NACA0012翼型作为结冰几何体,以翼型型线为s轴,翼型表面法向为n轴建立正交曲线坐标系.积冰条件如表 1所示,采用的是文献[15]中提供的在低温和相对高温环境下的两种典型算例,表 1中给出了算例在文献[15]中对应的运行编号.
| 编号 | 弦长/m | 自由流速率/(m/s) | 静温/K | 攻角/(°) | Qlwc/(g/m3) | MVD/μm | 时间/min |
| r401 | 0.533 4 | 102.8 | 265.37 | 4 | 0.55 | 20 | 7 |
| 062791.002 | 0.533 4 | 58.1 | 269.19 | 4 | 1.3 | 20 | 8 |
为提高冰形计算的准确度,本文采用准定常多步法更新模型输入参数,即每隔一定时间间隔重新计算当前冰形的定常空气绕流流场和水滴流场,根据流场计算结果更新空气壁面切应力、静压、表面换热系数以及水滴收集系数和撞击速度.以r401算例为例,总的积冰时间为7 min,以1 min为时间间隔分7步进行时间推进.在每个时间间隔内求解式(7)和式(12)、式(13)组成的非定常方程组,因此准定常外部时间步内又存在内部时间步长.两个算例在初始阶段均采用Δt=1 ms作为内部时间步长,当数值推进不稳定时可以适当减小内部时间步长.冰层按照外部时间间隔的推进过程如图 2所示.
 |
| 图 2 算例r401的7×1 min多步推进过程Fig. 2 Example r401,multi-stepping advanced process of 7×1 min |
图 3a、图 3b为两个算例的最终冰形与文献[15]中给出的IRT冰风洞实验结果和Lewice软件数值计算结果之间的比较.以冰风洞的实验冰形为参照,水膜-冰层模型的计算结果可以较准确地预测出冰形在翼型上下翼面延伸的极限以及冰角的位置和形状.图 2a中最终冰形与Lewice计算的冰形位置相当,在翼型前缘端点附近的冰形略优于Lewice的计算结果.图 2b中水膜-冰层模型的预测冰形无论在上下限位置还是前缘附近都明显优于Lewice程序的计算结果,Lewice高估了水膜的流动趋势,这导致上下翼面冰层过厚而前缘附近冰层过薄.除了对水膜流动处理方式上的差异,Messinger模型与水膜-冰层模型最大的不同在于热动力模型部分;其中水膜-冰层模型考虑了冰层内部的热传导,而Messinger模型则完全忽略了此项,即Messinger模型忽略了方程(12)等号右侧的第1项.这种区别在算例r401代表的低温环境下并不显著,这是由于低温环境的积冰速率很快,方程(10)所描述的稳态热传导来不及完全建立,因此冰层热传导的影响并不大.但已经可以发现Messinger模型容易低估前缘点附近的积冰量,在一定程度上正是由于忽略了冰层传热的影响.在更温暖的环境温度下积冰速率相对缓慢,冰层内部的温度分布接近稳态分布,热传导效应的影响就十分明显了.因此在环境温度接近冰点的明冰条件下,采用包含冰层导热的传热模型更有助于得到准确的冰形.
 |
| 图 3 翼型积冰算例最终冰形的对比图Fig. 3 Comparison of final ice shapes on airfoil |
水膜-冰层模型在预测冰角形状的敏感性上表现出了良好的特性,由于水膜-冰层模型中的模型输入参数更丰富,并且考虑了已经存在的冰层对冰形增长的影响,基于水膜-冰层模型的冰形计算对多步法中模型输入参数的变化响应更大.即使只采用单步法计算最终冰形(不再更新模型输入参数),由于水膜-冰层模型包含有非定常时间推进,同样可以计入水膜溢流和累积冰层对冰形增长的影响,而单步法的Messinger模型中的冻结系数则是一个不随时间变化的常量.
4.2 传输线积冰
由于在高速积冰条件下空气切应力支配了水膜流动,翼型积冰并没有反映出水膜-冰层模型对水膜流动的处理与Messinger模型的差异.过冷细雨(小直径的冻雨)导致的电力系统传输线表面的积冰是在典型的低速积冰条件下发生的,由于降雨经常伴随着不同等级的风力,一般会将水平方向的空气流动因素考虑在内.根据风力等级的不同,低速积冰的空气自由流速度一般在1~10 m/s的范围内.本文选取代表传输线截面的圆柱截面作为结冰几何体,以圆在各点的切线为s方向,以圆的法线方向为n方向建立正交坐标系.具体的积冰条件如表 2所示.
| 编号 | 直径/m | 自由流速率/(m/s) | 静温/K | LWC/(g/m3) | MVD/μm | 时间/min |
| case4 | 0.034 9 | 10 | 268.15 | 1.8 | 26 | 30 |
| case5 | 0.019 05 | 5 | 268.15 | 1.8 | 33 | 30 |
表 2中算例编号与文献[16]提供的运行编号相同,自由流条件并没有考虑水滴的坠落速度,而是认为远场处水滴的速度与空气自由流速度相同.即使空气自由流速度在1~10 m/s的范围内,自由流雷诺数仍在103~104量级,对于圆柱绕流采用湍流模型仍然是必要的.但由于自由流速度远小于声速,利用S-A模型计算空气绕流流场和表面换热系数时可以采用不可压缩假设.建立圆柱表面粗糙度与积冰条件之间的关系十分困难,本文在计算对流换热系数时没有考虑粗糙度的影响.采用3步准定常时间推进更新模型输入参数和冰形,图 4给出了算例case5的具体推进过程,准定常时间间隔为10 min.
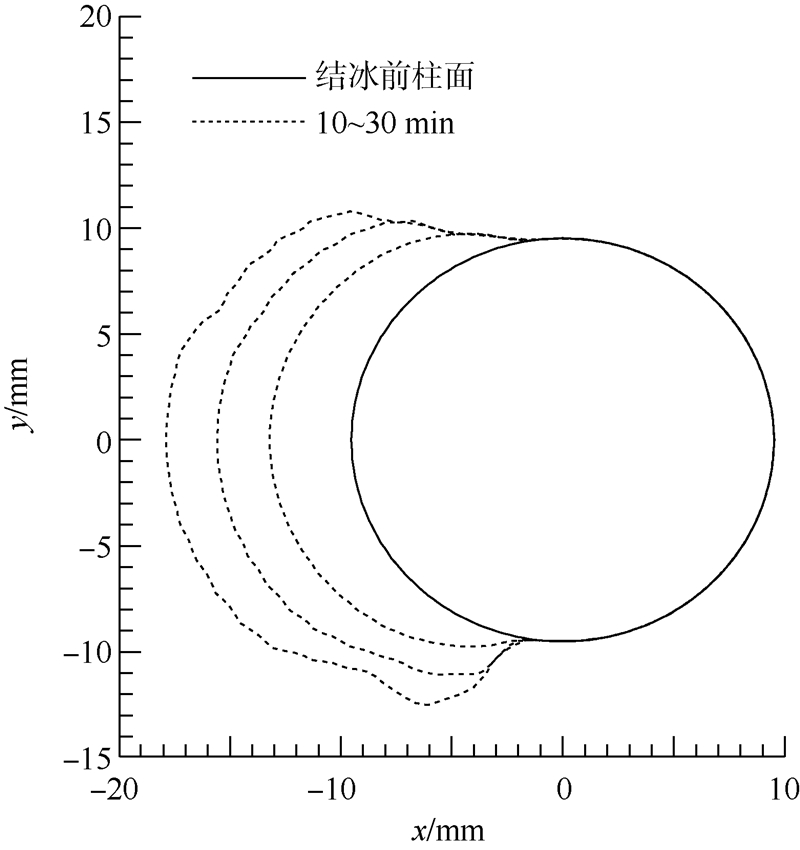 |
| 图 4 算例case5的3×10 min多步推进过程Fig. 4 Example of case5,multi-stepping advanced process of 3×10 min |
图 5a、图 5b是传输线表面的计算冰形与文献[16]给出的CAIRWT冰风洞实验结果以及数值模拟结果之间的比较.即使外部空气流场、水滴流场以至表面传热系数、水滴壁面收集系数都以水平轴为近似对称面,算例case4和case5的最终冰形在水平轴上下都呈现出明显的不对称性.与高速积冰条件相比,传输线积冰的最大特点是空气切应力对水膜的作用与重力的作用相当,无风环境下空气切应力甚至可以被忽略.在明冰条件下表面水膜不能简单地假设是从驻点开始向下风向流动,实际上驻点是通过空气流场寻找的,只考虑了空气对水膜的作用.Messinger模型把寻找驻点作为基本假设,因此难以计及重力对水膜的影响;水膜-冰层模型的求解过程并不包含寻找驻点的步骤,因此与翼型积冰一样,传输线积冰只是水膜-冰层模型在低速环境下的应用.在圆柱体下半部,重力沿表面的分量与空气切应力的方向相同, 因此合力有利于水膜向下风向流动;但在圆柱体上半部,重力沿表面的分量显然起到阻碍水膜流向下风向的作用,这种差别应该是造成冰形关于水平轴不对称的主因.
 |
| 图 5 传输线积冰算例最终冰形的对比图Fig. 5 Comparison of final ice shapes on transmission line |
由水膜-冰层模型计算的翼型积冰表面水膜平均厚度在10-6 m量级,而传输线积冰表面的水膜平均厚度达到了10-4 m量级,在局部区域甚至超过了10-3 m.这是由于当自由流雷诺数小于临界雷诺数2.5×105时,圆柱边界层被认为是层流的,层流分离发生在前缘驻点上下约80°的位置[17],流动图像可以被CFD的计算结果所证实,如图 6所示.在分离点附近由于空气切应力梯度非常大,水膜会在附近积聚,水膜厚度也会显著增加.当水膜厚度与横向尺度相比不再是充分小量时,润滑近似就将失效;同时由于水膜厚度增加引起的局部几何形状变化也会破坏空气边界层从而改变空气流场.因此,分离点附近的水膜流动是采用准定常推进的水膜-冰层模型难以模拟的.参照Messinger模型对水膜溢流的处理,本文采用一种简单的假设来计及这种效应,在某一内部时间步当局部水膜厚度大于某一临界厚度时,形成的质量将并入单元下风向界面的流通量Q之中,也就是超出临界厚度的水膜将发生破裂并被气流带入下游并冻结;这样就在某种程度上保证了质量的守恒性.从图 5a、图 5b的计算冰形与冰风洞试验冰形的吻合程度来看,这种处理方式得到的结果还是令人满意的.
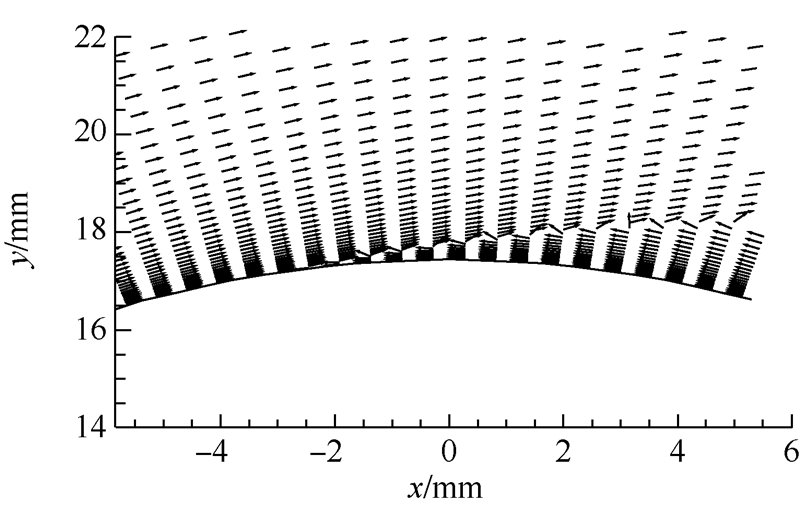 |
| 图 6 CFD计算的圆柱上表面流动分离图像Fig. 6 Vectors image of separated flow on upper part of circle cylinder calculated by CFD |
本文采用基于润滑近似的水膜-冰层模型建立了计算任意二维截面表面积冰的数值方法,在对翼型积冰和传输线积冰进行算例验证后,主要得出以下结论:
1) 水膜-冰层模型具有明显的物理意义和严格的数学形式,在二维积冰问题上的应用是可行的.
2) 采用水膜-冰层模型计算的冰形能够较准确地预测出冰层在翼型上下表面延伸的极限位置以及冰角的位置和形状.
3) 以冰风洞实验冰形为参照,低温环境下基于水膜-冰层模型的翼型冰形曲线是能够与传统Messinger模型比拟的,相对温暖环境下水膜-冰层模型的计算结果要优于Messinger模型的模拟冰形,完全可以满足工程计算的需要.
4) 通过与实验和文献公布的数据比较,水膜-冰层模型同样可以有效预测传输线积冰,计算结果与圆柱体积冰的实验结果相当吻合;这种类型的积冰采用Messinger模型计算十分困难.水膜-冰层模型在空气切应力不占支配作用的低速积冰条件下同样有效,体现了模型的广泛适用性.
| [1] | Messinger B L. Equilibrium temperature of an unheated icing surface as a function of air speed[J].Journal of the Aeronautical Sciences,1953,20(1):29-42 |
| Click to display the text | |
| [2] | Ruff G A, Berkowitz B M.User's manual for the NASA lewis ice accretion prediction code (LEWICE)[R].NASA CR 1990-185129,1990 |
| Click to display the text | |
| [3] | Myers T G, Hammond D W.A mathematical model for atmospheric ice accretion and water flow on a cold surface[J].International Journal of Heat and Mass Transfer,2004,47(25): 54835500 |
| Click to display the text | |
| [4] | Myers T G, Charpin J P F,Chapman S J.The flow and solidification of a thin fluid film on an arbitrary three-dimensional surface[J].Physics of Fluids,2002,14(8):2788-2803 |
| Click to display the text | |
| [5] | Gent R W, Dart N P,Cansdale J T.Aircraft icing[J].Philos Trans R Soc London,Ser A,2000,358:2873-2911 |
| Click to display the text | |
| [6] | Verdin P, Charpin J P F,Thompson C P.Multistep results in ICECREMO2[J].Journal of Aircraft,2009,46(5):1607-1613 |
| Click to display the text | |
| [7] | Verdin P, Charpin J P F.Multi-stepping ice prediction on cylinders and other relevant geometries[J].Journal of Aircraft,2013,50(3):871-878 |
| Click to display the text | |
| [8] | Moriarty J A, Schwartz L W,Tuck E O. Unsteady spreading of thin liquid films with small surface tension[J].Physics of Fluids A,1991,3(5):733-742 |
| Click to display the text | |
| [9] | Brakel T W, Charpin J P F.One-dimensional ice growth due to incoming supercooled droplets impacting on a thin conducting substrate[J].International Journal of Heat and Mass Transfer,2007,50(9/10):1694-1705 |
| Click to display the text | |
| [10] | Wright W B, Gent R W,Guffond D.DRA/NASA/ONERA collaboration on icing research part IIprediction of airfoil ice accretion[R].NASA CR 1997-202349,1997 |
| Click to display the text | |
| [11] | Spalart P R. Trends in turbulence treatments[J].AIAA Paper 2000-2306,2000 |
| Click to display the text | |
| [12] | Shin J, Berkowitz B M.Prediction of ice shapes and their effect on airfoil performance[R].AIAA-91-0264,1991 |
| Click to display the text | |
| [13] | Beaugendre H, Morency F,Habashi W G.Development of a second generation in-flight icing simulation code[J].Journal of Fluids Engineering,2006,128(2):378-387 |
| Click to display the text | |
| [14] | 张强,曹义华, 李栋.采用欧拉两相流法对翼型表面霜冰的数值模拟[J].北京航空航天大学学报,2009,35(3): 351355 Zhang Qiang,Cao Yihua,Li Dong.Numerical method to simulate rime ice accretions on an airfoil[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(3):351-355(in Chinese) |
| Cited By in Cnki (6) | |
| [15] | Wright W B. Validation results for LEWICE2.0[R].NASA/CR 1999-208690,1999 |
| Click to display the text | |
| [16] | Fu P, Farzaneh M,Bouchard G.Two-dimensional modelling of the ice accretion process on transmission line wires and conductors[J].Cold Regions Science and Technology,2006,46(2):132-146 |
| Click to display the text | |
| [17] | 庄礼贤, 尹协远,马晖扬.流体力学[M].合肥:中国科学技术大学出版社,1991:401 Zhuang Lixian,Yin Xieyuan,Ma Huiyang.Fluid mechanics[M].Hefei:Unversity of Science and Technology of China Press,1991:401(in Chinese) |


