高超声速飞行器复杂的强耦合、强非线性和强时变的动力学特性,对飞行器的姿态控制提出了挑战.对再入飞行器来说,再入段的不同阶段使用不同的执行机构组合来进行姿态控制,包括仅使用反推力控制系统(RCS,Reaction Control System),或仅使用气动面控制,或者二者混用.这种控制模式会导致出现2个操纵面控制3个通道的情况,如X-38在从71km下降到39km这一过程中,仅使用两个体襟翼进行控制,通过将同向偏转等价为升降舵偏角,将差动滚转等价为副翼偏角来完成姿态控制[1],这样就不可避免地产生了内动态.目前的研究大多关注在纵向运动中存在内动态的飞行控制[2, 3, 4, 5],实际上在横侧向运动的控制中,也存在内动态,需要设计相应的控制策略以保证系统零动态的稳定.在过去的十几年中,动态逆技术越来越多地应用于飞行控制领域中.主要包括鲁棒动态逆[6, 7, 8]、渐进反馈线性化[9, 10]、基于时标分离的连续动态逆[11, 12, 13]等.应用动态逆方法需要在输入输出线性化时确保其零动态是稳定的.当应用基于逆的控制方法时,如果选择不恰当的输出,也将导致出现不可接受的内动态,输出重定义技术是对目标渐进跟踪时,稳定零动态的非常有效的一种方法[14];另外,通过直接逆对倾侧角控制会导致零动态的不稳定,这种情况下,非最小相位零动态可由渐进反馈线性化技术进行校正.
本文针对再入飞行器大攻角下的姿态控制,其横侧向运动中包含内动态的情况,采用基于输出重定义的动态逆方法稳定零动态,将反馈线性化作用于重定义输出后的系统上,进而设计姿态控制器进行控制.仿真表明该控制器能够稳定零动态,在镇定侧滑角的同时对攻角指令和倾侧角指令具有良好的跟踪性能. 1 再入飞行器姿态控制模型
无动力再入飞行器刚体姿态动力学方程如式(1)所示.定义状态向量x=[α，β，φv，p，q，r]T,分别表示攻角、侧滑角、倾侧角、滚转角速率、俯仰角速率和偏航角速率.其中攻角、侧滑角和倾侧角的微分方程建立在相对坐标系下,姿态角速率微分方程建立在惯性系下.由于重力加速度、航迹倾斜角和航迹速度的变化比姿态和姿态角速率慢得多,因此将它们视为常量.模型中忽略了阻尼导数,这对于高超声速飞行状态下的升力体飞行器来说是可取的假设.忽略操纵面产生的侧力和升力,即形如Yδ和Lδ的导数都置为零,这在应用渐进反馈线性化技术时也是一个常见的假设[15].
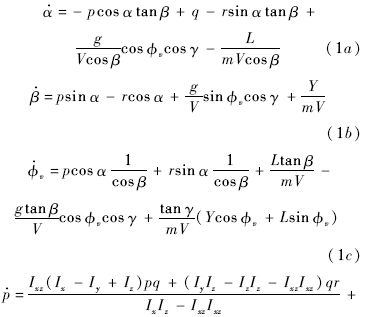
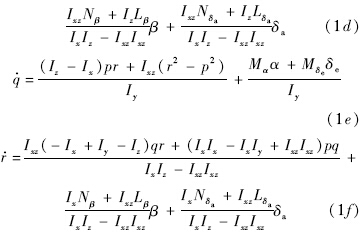
用Δα=α－αT和Δδe=δe－δeT分别表示攻角与配平攻角、升降舵偏角与配平升降舵偏角之间的偏差.配平攻角αT是马赫数的函数,由于马赫数比姿态动力学变化慢很多,因此αT在稳定性分析时视为常量.配平升降舵偏δeT为配平攻角状态下无俯仰力矩时的升降舵偏角,因此M(αT)+M(δeT)=0.所以有
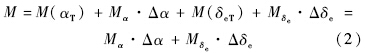
定义f(x)=[f1(x),f2(x)，…,fn(x)]T具有如下形式:
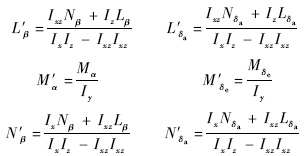
控制分配矩阵为
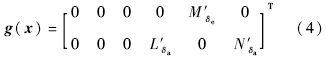
控制量为升降舵偏差角和副翼舵偏角.
考虑一个仿射系统:
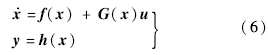
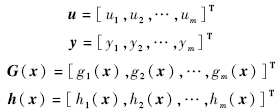
假设系统在x0点的向量相对阶为[ρ1,ρ2,…,ρm],ρ=∑ρi<n,并且存在一个局部坐标转换φ(x):x→(ξ,η),使之前的仿射系统转化为正则形式[7],转化后的正则形式动态方程可用下式表达:
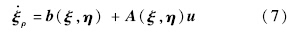
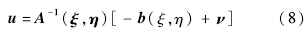
将式(8)代入正则形式得到
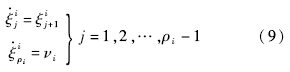
系统输出为
任何输入输出线性化系统的控制律设计都依赖于内动态的性能.假设对外部动态设计了一个渐进跟踪控制律,对于局部跟踪控制问题,内动态的局部输入-状态稳定(ISS,local Input-to-State Stability)即可保证内动态的局部有界[16].而内动态的局部输入-状态稳定的充分条件可通过零动态的概念建立:
假设初始η=0是系统的一个平衡点.这个平衡点渐进稳定,则内动态局部输入-状态稳定.一般来说,具有渐进稳定零动态的系统即为最小相位系统. 2.2 输出重定义
本文采用输出重定义技术[14]使零动态局部稳定.重定义过程分为3步:
1) 找到关于原始输出y的内动态;
2) 令倾侧角φv成为由此得到的内动态的状态变量,以使侧向通道相对阶降为1;
3) 通过输出重定义使零动态(局部)稳定.
在仅体襟翼作用段,只有两个操纵面(m=2),因此只能对两个输出进行解耦跟踪控制.另外,攻角和倾侧角作为影响再入轨迹的关键因素,通常由制导系统作为指令传给控制系统.因此设系统输出为
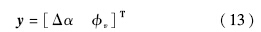
不难看出此时系统的向量相对阶为[2,2],同时ρ=4小于状态向量的个数,应用动态逆将会不可避免地导致内动态.
通过与输出y对应的状态转换Φ(x)=[ξTηT]T,系统转换为正则形式[17].其中
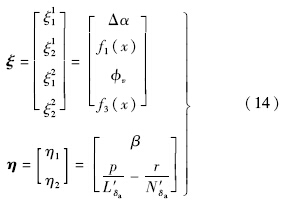
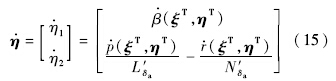
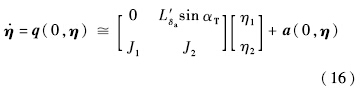
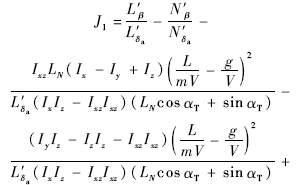
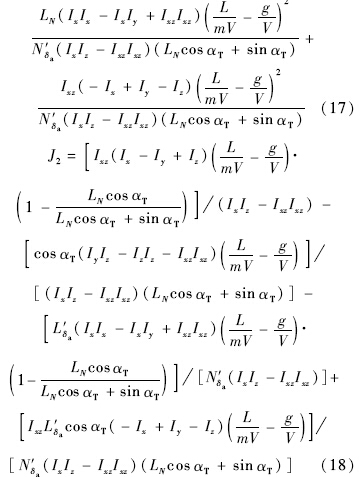
通过如下形式的重定义输出和对参数κ>0的适当选择(本文选择κ=1),系统相对阶被降至[2, 1].
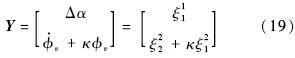
相应的期望输出为
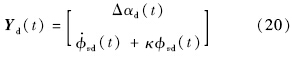
基于这个输出,定义一个二次状态转换,其状态量由输出Y决定:
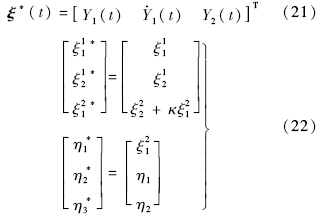
倾侧角ξ12现在是内动态
*的状态变量.使用此转换法,系统可重新表示为一个新的正则形式.假设攻角偏差Δα=ξ11*很小,α≈αT为常值记为α0;β很小,sinβ=β,cosβ=1.相应的内动态可展开为
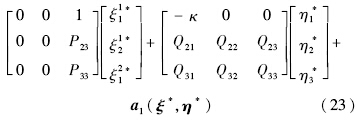
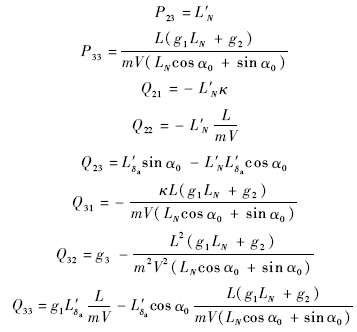
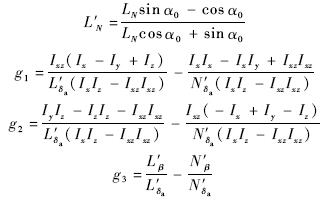
在输出能精确跟踪期望输出的情况下,即Y(t)=Yd(t),内动态具有如下形式:
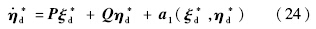
是与期望输出Yd(t)相对应的外部状态的期望.如果式(24)存在一个可接受的解ηd*(t),或者一个使ηd*(t)有界的初始状态,则把ηd*(t)称为理想内动态(IID,Ideal Internal Dynamics).现在使用输出Y的实际重定义:
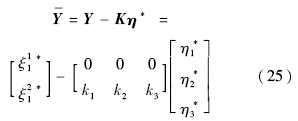
重定义输出的期望为
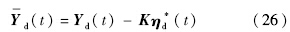
基于实际重定义输出,进行如下的状态转换,得到正则形式的动态方程.其中
根据状态转换式(27),式(26)中的输出的期望可由如下状态的期望表达:
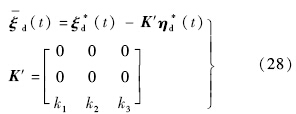
考虑理想跟踪情况,即在有限的时间T>0之后实现对重定义输出的理想跟踪,此时Y(t)≡Yd(t),或对任意t≥T,有ξ(t)≡ξd(t).在此情况下,可得到误差变量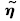
=η－ηd*的动态特性为
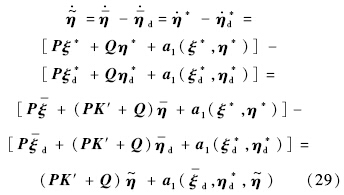
选择适当的k,使[PK′+Q]的特征值具有负的实部以使零动态局部渐进稳定,从而可保证内动态的局部输入-状态稳定.由于系统状态可控,任意极点配置是可以实现的.另外,方程(29)说明了渐进跟踪是如何实现的.在使用适当的控制律后,即可实现渐进跟踪,因此可得Y(t)→Yd(t).在此情况下,误差变量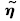的实际动态特性渐进接近理想动态特性,此时式(29)成立.由此,内动态渐进逼近理想内动态,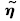→0.由式(25)和式(26),这又导致Y(t)→Yd(t),最后,由于式(19)和式(20)中的定义,得到y(t)→yd(t).
考虑将重定义输出后的系统误差动态的极点配置在[－10,－0.05±0.1i]以使原始系统的零动态局部渐进稳定,并计算得到k1=1.19,k2=－32,k3=－17.6.
由于理想内动态直接影响在原始输出下的跟踪性能,之前提到的渐进跟踪只能在某些特殊情况下实现,即,对于某些有界的ξd*(t),ηd*(t)是方程(24)的解.由于得到此通解是很困难的[6],因此选择仅在倾侧角为阶跃输入时求解方程(24),即φvd(t)=φv,const,φv,const为一常值.另外,方程(24)的稳态解也可被用作理想内动态的解,这样可避免稳态跟踪误差. 3 基于输出重定义的动态逆控制器
根据之前的推导,重定义输出式(25)可在初始的坐标下写成如下形式:
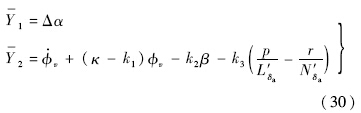
对于此重定义输出进行如式(31)所示的坐标转换φ(x):x→(ξ,η),根据式(7),得到系统动态的正则形式表达式(32):
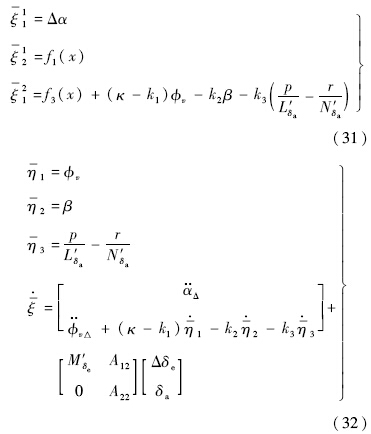
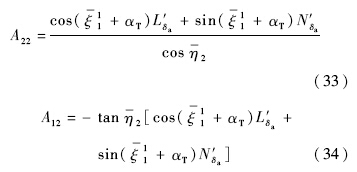
表达式中与输入不相关部分,经化简,
具有如下形式:
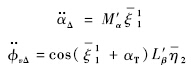
对于有界的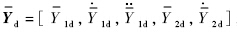
,定义跟踪误差:
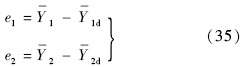
定义伪控制量:
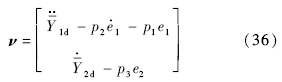
由式(7)所示的正则形式动态方程得到动态逆控制律:
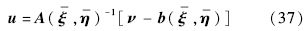
将上式展开并进行参数敏感度分析,发现升降舵控制律中虽耦合了横侧向通道的参数,但都是小量,在忽略了这些量之后控制效果没有明显的变化,因此为了简化控制器的形式,去除了升降控制律中的横侧向参数,而副翼控制律中的纵向通道参数(如攻角、滚转角速率等)的影响不可忽略,需要保留.至此,得到基于输出重定义的动态逆控制律:
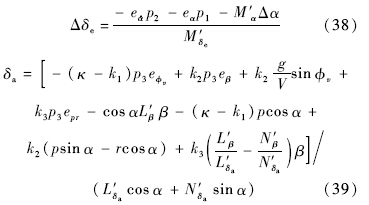
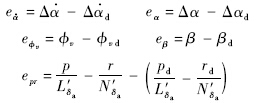
从该控制器的推导过程可以看出,并未对 3个通道进行解耦,所以该控制器严格意义上并不算是解耦控制,这与高超声速飞行器大攻角再入时纵向与横航向通道间强耦合的特点也是一致的. 4 仿真结果
为了验证本文所设计的控制器,在飞行条件:Ma=20.2,H=55km,初始攻角α=10°,初始侧滑角β=0°下,为了对阶跃指令进行跟踪,令攻角偏差角跟踪指令Y1d=5°,倾侧角跟踪指令Y2d=20°,并保持零侧滑角.控制器参数取p1=190,p2=45,p3=30,k1=1.2,k2=-32,k3=18,仿真时间为60s.为了更好地说明本控制器的优越性,将与RCS独立控制时的结果进行对比,先用本控制器生成需用力矩,然后把需用力矩经过转化,生成RCS的开关指令,对应的RCS控制参数为:p1=260,p2=28,p3=700,k1=9,k2=-300,k3=-400.仿真结果如图 1~图 7所示.
 |
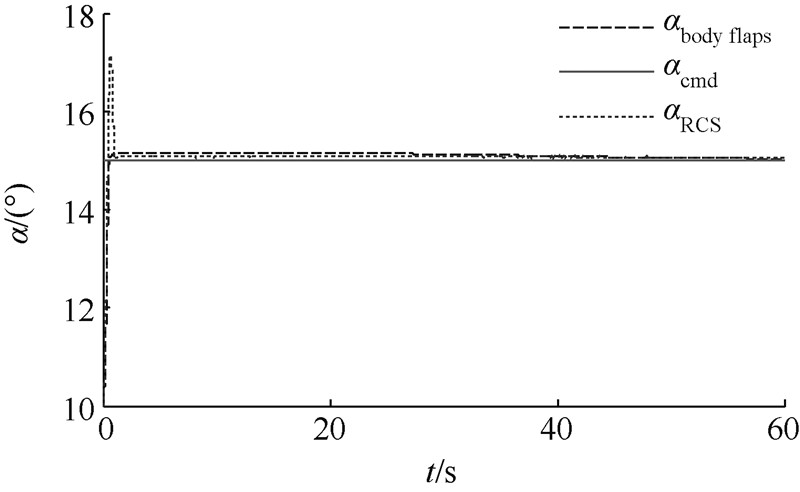| 图 1 攻角跟踪结果对比Fig. 1 Response of angle of attack |
图 1~图 3为攻角、侧滑角和倾侧角的跟踪曲线.
 |
| 图 2 侧滑角跟踪结果对比Fig. 2 Response of sideslip angle |
 |
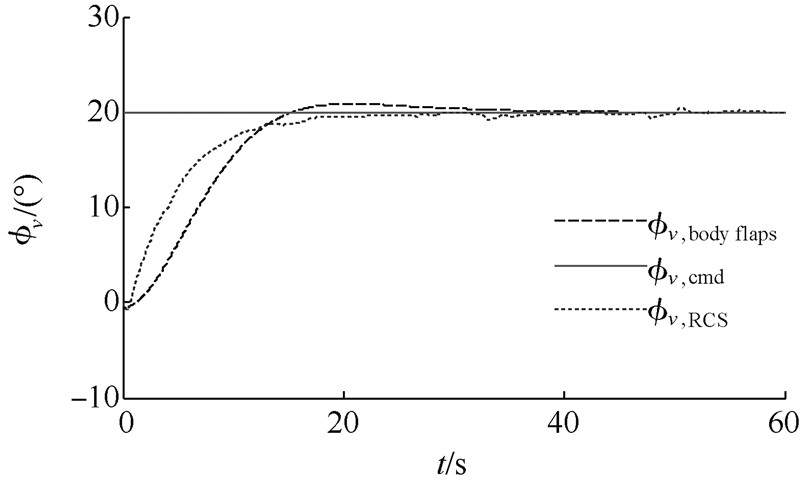| 图 3 倾侧角跟踪结果对比Fig. 3 Response of bank angle |
图 4和图 5分别为气动舵面控制与RCS控制的3个姿态角速率.
 |
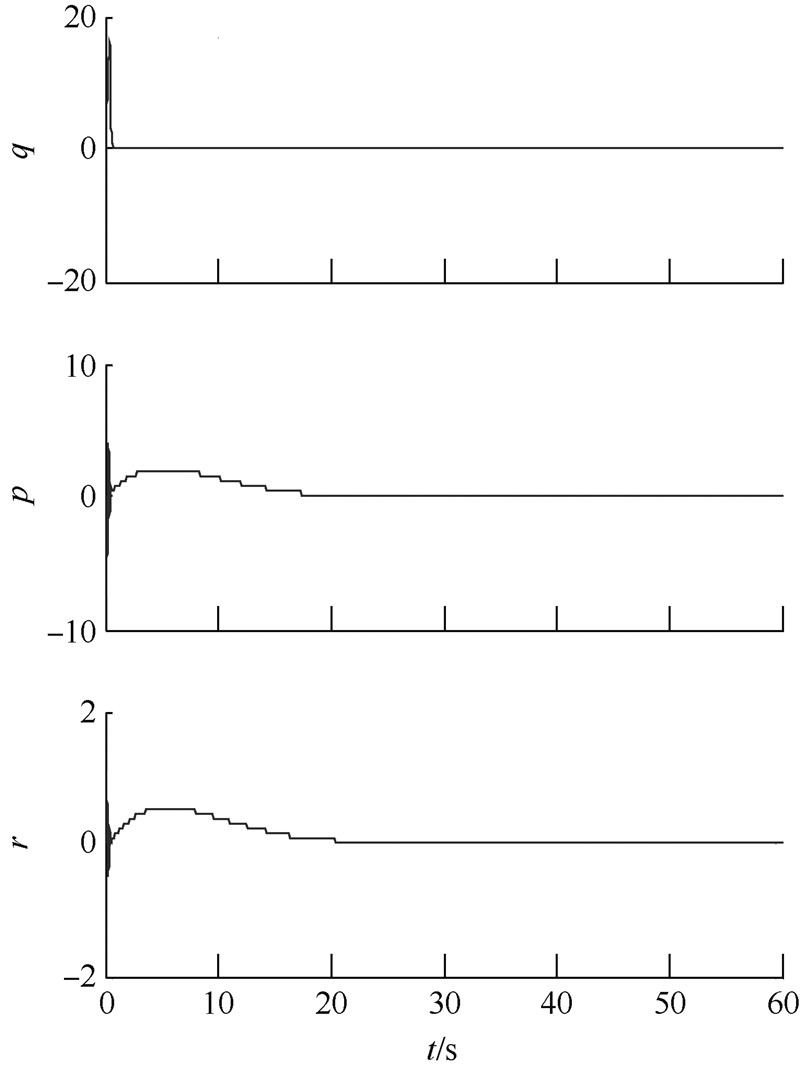| 图 4 舵面控制下3个姿态角速率变化曲线Fig. 4 Attitude angle rates for actuator control |
 |
| 图 5 RCS控制下3个姿态角速率变化曲线Fig. 5 Attitude angle rates for RCS control |
图 6为2个舵面的偏转角度.
 |
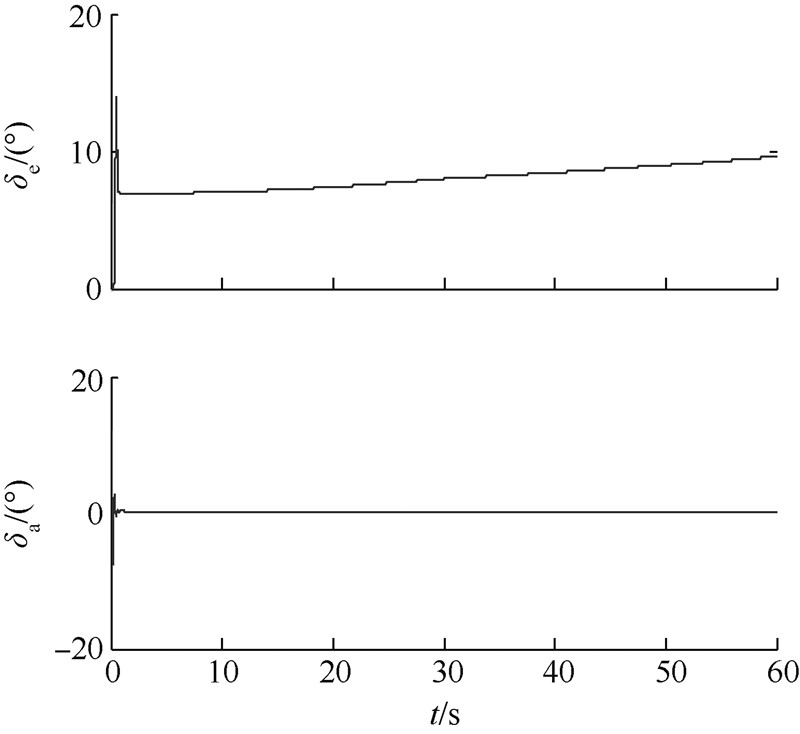| 图 6 舵面偏转角Fig. 6 Actuator angles |
图 7为气动舵面控制时内动态的变化.
 |
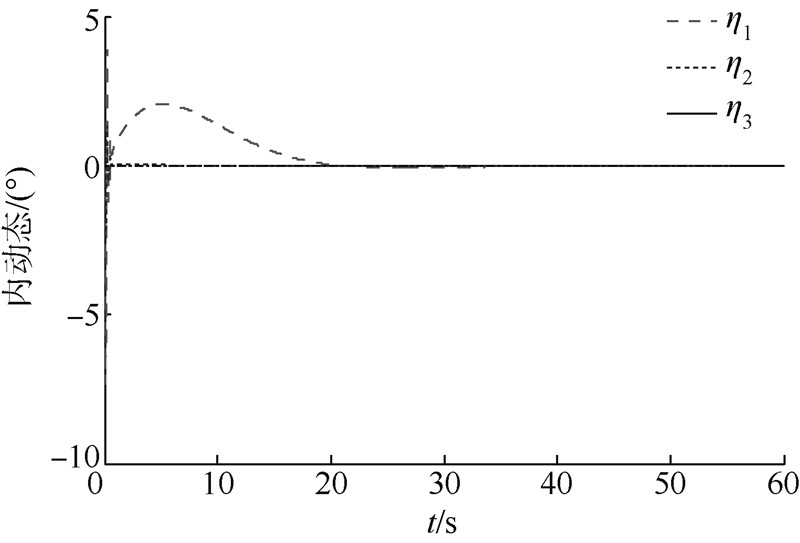| 图 7 内动态的变化曲线Fig. 7 Response of internal dynamics |
从图 1~图 3和图 7中可以看出,在本文所设计的控制器作用下,系统的内动态是稳定的,攻角与倾侧角能很好地跟踪制导指令,与此同时镇定侧滑角在0°左右.与RCS作用相比,跟踪快速性相差不大,并且超调更小. 5 结 论
对于大多数飞行器外形,在大攻角条件下方向舵形式的操纵面是无效的,而且往往希望尽量少地使用RCS来节省推进剂.因此,仅剩副翼和升降舵形式的气动面可用作控制.增加气动面虽然可以增加控制量的数量,但同时会增加结构重量和整个系统的复杂度.本文针对该问题提出一种基于输出重定义的大攻角再入飞行器动态逆姿态控制方法.由于在特定飞行阶段仅有两个舵面起作用,因此不可避免会产生内动态.通过输出重定义技术稳定零动态,再对重定义输出后的系统进行反馈线性化,从而设计控制器进行控制.仿真结果验证了内动态的稳定性,并显示出对指令良好的跟踪性能.通过与RCS单独控制进行比较,可以发现该控制器性能与RCS相当,但由于采用气动舵面进行控制,可以大大节省燃料,从而减小飞行器的结构复杂度,增大有效载荷.通过本文的控制策略开发最小组合的操纵面,最终使再入飞行器姿态控制系统具有更简单的结构且耗费更少的能量.
| [1] | Ito D,Georgie J,Valasek J.Reentry vehicle flight controls design guidelines:dynamic inversion[R].NASA/TP-2002-210771,2002 |
| [2] | 李惠峰,李昭莹.高超声速巡航飞行器在线自适应反馈控制设计[J].北京航空航天大学学报,2010,36(11):1382-1386 Li Huifeng,Li Zhaoying.Adaptive feedback control design for hypersonic cruise flight vehicle[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(11):1382-1386(in Chinese) |
| Cited By in Cnki (3) | |
| [3] | 闫晓东,唐硕.基于反馈线性化的H-V返回轨道跟踪方法[J].宇航学报,2008,29(5):1546-1550 Yan Xiaodong,Tang Shuo.Entry trajectory tracking law for suborbital launch vehicle via feedback linearization[J].Journal of Astronautics,2008,29(5):1546-1550(in Chinese) |
| Cited By in Cnki (9) | |
| [4] | Kim S G,Tahk M J.Output redefinition based on robust zero dynamics[R].AIAA-98-4493,1998 |
| Click to display the text | |
| [5] | Gopalswamy S,Hedrick J K.Control of a high performance aircraft with unacceptable zero dynamics[C]//American Control Conference.Piscataway,NJ:IEEE,1992:1834-1838 |
| [6] | Ito D,Ward D T,Valasek J.Robust dynamic inversion controller design and analysis for the X-38[R].AIAA-2001-4380,2001 |
| [7] | MacKunis W,Patre P M,Kaiser M K,et al.Asymptotic tracking for aircraft via robust and adaptive dynamic inversion methods[J].IEEE Transactions on Control Systems Technology,2010,18(6):1448-1456 |
| [8] | Reiner J,Balas G J,Garrard W L.Robust dynamic inversion for control of highly maneuverable aircraft[J].Journal of Guidance,Control,and Dynamics,1995,18(1):18-24 |
| Click to display the text | |
| [9] | Jensen H B,Wisniewski R.Quaternion feedback control for rigid-body spacecraft[R].AIAA-2001-4338,2001 |
| [10] | Parker J T,Serrani A,Yurkovich S,et al.Approximate feedback linearization of an air-breathing hypersonic vehicle[C]//AIAA Guidance, Navigation,and Control Conference.Reston:AIAA,2006:1-20 |
| [11] | Snell S A,Enns D F,Arrard W L.Nonlinear inversion flight control for a supermaneuverable aircraft[J].Journal of Guidance,Control,and Dynamics,1992,15(4):976-984 |
| Click to display the text | |
| [12] | Naidu S D,Calise A J.Singular perturbations and time scales in guidance and control of aerospace systems:a survey[J].Journal of Guidance,Control,and Dynamics,2001,24(6):1057-1078 |
| Click to display the text | |
| [13] | Reiner J,Balas G J,Garrard W L.Flight control design using robust dynamic inversion and timescale separation[J].Automatica,1996,32(11):1493-1504 |
| Click to display the text | |
| [14] | Gopalswamy S,Karl H J.Tracking nonlinear non-minimum phase systems using sliding control[J].International Journal of Control,1993,57(5):1141-1158 |
| Click to display the text | |
| [15] | Lane S H,Stengel R F.Flight control design using nonlinear inverse dynamics[C]//American Control Conference.Piscataway,NJ:IEEE,1986:587-596 |
| [16] | Slotine J E,Li W P.应用非线性控制[M].程代展译.北京:机械工业出版社,2009 Slotine J E,Li W P.Applied nonlinear control[M].Translated by Cheng Daizhan.Beijing:China Machine Press,2009(in Chinese) |
| [17] | Wallner E M,Well K H.Attitude control of a reentry vehicle with internal dynamics[J].Journal of Guidance,Control,and Dynamics,2003,26(6):846-854 |
| Click to display the text |