随着对混沌系统研究的不断深入,已经有越来越多的针对混沌系统的控制和同步方法被提出来,并得到了有效的验证和应用[1, 2, 3].但是目前绝大多数的研究仅限于整数阶混沌系统,而整数阶系统只是分数阶系统的一个特例,分数阶系统才具有真正意义上的普遍性[4, 5].
近年来,随着混沌控制研究热潮的兴起,对分数阶混沌系统的研究也引起了广泛的关注.当前对整数阶混沌系统设计控制器之后进行稳定性分析的一般方法是运用Lyapunov稳定性理论,而对于分数阶系统的稳定性分析目前还基本依赖于分数阶系统稳定性理论和分数阶系统稳定性理论与Lyapunov稳定性理论相结合的方法[6, 7].
从近年分数阶混沌系统的研究现状来看,在分数阶混沌系统的同步控制领域已经取得了大量的成果.文献[8]采用类Lyapunov稳定性理论,设计了分数阶混沌系统同步控制器;文献[9]对两个耦合的分数阶混沌系统设计了主动非线性反馈控制方案,实现了两个系统间的相位同步,但该方法只适应于理想的分数阶混沌系统;文献[10]采用滑模自适应控制方法对分数阶混沌系统设计了同步控制器,能够实现投影同步,但该方法没有考虑混沌系统中不确定因素的影响,对于现实系统来说缺乏实际意义;文献[11]根据分数阶混沌系统稳定性理论,设计了一种基于扩展分数阶卡尔曼滤波的分数阶混沌保密通信系统,但考虑的同步对象系统仍是理想的;文献[12]采用根据驱动系统构建相应响应系统的方法,在考虑不确定因素影响的情况下,对不确定项进行了自适应估计,设计了一种非线性自适应控制器.所设计的控制器不需要知道不确定项上界,该控制器结构简单,控制系统对包括干扰在内的系统不确定性具有较强的鲁棒性.但是该方法并不适用于分数阶混沌系统的同步,且存在响应系统结构依赖于驱动系统结构的问题.
本文研究的目的就是针对文献[8, 9, 10, 11, 12]各自存在的不足,设计适用于不确定分数阶混沌系统同步的控制策略.
1 问题描述
考虑如下分数阶系统[13]:
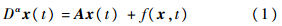
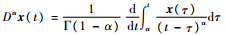表示Riemann-Liouville分数阶导数;Γ(·)为Gamma函数;A∈Rn×n为系统参数矩阵;x为状态向量;f(x)为光滑的非线性函数,并假设其满足Lipchitz条件,即
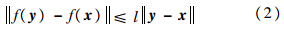
构建如下带控制输入的响应系统:
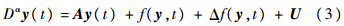
本文研究的目的就是要设计同步控制器U,使得当t→∞时:
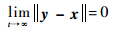
符号约定:
;若A为常数矩阵,则有
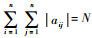,N为一正数.
2 控制器设计和稳定性分析
根据Matignon提出的分数阶线性系统稳定性理论,有如下引理[14]:
引理1 考虑分数阶系统:
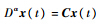
1)|arg(λi)|>απ2时,分数阶系统是渐近稳定的;
2) |arg(λi)|≥απ2时,分数阶系统是稳定的.
分数阶线性系统的稳定区域如图 1所示.
 |
| 图 1 分数阶系统状态空间稳定区域图 Fig. 1 Fractional-order system state space stability diagram |
显然,当0<α<1时,只要系统的参数矩阵C的所有特征值的实部都不大于零,则分数阶系统是渐近稳定的.
定义同步误差e=y－x,e=(e1,e2,…,en)T,可以得到分数阶误差系统方程为
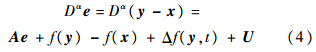
参考文献[10],选择滑模面:
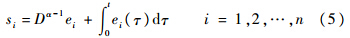
对上式两边求导得s·i=Deiα+ei,当系统发生滑模运动时,需满足si=0,和s·i=0,因此有
根据引理1可知,式(6)是渐近稳定的,也即驱动系统和响应系统将趋于同步,又由滑模运动对干扰的不敏感特性可知,系统对干扰具有较好的鲁棒性.
设计如下控制器:
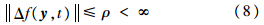
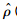表示ρ的估计,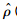(0)∈R+.定理1 采用式(7)所表示的控制器和式(9)所表示的自适应律时,驱动系统式(1)和响应系统式(3)达到同步,即从任意初始条件出发的误差轨迹将收敛于零.
证明 将式(7)代入式(4)可得
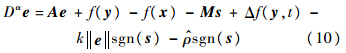
构造Lyapunov函数为
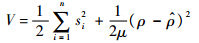
对V关于时间求导
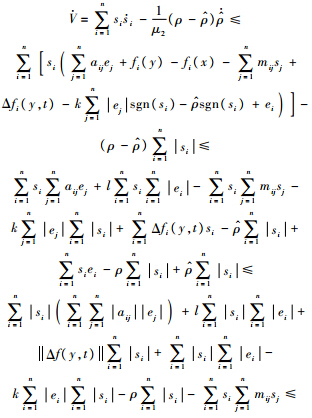
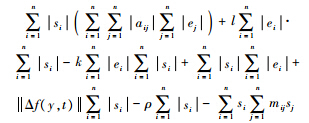
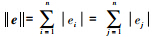,则
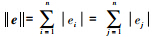
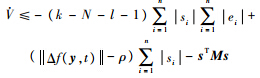
由V≥0,V·≤0知V单调递减且有下界,所以V存在有限的极限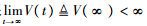
即
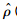均有界.由式(12)可知,s2≤－V·/m,两边积分可得
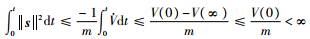
由以上分析可知,从任意初始条件出发的误差系统轨迹均满足滑模到达条件,在所设计的自适应控制器的作用下,可在有限时间内到达或趋近滑模面s=0,误差系统将收敛于零,也即驱动系统和响应系统趋于同步.
3 数值仿真
基于改进的Adms-Bashforth-Moulton理论,文献[15]提出了分数阶混沌系统仿真算法,本文采用该算法进行了仿真计算.考虑以分数阶Arneodo混沌系统作为驱动系统:
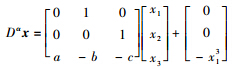
文献[8]分析了该系统的动力学行为,当参数为a=5.5,b=3.5,c=0.4,阶次α=0.9时,该分数阶系统在2.7维具有混沌吸引子.
构造响应系统如下:
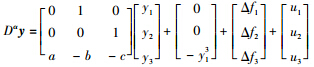
系统不确定部分为
根据定理1可得如下控制器:
ρ^的自适应律为
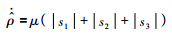
驱动系统和响应系统状态的初始值分别选择为(0.1,0.5,0.1)T和(1,0.1,1.2)T,分数阶次均取α=0.9,取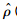(0)=0,μ=0.8,反馈增益取mi=2,控制增益k根据给出的定义,计算正数N和Lipchiz常数l,选择k=240,计算步长取0.001s,仿真结果如图 2所示
 |
| 图 2 仿真曲线 Fig. 2 Simulation curves |
从仿真结果可以看出,在考虑不确定项Δf(y,t)的情况下,驱动系统式(1)和构建的响应系统式(3)实现了同步,参数ρ的估计值最终收敛到一个常数.
4 结 论
本文在前期研究了现有的不确定分数阶混沌系统的同步方法，在对已有研究成果的基础上，提出了一种滑模自适应同步控制法，从分析过程及数值仿真可知：
1) 系统存在的不确定性对分数阶混沌系统的同步存在较大影响；
2) 选取合适的滑模曲面，可将滑模控制方法引入分数阶混沌系统的同步控制中，进而可以直接采用Lyapunov稳定性理论对系统的稳定性进行分析；
3) 采用自适应技术估计集总干扰上界，相较其他分别处理系统不确定性的方法，可减小计算量，简化控制器结构；
4) 利用滑模控制及自适应控制的特性，能提高控制系统的鲁棒性能.
| [1] | 石晓荣,张明廉.一种基于混沌神经网络的拟人智能控制方法[J].北京航空航天大学学报,2004,30(9):889-892 Shi Xiaorong,Zhang Minglian.Human-imitating control based on chaotic neural networks[J].Journal of Beijing University of Aeronautics And Astronautics,2004,30(9):889-892(in Chinese) |
| Cited By in Cnki (8) | |
| [2] | 张俊锋,沈云琴,张晓丽.利用滑模控制实现不确定混沌系统投影同步[J].计算机测量与控制,2011,19(8):1912-1914 Zhang Junfeng,Sheng Yunqin,Zhang Xiaoli.Projective synchro-nization of chaotic system with uncertainties based on sliding mode control[J].Computer Measurement & Control,2011,19(8):1912-1914(in Chinese) |
| Cited By in Cnki (1) | |
| [3] | Kinzel W,Englert A,Kanter I.On chaos synchronization and secure communication[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,2010,368(1911):379-389 |
| Click to display the text | |
| [4] | 李东,邓良明,杜永霞,等.分数阶超混沌Chen系统和分数阶超混沌Rossler系统的异结构同步[J].物理学报,2012,61(5):050502-1-9 Li Dong,Deng Liangming,Du Yongxia,et al.Synchronization for fractional order hyperchaotic Chen system and fractional order hyperchaotic Rossler system with different structure[J].Acta Physica Sinica,2012,61(5):050502-1-9(in Chinese) |
| Cited By in Cnki (11) | |
| [5] | 谭文,张敏,李志攀.分数阶互联电力系统混沌震荡及其同步控制[J].湖南科技大学学报,2011,26(2):74-77 Tan Wen,Zhang Min,Li Zhipan.Chaotic oscillation of interconn-ecred power system and its synchronization[J].Hunan Univers-ity of Science & Technology,2011,26(2):74-77(in Chinese) |
| Cited By in Cnki (2) | |
| [6] | 胡建彬,韩焱,赵灵冬.分数阶系统的一种稳定性判定定理及在分数阶统一混沌系统同步中的应用[J].物理学报,2009,58(7):4002-4007 Hu Jianbin,Han Yan,Zhao Lingdong.A stability theorem about fractional systems and synchronizing fractional unified chaotic systems based on the theorem[J].Acta Physica Sinica,2009,58(7):4002-4007(in Chinese) |
| Cited By in Cnki (15) | |
| [7] | 孙光辉.分数阶混沌系统的控制及同步研究[D].哈尔滨:哈尔滨工业大学,2010 Sun Guanghui.The research on the fractional chaos synchronizat-ion and control[D].Harbin:Harbin Institute of Technology,2010(in Chinese) |
| [8] | 马铁东,江伟波,浮洁,等.一类分数阶混沌系统的自适应同步[J].物理学报,2012,61(16):160506-1-6 Ma Tiedong,Jiang Weibo,Fu Jie,et al.Adaptive synchronization of a class of fractional-order chaotic systems[J].Acta Physica Sinica,2012,61(16):160506-1-6(in Chinese) |
| Cited By in Cnki (8) | |
| [9] | Zaid O.A note on phase synchronization in coupled chaotic fractional order systems[J].Nonlinear Analysis:Real World Applications,2012,13(2):779-789 |
| Click to display the text | |
| [10] | 黄丽莲,齐雪.基于自适应滑模控制的不同维分数阶混沌系统的同步[J].物理学报,2013,62(8):080507-1-7 Huang Lilian,Qi Xue.The synchronization of fractional order chaotic systems with different orders based on adaptive sliding mode control[J].Acta Physica Sinica,2013,62(8):080507-1-7(in Chinese) |
| Cited By in Cnki (4) | |
| [11] | Arman K B,Fallahi K,Pariz N,et al.A chaotic secure communi-cation scheme using fractional chaotic systems based on an exte-nded fractional Kalman filter[J].Communications in Nonlinear Science and Numerical Sumulation,2009,14(3):863-879 |
| Click to display the text | |
| [12] | 邓玮,方洁,吴振军,等.含有不确定项的混沌系统自适应修正函数投影同步[J].物理学报,2012,61(14):140503-1-7 Deng Wei,Fang Jie,Wu Zhenjun,et al.Adaptive modified function projective synchronizatio of a class of chaotic systems with uncertainties[J].Acta Physica Sinica,2012,61(14):140503-1-7(in Chinese) |
| Cited By in Cnki (6) | |
| [13] | Hifer R.Applications of fractional calcus in physics [M].New Jersey:World Scientific,2001:44-47 |
| [14] | Matignon D.Stability results for fractional differential equations with application control processing[J].IMACS,IEEE-SMC,1996,17(6):963-968 |
| [15] | Wang J M,Xiong X H,Zhang Y B.Extending synchronization scheme to fractional-order Chen systems[J].Physica A:Statistical Mechanics and its Applications,2006,370(2):279-285 |
| Click to display the text |