自2007年起,美国次贷危机爆发,引发了全球金融业大地震,迈阿密山谷银行、华盛顿互惠银行、美联银行等商业银行以及贝尔斯登、雷曼兄弟等投资银行相继破产。此后,如何提高银行在金融危机中的自救能力既是银行与政府监管部门亟需解决的难题,也是学术界的研究热点。在此背景下,自救债务工具应运而生。巴塞尔协议Ⅲ对银行的资本金提出了新的要求,并推荐可将应急资本作为银行的风险管理工具。或有可转债(Contingent Convertible Bonds, CoCos)是其中一种重要的应急资本。在银行面临预先设定的财务困境或者生存危机时,或有可转债可以自动转换成股票或者其票面价值被减记,从而减轻银行的财务负担,提高其自救能力。
自从2009年11月至今,许多银行,诸如英国劳埃德银行集团、荷兰合作银行、瑞士信贷集团、德国德意志银行等,已发行了或有可转债。随着越来越多的银行参与发行或有可转债,其合约设计与定价方法成为研究热点。或有可转债定价模型或基于现金流,或基于股价,这取决于触发事件的定义。De Spiegeleer和Schoutens将触发事件归纳为四类:会计触发、市场触发、监管触发、多变量触发。他们基于市场触发事件与障碍期权的定价公式给出了或有可转债的显式定价公式[1]。Corcuera等设计并分析了票息可撤销的或有可转债并给出其显式定价公式[2]。Corcuera等应用结构化方法得出具有延期风险的或有可转债的定价公式,所谓延期风险是指CoCos发行方不能于事先约定的赎回日期回购债券[3]。秦学志等以权益比率为触发器,利用二叉树模型与风险中性定价原理给出离散时间下的或有可转债定价方法[4]。秦学志等以股价为触发器,设计了含股权回售与赎回条款的或有可转债,并引入Jarrow-Turnbull模型确定生存概率,给出CoCos的定价公式[5]。
以上这些定价模型均建立在经典市场中,目前未有文献涉及分形市场中的或有可转债定价模型。事实上,Mandelbrot用重标极差(R/S)方法检测经济时间序列的长程自相关性,首次说明了资产市场中长程相关性的重要性[6]。Peters首先提出分形市场假说(FMH),与有效市场假说不同,FMH试图从投资者行为角度去解释价格变动,认为投资者对信息的理解存在不同的时间尺度,资产价格变化呈现非线性。他利用分形学、R/S方法、非线性动态模型理解资产价格变动[7]。Shiryaev对美国金融市场中股价和汇率的记忆性和自相似性给予了详细描述,并提供了实证支持[8]。范英和魏一鸣基于R/S方法得出沪深股指在不同的时间标度下,收益率序列的Hurst指数在0.63与0.72之间[9]。郝清民应用R/S方法揭示中国股市主要指数和个股收益序列中都存在一定程度的长记忆效应[10]。而Hurst指数H满足1/2 < H < 1的分数布朗运动(fractional Brownian motion, fBm)具有长记忆性、自相似性、保持运动趋势性等非线性性质,所以,用1/2 < H < 1的fBm替代布朗运动驱动风险资产价格变化符合收益率序列的统计特性。
事实上,若股价动态方程由fBm驱动,则股价呈现长记忆性,如果再假设市场无交易成本并且投资者可以无限快速地连续交易,则金融市场存在套利机会。为了使得基于fBm建模的金融市场无套利,众多学者采用其他方法或者引入其他限制条件,比如fBm的正则化方法,假设单个投资者任意两次相连的交易之间存在一定的时间间隔,引入交易成本,引入投资者风险偏好与经济学均衡思想[11][12][13][14]79-110。
文章意在将经典市场中的或有可转债定价公式推广到分形市场,在此市场中,标的股价呈现长记忆性与分形性。作此推广的原因是:在上交所交易的中资银行股票收益率序列存在较弱的长程自相关性。文章用分数布朗运动驱动的随机微分方程描述银行股价动态过程,并分析标的股票收益率序列的长程自相关性如何影响CoCos的价格。结果表明,虽然标的股票收益率序列的长程自相关性较弱,但由于CoCos为中长期衍生证券,其对CoCos价格的影响并不能被忽略;特别地,其对CoCos股权关联部分价值的影响较显著。同时,文章给出了分数布朗运动下障碍期权价值的求解过程以及显式定价公式,并且定价公式不存在经济含义不清晰的问题[15]。
二、或有可转债合约描述首先,假定某上市银行在时间t=0发行了或有可转债。用(St)t≥0表示该银行的股票价格,用(Vt)t≥0表示该或有可转债的价格。假设或有可转债合约的面值为M,到期时间为T。一旦股票价格(St)t≥0在或有可转债的续存期内达到预先设定的障碍水平SB,则触发事件发生,即该触发为市场触发。与De Spiegeleer和Schoutens使用的方法一致,这里假设当触发事件发生时,一定比例的面值αM将被转换为股权,而剩下的部分将被保留为普通债券,其面值为(1-α)M,到期时间仍然为T[1]。
(情况1) 如果或有可转债合约不支付票息,则其在到期时间T的价值为

|
(1) |
其中:Cr=αM/CP,为转换比例;CP为转换价格,这两者事先在合约中约定。变换式(1)后可得

|
(2) |
其中:1{trigger}=1{min(St)0≤t≤T ≤ SB}=1-1{St>SB, ∀0≤t≤T},这里1A(·)是示性函数。从式(2)可以看出,零息票CoCo合约可被分解为两部分:零息票普通债券与向下敲入远期合约。
(情况2) 1如果或有可转债合约分别在时间ti支付票息ci,i=1, 2, …, n,一旦触发事件发生,则原票息ci将降为(1-α)ci。所以,该含票息支付的CoCo合约可以被分解为

|
(3) |
其中:向下敲入数字期权源于市场触发事件发生后票息ci的减损。
注1:障碍水平SB根据银行的资本结构和最低资本充足率而预先设定。文章关注如何为或有可转债定价,不是关注如何设定合约的障碍水平SB以使得银行的资本充足率满足监管要求,所以文章直接给定SB。
三、或有可转债的定价首先,假设市场不存在卖空限制,不存在交易成本与税收。假设单个投资者任意相连的两次交易之间存在一定的时间间隔,则市场不存在可供套利的交易策略[12]。
令BH=(BtH)t≥0是定义在概率空间(Ω, F, {Bt}t≥0T, P)上的分数布朗运动,其中Hurst指数H∈(1/2, 1),P是真实概率测度,Ft=σ(BsH, 0≤s≤t),F0是平凡的,F=FT。
假设标的银行的股价服从如下随机微分方程

|
(4) |
其中:σ>0为常数;μt关于Ft适应。令BtH=

|
(5) |
并且原来的概率空间(Ω, F, {Ft}t≥0T, P)重写为(Ω, F, {Ft}t≥0T, P),其中Ft=σ(BsH, 0≤s≤t),F0平凡,F=FT,μt关于Ft适应。
现在的任务转换为找到合适的μt使得P是“风险中性概率测度”,在此测度下,任何资产的期望收益率等于无风险利率r。在鞅定价框架下,市场无套利保证了等价鞅测度的存在,而当市场不完备时,这样的等价鞅测度不惟一。当股价动态方程由fBm驱动时,在投资者不能连续交易的假定下,市场无套利但不完备,从而风险中性概率测度P存在但不惟一。用Rostek提出的基于偏好的均衡定价方法寻找μt,从而确定P[14]79-110。该方法直接假设所有投资者都是风险中性的,他们拥有关于价格的历史信息并使用这些信息。该方法利用了fBm的记忆性,并已经被众多学者用于分数布朗运动环境下的衍生品定价,如对认股权证进行定价[16]。该方法的理论基础概述如下所示[14]79-110。
引理1. 令BH=(BtH)t∈R为分数布朗运动,其中Hurst指数H∈(0.5, 1)。在时间t,与该分数布朗运动具有相同历史路径的等价类定义如下:
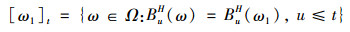
|
(6) |
Ft=σ(BuH, u≤t)亦表示投资者在时间t能获得的关于fBm的全部历史信息,则BsH, s>t基于历史信息Ft=σ(BuH, u≤t)的条件分布为正态分布,且条件期望和条件方差分别为
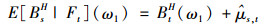
|
(7) |
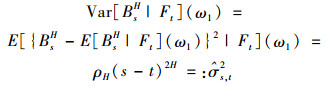
|
(8) |
其中:

|
(9) |
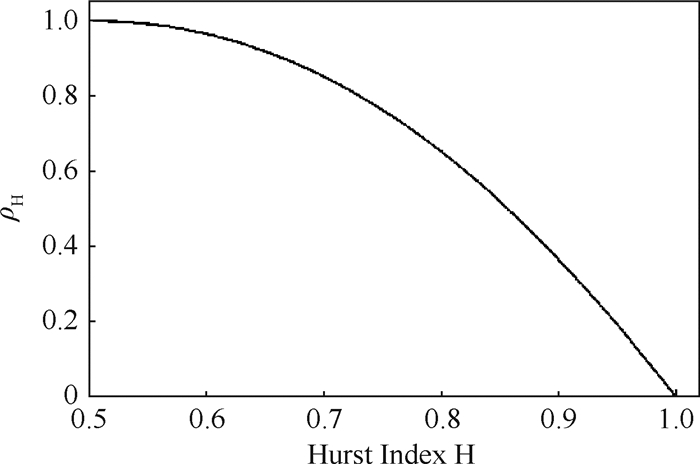
这里ρH如图 1所示,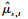
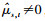

|
图 1 ρH随着H变化的图形[14]79-110 |
分数布朗运动具有记忆性,继续考虑其基于历史路径的条件过程。用
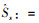

|
(10) |
两边取对数,可得

|
(11) |
根据引理1,如下三个式子成立:
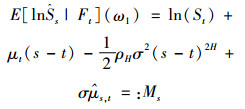
|
(12) |
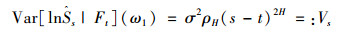
|
(13) |
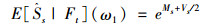
|
(14) |
基于观测[ω1]t和给定的到期时间T,可知

|
(15) |
原因如下。风险中性投资者可以在时刻t花St金额买入一份股票,基于观测[ω1]t,该股票在时刻T的期望价格为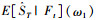

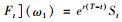
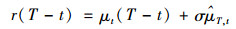
|
(16) |
在此框架下,可以为第二部分描述的或有可转债定价。用C(t, S)表示到期时间为T的障碍期权在时刻t的价值,并且假定该障碍期权的障碍还未被触发。则C(t, S)满足如下的偏微分方程(PDE)[14]79-110
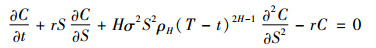
|
(17) |
障碍期权的障碍特性通过边界条件进入方程,不同的边界条件刻画不同的障碍期权。式(3)中CoCos各组成部分的价值由第四部分的定理给出。最终得到CoCos显式定价公式如定理1所示。
定理1. 用V(t, S)表示或有可转债在时间t的价值,其到期时间为T,面值为M,并在时间ti支付票息ci,其中i=1, 2, ..., n。如果股价在T之前降到预先设定的障碍水平SB,则或有可转债合约规定的触发事件发生。假设在时间t,触发事件还未发生。一旦触发事件发生,一定比例的面值αM将被转化为Cr=(αM)/Cp份股票,剩余部分被保留为面值为(1-α)M的债券直到或有可转债到期,即原来的票息降为(1-α)ci。此或有可转债的定价公式为

|
(18) |
其中

|
(19) |
其中:

|
(20) |
显然,当H=1/2和t=0时,这个定价公式变为De Spiegeleer和Schoutens研究中的式(36),所以,文章的定价公式可以看作是该研究提供的定价公式的扩展形式,在该研究中,标的股票价格服从几何布朗运动,即假定标的股票收益率序列不存在自相关,股价变化在时间上相互独立,这也是绝大多数衍生品定价文献的假设之一[1]。
由式(19)和式(20),可知市场均衡条件排除了条件均值对或有可转债价值的影响,从而可以专注于研究积分波动率对或有可转债价值的影响。
基于以上的或有可转债显式定价公式,可以很容易地对或有可转债价格进行敏感性分析,求出或有可转债的希腊字母。其中最重要的是Delta,即Δ(t, S)=∂V(t, S)/∂S,其在或有可转债的对冲中起着关键作用。但由于文章的重点在于推导分数布朗运动环境下或有可转债的显式定价公式,以及收益率自相关性对或有可转债价值的影响,从而不在此求解其希腊字母。
四、障碍期权的定价文中CoCos定价公式依赖于分数布朗运动环境下障碍期权和远期合约的定价公式,这些定价公式由如下定理给出。
定理2. Cdown-and-outH(t, S)表示向下敲出看涨期权在时刻t的价值,其到期时间为T,执行价格为K,障碍水平为SB且SB < K,到期支付为(ST-K)+1{St>SB, ∀t∈[0, T]};在当前时刻t∈[0, T],该障碍期权还未敲出。Pdown-and-outH(t, S)表示相应的向下敲出看跌期权的价值,到期支付为(K-ST)+1{St>SB, ∀t∈[0, T]}。则到期支付为(ST-K)1{St>SB, t∈[0, T]}的向下敲出远期合约的价值为

|
(21) |
其中:
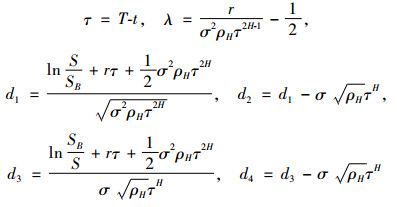
|
(22) |
证明:为了书写方便,令F(t, S)=Fdown-and-outH(t, S),则F(t, S)满足如下的偏微分方程

|
(23) |
其中:两个边值条件刻画了该远期合约的特性。
令① 
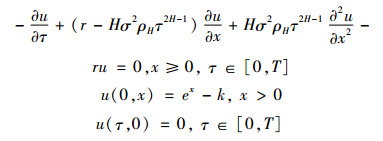
|
(24) |
令② η(τ, x)=x+α(τ), w(τ, η)=u(τ, x)eβ(τ),则

|
(25) |
令③ 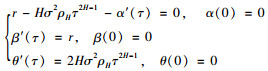
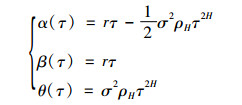
|
(26) |
并且以上的PDE变为
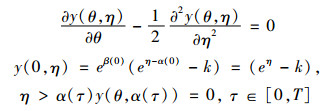
|
(27) |
式(27)的解如下[17]

|
(28) |
其中
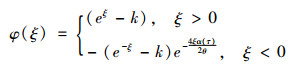
|
(29) |
从而有

|
(30) |
经计算可得
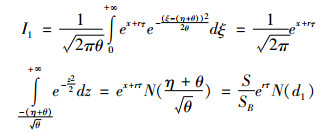
|
(31) |
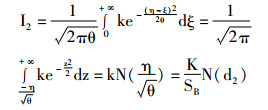
|
(32) |
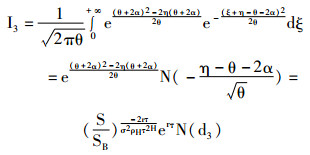
|
(33) |

|
(34) |
其中:z是标准正态随机变量。从而,
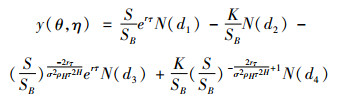
|
(35) |
所以,

|
(36) |
证毕。
定理3. Ddown-and-outH(t, S)表示向下敲出数字期权在时刻t的价值,其到期时间为T,执行价格为K,障碍水平为SB且SB < K,到期支付为1{St>SB, ∀t∈[0, T]};在当前时刻t∈[0, T],该障碍期权还未敲出。则

|
(37) |
其中:
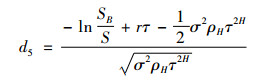
|
(38) |
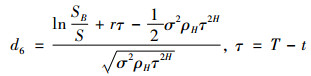
|
(39) |
证明:Ddown-and-outH(t, S)的偏微分方程与Fdown-and-outH(t, S)的一样,只是边值条件不同。为了简洁起见,令D(t, S)=Ddown-and-outH(t, S),则D(t, S)满足如下的偏微分方程
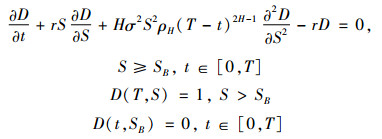
|
(40) |
作与定理2一样的三次变量替换,可得式(39)的解为
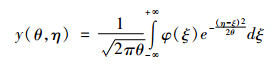
|
(41) |
其中:
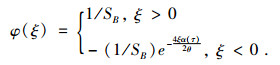
|
(42) |
从而,

|
(43) |
经计算可得
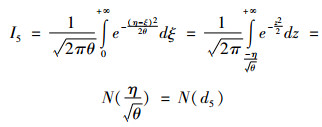
|
(44) |

|
(45) |
所以

|
(46) |
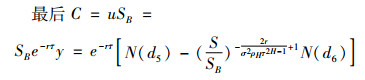
|
(47) |
证毕。
具有相同到期时间、执行价格、障碍水平的敲出障碍期权与敲入障碍期权的关系如下:
敲出障碍期权+敲入障碍期权=香草期权[18]。
由此,再根据定理2和定理3便容易得到向下敲入远期合约和向下敲入数字期权的定价公式。
定理4. Fdown-and-inH(t, S)表示向下敲入远期合约在时刻t的价值,其到期时间为T,执行价格为K,障碍水平为SB且SB < K,到期支付为(ST-K)1-1{St>SB, ∀t∈[0, T]};在当前时刻t∈[0, T],该远期合约还未敲入。则
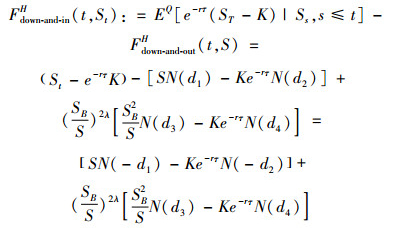
|
(48) |
定理5. Ddown-and-inH(t, S)表示向下敲入数字期权在时刻t的价值,其到期时间为T,执行价格为K,障碍水平为SB且SB < K,到期支付为1-1{St>SB, ∀t∈[0, T]};在当前时刻t∈[0, T],该障碍期权还未敲入。则

|
(49) |
其中:
注2:文章的CoCo定价公式依赖于障碍期权定价公式。但是,目前分数布朗运动环境下的障碍期权定价公式,都隐含地应用了“wick资产组合价值”的概念,如果令(Ft)t≥0表示障碍期权价值,则在以前的研究中,其满足如下的PDE

|
(50) |
如果式(17)被式(50)替代,则文章定理所示定价公式中的σ2ρH(T-t)2H将被σ2(T2H-t2H)替代,后者呈现的结果与金融直觉不相符[19]。
五、数值算例现在取或有可转债合约的参数如表 1所示,根据式(18)计算或有可转债的价格。假设股票不支付股息,或有可转债每年支付一次票息ci,且ci为常数,那么该如何设定票息率以使得或有可转债的首日发行价等于其面值?
|
|
表 1 或有可转债合约的参数[1] |
假设定票息率ci/M=3.64%,可得与De Spiegeleer和Schoutens一样的结果[1]。结果如下:V1=1 076.3,V2=-67.382 1,V3=-8.483 8和V=1 000.4。这表明De Spiegeleer和Schoutens研究中的CoCos定价公式是文章定价公式的一个特例,即在方程(17)中取H=1/2和t=0[1]。
令Hurst指数从0.5增加到0.65,而其他参数的取值与前一个例子保持一致,计算结果如表 2所示。取值H∈[0.5, 0.65]的原因是银行股票收益率序列的长程自相关性较弱。从表 2可知,或有可转债首日发行价随着Hurst指数从0.5增至0.65而减小。Hurst指数对衍生品价格的影响与衍生品的剩余到期时间τ有关。在文章的模型中,σ2ρHτ2H项表示标的股价从t到T的积分波动率(integrated variance),不妨记Ⅳ:=σ2ρHτ2H=σ2ρH(T-t)2H。积分波动率越大,相应的看涨期权、看跌期权等衍生品价格越高。在这个算例中,由于长程自相关性较弱,Hurst指数的取值不超过0.7,并且剩余到期时间较长,即τ=5,从而σ2ρHτ2H=:Ⅳ随着Hurst指数的增加而单调递增。所以,随着Hurst指数从0.5增至0.65,股价在或有可转债的续存期内触及障碍水平的概率增大,即触发事件发生的概率增大,从而或有可转债被自动转换成股票以及其面值被减记的可能性增加,从而或有可转债的价格随之下降。所以,当Hurst指数从0.5增至0.65时,为了使得或有可转债发行价等于其面值,需要提高票息率。
|
|
表 2 不同Hurst指数下CoCo及其组成部分的价值 |
从表 2可知,当Hurst指数从0.5增加到0.65时,V2和V3的绝对值随之上升,正是因为积分波动率σ2ρH(T-t)2H随之增大的缘故。但是,当H→1时,ρH→0;所以从理论上而言,当收益率序列的长程自相关性非常强的时候,积分波动率将随着Hurst指数增加到1而减弱为0。
此外,从表 2可得
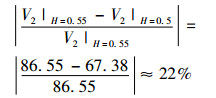
|
(51) |
和

|
(52) |
这表明,尽管银行股票收益率序列的长程自相关性较弱,但是它对或有可转债股权关联部分价值的影响非常显著。换言之,在发行或有可转债并为其定价时,如果用标准布朗运动代替分数布朗运动驱动标的银行股价的动态方程,则或有可转债股权关联部分的价值会存在很大的偏差。
注3:由式(51)和式(52)可知,标的股票收益率序列的长程相关性对障碍期权的价值影响显著。
六、结论与展望或有可转债作为一种重要的应急资本,可以提高银行在金融危机中的自救能力。随着越来越多的银行发行或有可转债,其定价模型亦成为热点。实证结果表明,在上交所交易的中资银行股票的对数收益率序列普遍存在较弱的长程自相关性、保持趋势性,股价存在长记忆性、分形性。文章首次将分数布朗运动引入到或有可转债定价模型中,标的股价动态方程由分数布朗运动驱动,其中分数布朗运动的Hurst指数H满足1/2 < H < 1,此过程能够刻画股价的长记忆性、分形性等非线性性质。
基于风险偏好假设得出障碍期权与远期合约的显式定价公式,与前人的研究相比,文章的障碍期权定价方法不使用“wick资产组合价值”的概念,定价公式不存在经济含义不清晰的问题。
笔者进一步给出或有可转债的显式定价公式。由于或有可转债是中长期金融衍生证券,虽然银行股价变动的长程自相关性较弱,但如果剩余到期时间较大,则该长程自相关性会显著提高或有可转债股权关联部分价值的绝对值,从而降低或有可转债价值。由于标的银行股票对数收益率序列的长程自相关性对或有可转债价值有明显的影响,从而应该给予考虑。
或有可转债是中长期金融衍生证券,可以继续考虑利率的随机性。在随机利率模型和分数布朗运动环境下,或有可转债以及相应的障碍期权定价公式可以作为文章的后续研究。
| [1] |
DE SPIEGELEER J, SCHOUTENS W. Pricing contingent convertibles:A Derivatives Approach[J]. Journal of Derivatives, 2012, 20(2): 27-36. DOI:10.3905/jod.2012.20.2.027 |
| [2] |
CORCUERA J M, SPIEGELEER J D, FAJARDO J, et al. Close form pricing formulas for Coupon Cancellable CoCos[J]. Journal of Banking & Finance, 2014, 42(3): 339-351. |
| [3] |
CORCUERA J M, FAJARDO J, SCHOUTENS W, et al. CoCos with extension risk. A structural approach[C]//PODOLSKIJ M. The fascination of probability, statistics and their applications. Switzerland: Springer, 2016: 447-464. https://link.springer.com/chapter/10.1007%2F978-3-319-25826-3_21
|
| [4] |
秦学志, 胡友群, 尚勤, 等. 基于转换点生存概率的或有可转债定价研究[J]. 管理工程学报, 2015, 29(2): 182-189. |
| [5] |
秦学志, 胡友群, 石玉山. 含股权回售与赎回条款的或有可转债定价研究[J]. 管理科学学报, 2016, 19(7): 102-114. DOI:10.3969/j.issn.1007-9807.2016.07.009 |
| [6] |
MANDELBROT B B. When can price be arbitraged efficiently?A limit to the validity of the random walk and martingale models[J]. Review of Economics & Statistics, 1971, 53(3): 225-236. |
| [7] |
PETERS E E. Chaos and order in the capital markets[M]. New York: Wiely, 1991: 13-208.
|
| [8] |
SHIRYAEV A N. Essentials of stochastic finance:Facts, models, theory[M]. Singapore: World Scientific Publishing Co. Ltd., 1999: 314-379.
|
| [9] |
范英, 魏一鸣. 基于R/S分析的中国股票市场分形特征研究[J]. 系统工程, 2004, 22(11): 46-51. |
| [10] |
郝清民. R/S系列分析的非线性估计及应用[J]. 系统工程理论与实践, 2005, 25(3): 80-85. DOI:10.3321/j.issn:1000-6788.2005.03.012 |
| [11] |
CHERIDITO P. Regularizing fractional Brownian motion with a view towards stock price modeling[D]. Zürich: Swiss Federal Institute of Technology, 2001.
|
| [12] |
CHERIDITO P. Arbitrage in fractional Brownian motion models[J]. Finance & Stochastics, 2003, 7(4): 533-553. |
| [13] |
WANG X T. Scaling and long-range dependence in option pricing Ⅰ:Pricing European option with transaction costs under the fractional black-scholes model[J]. Physica A Statistical Mechanics & Its Applications, 2010, 389(3): 438-444. |
| [14] |
ROSTEK S. Option pricing in fractional brownian markets[M]. Berlin: Springer, 2009: 79-110.
|
| [15] |
BJÖRK T, HULT H. A note on Wick products and the fractional Black-Scholes model[J]. Finance & Stochastics, 2005, 9(2): 197-209. |
| [16] |
XIAO W, ZHANG W, XU W, et al. The valuation of equity warrants in a fractional Brownian environment[J]. Physica A Statistical Mechanics & Its Applications, 2012, 391(4): 1742-1752. |
| [17] |
霍海峰, 温鲜, 邓国和. 分数次布朗运动的欧式障碍期权定价[J]. 经济数学, 2009, 26(4): 97-103. DOI:10.3969/j.issn.1007-1660.2009.04.014 |
| [18] |
WILMOTT P. Paul Wilmott on quantitative finance[M]. Chichester: Wiely, 2006: 390.
|
| [19] |
尤左伟, 刘善存, 张强. 混合分数布朗运动下可转债定价模型研究[J]. 系统工程理论与实践, 2017, 37(4): 843-854. |


