制造业面临向“多品种,小批量,短交期,低库存”转变,多品种小批量生产是企业为了适应消费者的多样化需求而采取的生产方式,根据需求来源的不同又可分为“按订单生产”和“按库存生产”,在各国的制造行业中,采用该种生产方式的企业都占有70%~90%的比重。按库存生产是传统的多样化生产方式,生产计划和生产活动容易实施;按订单生产是在需求多样化和产品快速迭代的背景下产生的,该生产方式生产的稳定性差,重复性低,生产效率低,生产成本高,不易流水线作业,给企业生产活动造成巨大困难。[1]
对于按订单生产的多品种小批量企业,它们在生产过程中需要关注的方面包括:生产柔性、生产计划、采购管理、库存控制、需求预测等。[2]其中,生产柔性、生产计划、库存控制、需求预测是内部因素,随着企业生产经营过程中的经验积累和管理能力的提高,这些方面会持续改进;多品种小批量的采购管理涉及数量繁多的外部供应商,不可控因素众多,是这类企业的管理难点之一,一旦在供应商采购的物料延迟交付,将影响企业生产计划安排,导致生产混乱,甚至企业产品的延迟交付,造成信誉损失和经济损失。[3]
在对多品种小批量制造企业的调研中了解到,该类型企业普遍面临供应商的延迟交付问题。供应商的延迟交付主要有以下两个原因:一是供应商主客观造成的不能按时交付;二是市场需求变化造成紧急采购,导致供应商交付时间短不能按时交付。[4]供应商的延迟交付可能导致生产制造环节计划变更、大量库存积压以及对客户的订单不能及时交付,企业面临失去客户和市场的巨大风险。[5]如果能够预测订单延迟交付的可能性,同时找到缩短产品总生产周期的关键因素,将为企业提供决策支持和改进策略。针对上述问题,文章利用数据挖掘技术,提出构建RELIEF-KNN(k-Nearest Neighbor)分类算法进行企业采购订单延迟交付风险的预测研究。[6]
二、RELIEF-KNN方法KNN算法是数据挖掘分类算法中常见算法之一。文章选用KNN分类算法作为基础,来进行采购订单延迟交付风险预测,是在充分验证了诸多分类算法(贝叶斯分类、K均值、支持向量机、人工神经网络等)的基础上,综合考虑算法的繁简度及预测效果来决定的。在预测效果相当的条件下,优先选择了KNN算法作为基础,用RELIEF方法对KNN进行改进。[7]
随着数据维数的增加,特征空间的体积指数增加,从而导致各方面的计算成本增加,人们称之为维数灾难。高维空间中,较小的噪声便足以掩盖住样本的本质区别,并且更多的无用特征不仅无助于提高分类效率和效果,反而会导致分类性能下降。[8]因此,提取相关度大的特征、剔除无效特征对于构造分类器来说十分关键。
在传统的KNN分类算法中,每个最近邻样本都有相同的投票权,对分类结果的影响程度没有区别,这使得算法的分类效果对最近邻个数k的选择很敏感。而事实上,这k个最近邻样本也有伯仲之分,距离待分类样本越近的最近邻样本理所应当该拥有较高等级的投票权。基于此,降低分类效果对k的敏感度的一种有效途径就是根据每个最近邻与待分类样本的相似程度来赋予不同权重,相似性越高,权重越大。
RELIEF算法最早由Kira提出,其初衷便针对于两类数据的分类问题。[9]Kononenko等对该方法进行了扩展和完善,使方法更加可靠。[10]RELIEF算法是一种特征权重算法,它根据样本的各个属性和类别的相关性来赋予属性不同的权重。同时,在得到所有样本属性的权重后,可以考虑将权重小于某个阈值的属性移除。将相关性低的属性过滤掉,一方面减少了分类算法的计算量,另一方面也有助于提高分类的准确性。因此,在传统KNN算法之前加入RELIEF算法进行属性筛选和权重计算,能够有效地减少无意义的计算,提高KNN分类器的稳定性。
在RELIEF算法中,属性和类别的相关性是基于属性对近距离样本的区分能力,简单地说,就是若在某属性上易于将样本进行区分,则给予该属性较高权重,否则给予该属性较低权重。实际操作过程为:
(1) 假定训练集D中有两类样本D0和D1,从D中随机选择一个样本x,假设其所属类别为D0。
(2) 计算样本x与D0和D1中其他所有样本的相似性。
(3) 在D0中提取x的k个最近邻样本,记为H,同时在D1中提取x的k个最近邻样本,记为M。
(4) 根据以下规则更新每个属性的权重:如果x和H在某个属性上的距离小于x和M在该属性上的距离,则说明该属性对区分D0和D1这两类样本的最近邻是有益的,因此,增加该属性的权重;反之,如果x和H在某个属性上的距离大于x和M在该属性上的距离,则说明该属性对区分D0和D1这两类样本的最近邻起相反作用,以此,降低该属性的权重。
(5) 将以上过程重复m次,最后汇总得到各属性的平均权重。最终所得的属性权重越大,表示该属性的分类能力越强,反之,表示该属性的分类能力越弱。
(6) 根据所得权重在分类效果方面的表现,划定权重的阈值,将权重低于某阈值的属性过滤掉,只留下有与类别关系紧密的属性用于KNN分类算法的计算中。
RELIEF算法的运行时间随着样本的抽样次数m和原始特征个数N的增加线性增加,因而运行效率非常高。
三、物料采购的延迟交付预测应用文章将RELIEF-KNN算法应用于多品种小批量物料采购订单的延迟交付预测中,为了便于观察和分析结果,首先以模架型芯类别为例,介绍从数据筛选,属性特征提取,延迟交付预测的全过程。
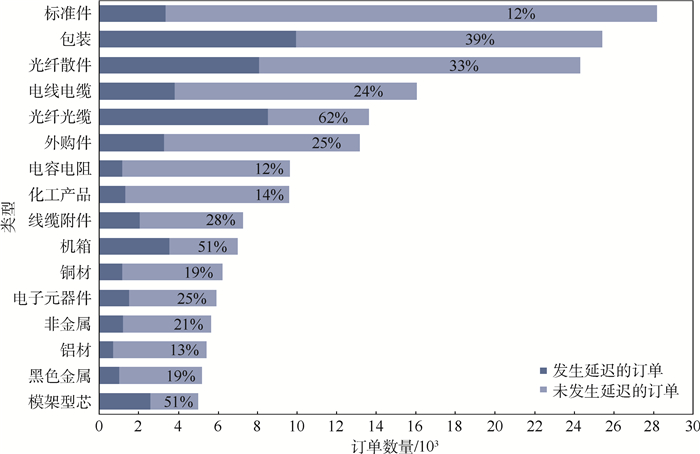
(一) 数据筛选研究采用国内某多品种小批量光纤零部件制造企业,根据公司供应商管理部提供的2013—2014两年的采购数据进行研究,共计约18.5万条订单记录。不同类型物料采购订单的数量及延迟交付率如图 1所示。
|
图 1 不同类型物料采购订单的延迟交付柱状图 |
2013—2014年模架型芯采购订单比较完整的采购记录共计5 013条,其中,2 575项采购发生了延迟交付情况,2 438项采购未发生延迟交付情况。每条采购记录包含“类别(模架型芯)、等级、材料代码、厂家代码、供方状态、单位性质、TS状态、ROH状态、W18状态、AH供应商、供货状态、数量、采购提前期”共计13个样本属性和“最终到货情况(延迟与否)”1个类别标签。其中,“供方状态、单位性质、TS状态、ROH状态、W18状态、AH供应商、供货状态”7项是表征供应商特征的变量。
数据预处理包括以下几项:
(1) 由于订单的采购批量为离散的数值型数据,属性值变化范围非常大,无益于后序的分类处理,因此,需要将采购批量的值做预处理,将其取自然对数。
(2) 采购提前期:采购提前期=最终到货情况(计划)-送货审核日期(订单下达日期),延迟1天交付的订单视为未发生延迟。
(3) 最终到货情况:属性值为文本型数据“0”和“1”,用“0”表示该订单发生了延迟交付,用“1”表示该订单未发生延迟交付。
(4) 每个样本都用一个14维向量x表示,x=(x1, x2, …, x13, b),其中xi为样本属性值(分别为类别、等级、材料代码、厂家代码、供方状态、单位性质、TS状态、ROH状态、W18状态、AH供应商、供货状态、数量、采购提前期),b表示样本的类别标签(最终到货情况为准时或延迟)。
(二) 属性特征提取将模架型芯类的所有采购订单按1:2的比例随机分为两组,其中,数量较多的一组记为训练集D,共3 326条采购样本,数量较少的一组记为测试集T,共1 687条采购样本。训练集可以看作已经交付的历史采购订单,这些数据包含着丰富的采购信息,被用来构建KNN分类模型。用构建好的分类模型来对测试集的样本的类别标签进行预测,并将预测结果与测试集中订单的实际交付情况进行对比,以评价分类的准确性。
将训练集D按订单是否发生延迟交付划分为两组D0和D1,其中每条样本都包含了13个属性值和1个类别标签。在D0中随机抽取一个样本x,如为x=[1, 183, 564, 3, 6, 3, 1, 1, 1, 2, 5, 1, 0],将x与D0、D1中的其他样本一一对比,记录每一个样本与x的相似度值。因为所有样本的1~11个属性的属性值均为文本型数据,12~13个属性为数值型数据,因此,根据“Jaccard相似性”与“欧几里得距离”的定义,样本x与di的相似性s的计算公式为
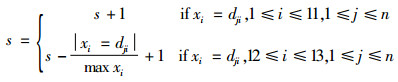
|
(1) |
随机样本x与其他样本的相似度矩阵如表 1所示,以其1中样本x与d3为例,两个样本的第1~11个属性中有7个完全相同,相似度暂时记为7,样本x的数量为5,样本d3的数量为8,数量属性最大的属性值为17,二者的欧几里得距离为|5-8|/17=0.176,相似度值为1-0.176=0.824,同理,可计算出在提前期属性上二者的相似度为0.928,所以样本x和d3的相似度值为7+0.824+0.928=8.752。部分相似度的计算结果如表 2和表 3所示。
|
|
表 1 随机样本x与其他样本的相似度矩阵 |
|
|
表 2 D0中x的k(k=10)个最近邻样本 |
|
|
表 3 D1中x的k(k=10)个最近邻样本 |
将各样本与x的相似度值按从高到低的顺序进行排列,在D0和D1中分别选取相似度值最大的k个样本,这2k个样本即作为样本x的最近邻样本。
接下来通过样本x的2k个最近邻样本来计算样本各属性的权重。
记样本属性的权重向量为W=(w1, w2, …, w13),初始化各属性权重wi=0(i=1, 2, …, 13)。
在属性i(i=1, 2, …, 13)上,若D0中的k最近邻与样本x的相似性小于D1中的k个最近邻与样本x的相似性,则说明该属性不利于将x划分到D0类(实际上x属于D0类),则将该属性的权重减1;反之,若D0中的k最近邻与样本x的相似性大于D1中的k个最近邻与样本x的相似性,则说明该属性有利于将x划分到D0类(实际上x属于D0类),则将该属性的权重加1;若二者相似性相等,则权重保持不变。例如:样本x的第2个属性(等级,属性值为文本型数据)值为1,其D0中的k个最近邻样本中有8个样本与x相似,亦为1,则相似性值记为8;其D1中的k个最近邻样本中有9个样本与x相似,属性值为1,则相似性值记为9。显然,样本x在第2个属性上与D1中的样本更接近,因此,将第2个属性的权重w2减1。在x的第12个属性(数量,属性值为数值型数据)值为5,其D0中的k个最近邻样本全部与x相似,亦为5,则相似性值记为10,其D1中的k个最近邻样本中有9个样本与x相似,属性值为5,有一个最近邻样本属性值为6,则相似性值为9-|5-6|17+1=9.94。显然,样本x在第12个属性上与D0中的样本更接近,因此,将第2个属性的权重w12增加|10-9.94|/10=0.004。
将所有随机抽取的样本x计算一遍,得到累加后的各属性权重向量W,将W各分量标准化后即可得到最终的属性权重向量。
在模架型芯采购订单中,分别抽取了D0样本量的10%作为x,每次选取x的10个最近邻样本进行属性特征权重的计算,得到的每个属性特征的权重如表 4所示。
|
|
表 4 各属性特征的权重向量 |
权重越高,说明该属性在KNN分类算法中越有利于将样本进行正确分类。从表 4可知,各属性权重在不同采购类型中有不同的分布情况,这说明对于不同类型的采购订单,影响其交付情况的因素有所差别。例如:对于包装类采购件来说,厂家的选择很重要,对于电子元器件来说,采购的批量对订单交付情况的影响较大。其中,样本属性的权重若不大于0,说明该属性特征对于利用KNN最近邻分类方法正确分类没有起到积极作用,因此,在构造分类器时可以不考虑这些属性特征。这样做在提高算法分类准确性的同时,也有助于减少数据的计算量,降低计算成本。
(三) 延迟交付预测在获得各属性的权重向量后,便可以利用训练样本中隐藏的信息对检测样本的标签进行预测。
1.提取检验集T的第一个样本t1,同上述RELIEF算法中一样,将t1与训练集D中的每一个样本一一进行比较,并计算t1与第i个样本di的相似性值si1。
2.根据样本的相似性值由高到低选取样本t1的10个最邻近样本。如t1=[14, 1, 183, 564, 3, 6, 3, 1, 1, 1, 2, 5, 1, 0], 其10个最近邻样本如表 5所示。
|
|
表 5 应用RELIEF-KNN获取10个最近邻样本 |
3.将以上10个最近邻样本按标签为“0”还是“1”划分为两组D01、D11,计算每一组最近邻样本的累计相似度值,即
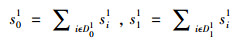
|
(2) |
4.领导或专家可根据自身风险偏好或管理目标需要设定一个阈值p。若p1=s01/s11≥p,则判定检测样本t1最可能具有类标签“0”,即该订单最可能发生延迟交付现象,必须采取一定措施进行管理;反之,则判定检测样本t1最可能具有类标签“1”,即该订单最可能不会发生延迟交付现象。
5.此外,由于决策者的风险偏好不同,也可以不设定阈值p,而输出检测样本t1的类标签为“0”或“1”的概率,决策者根据此概率自行衡量订单延迟风险大小。定义任意采购订单ti的延迟交付概率为

|
(3) |
其中:w10=59.66,w11=47.6,p1=55.77%。对于风险中性的决策者来说,将阈值p设定为50%,p1≥p,则判定该订单t1会发生延迟交付。而t1的真实标签确实为“0”,因此,该订单能够被正确预测。但对于风险偏好的决策者来说,若将阈值p设定为60%,pi < p,则该订单会被错误预测为不会发生延迟。
以模架型芯为例,计算阈值p与订单预测结果之间的关系,结果如表 6所示。阈值p的高低与订单预测结果的各项指标有紧密关系。若阈值设定的较高,则能够识别出的会发生延迟交付的订单量会减少,但准确性较高;若阈值设定的较低,则能够识别出的会发生延迟交付的订单量会增加,但准确性会降低。
|
|
表 6 阈值p与订单预测结果之间的关系 |
四、结论
文章从多品种小批量企业物料采购问题出发,提出用RELIEF-KNN算法进行物料采购延迟交付预测。RELIEF方法通过提取相关度大的特征、剔除无效特征,有助于提高KNN分类效率和效果。研究结果表明,文章提出的RELIEF-KNN方法能够合理提取属性特征,预测结果稳健,为多品种小批量物料采购延迟交付预测提供了一条有效途径。
| [1] |
李海珠. 如何在多品种小批量特点的生产环境下开展供应管理[J]. 物流工程与管理, 2015, 37(6): 135-136. |
| [2] |
施云. 多品种小批量产品供应管理的策略研究[J]. 物流工程与管理, 2010, 32(7): 80-81. |
| [3] |
温友良, 韩刘侠, 王海恒, 等. 生产能力评估与风险管理协同策略探索[J]. 价值工程, 2011, 30(4): 109-110. |
| [4] |
刘卫宁, 郑林江, 孙棣华, 等. 射频识别在多品种小批量生产管理中的应用研究[J]. 计算机工程与应用, 2010, 46(27): 1-11. DOI:10.3778/j.issn.1002-8331.2010.27.001 |
| [5] |
尹超, 张飞, 李孝斌, 等. 多品种小批量机加车间生产任务执行情况可视化动态监控系统[J]. 计算机集成制造系统, 2013, 19(1): 46-54. |
| [6] |
陈关亭, 黄小琳, 章甜, 等. 基于企业风险管理框架的内部控制评价模型及应用[J]. 审计研究, 2013(6): 93-101. |
| [7] |
彭春华, 刘刚, 相龙阳, 等. 基于Relief相关性特征提取和微分进化支持向量机的短期电价预测[J]. 电工技术学报, 2013, 28(1): 277-284. |
| [8] |
余忠华, 吴昭同. 面向多品种、小批量加工过程的统计质量控制应用策略与方法的探讨[J]. 系统工程理论与实践, 1999, 19(7): 128-131. |
| [9] |
KIRA K, RENDELL L. The feature selection problem: Traditional methods and a new algorithm[C]//AAAI Press, 1992: 440-446.
|
| [10] |
KONONENKO I. Overcoming the myopia of inductive learning algorithms with RELIEFF[J]. Applied Intelligence, 1997, 7(1): 39-55. DOI:10.1023/A:1008280620621 |


