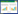Owing to the increasing demand for high-speed and ultraprecision motion, various positioning systems driven by linear motors are widely used in industrial applications [1]. These systems, based on ironless permanent magnet synchronous linear motors (IPMSLMs), exhibit the advantages of high speed-thrust ratio, unlimited travel, and no transmission error [2, 3]. However, compared with the servo motor, IPMSLM is more sensitive to various force disturbances owing to the reduction of gear transmission.

The improvement of the servo performance of precision positioning systems, on one hand, depends on the properties of each mechanical part and the assembly accuracy, and on the other hand, relies on the control algorithm and anti-disturbance characteristic. The disturbance, which varies during the movement, is nonlinear and thus, hard to measure and model. A traditional proportion-integralderivative (PID) control algorithm cannot handle nonlinear disturbances effectively, especially for systems driven by linear motors. Therefore, a disturbance observer (DOB) is proposed to estimate the lumped disturbance by the difference between the output of the inverse nominal model and the control input [4]. Yan et al. [5] proposed a digital DOB included in the feedback-feedforward control structure to compensate the undesired nonlinearity and external load disturbance of the direct drive system. Zhang et al. [6] designed a DOB as a feedback compensator to compensate the force disturbance based on the disturbance model, and its performance was better at high speeds. Cho et al. [7] developed a periodical adaptive DOB, assuming that all the measured states and disturbances were periodic and repetitive, and it could compensate for the disturbances whose frequency components are below and above the bandwidth of the Q-filter of the DOB.

Contrary to other spurious noises, friction can be modeled, and it accounts for a large part of the disturbance. Therefore, the modeling, identification, and compensation of friction have been studied in depth [8-11]. However, as friction is difficult to measure directly, it can be estimated using other physical quantities. DOB [12] and experiment are two friction measuring methods. The DOB contains other noises besides friction, and the data obtained must be processed using complicated procedures to separate friction from other disturbances. In addition, friction can be acquired by experimental means, such as circuit loop [13], velocity loop, and positioning error [14]. There are several friction models commonly used, such as Stribeck friction model (SFM) [15], LuGre model, and Maxwell model [10]. The accuracy of complex parameter identification determines the accuracy of the friction model, which indicates that the estimation algorithm plays a dominant role in the process [16, 17]. Chen et al. [16] proposed an intelligent glowworm swarm optimization algorithm to identify the friction parameters and the convergence can be hastened only using a finite time parameter estimation law and nonlinear sliding mode technique. Harman et al. [18] developed an online input estimation method, based on which an online friction compensator with a good dynamic performance was designed. Piatkowski [19] presented a method for determining the parameters of LuGre and Dahl dynamic models, and it employed a numeric optimization. Lin et al. [20] proposed particle swarm optimization (PSO), genetic algorithm, and real-coded genetic algorithm-based optimization to evaluate the parameters of the nonlinear friction model, achieving a good positioning accuracy. Kabziński and Jastrze ˛bski [21] designed an estimation method using the operating amount of ultra-low speed experiments.

The dynamic friction model is comparatively complex, and its parameter identification is so complicated that the result is difficult to estimate. Moreover, the methods for determining friction are sometimes inaccurate. Massive experiments have demonstrated that the positioning error is closely related not only to the velocity, but also to the position of the worktable. Based on the above considerations, this paper proposes a modified SFM, the values of which are indicated by analog voltage. Furthermore, a parameter optimization algorithm based on the initial identification result of least squares method (LSM) is developed, exhibiting the advantages of shorter convergence time and higher identification accuracy. The design of friction compensator closely corresponds to the experimental data gathering. The effectiveness of the modified SFM, optimization algorithm, and compensator can be verified using experiments.

A long-stroke ultra-precision XY positioning platform for nano-imprinting is shown in Fig. 1. The stage features a long range of 500 mm × 500 mm and high repeatability of 2 μm. The platform adopts the H-type mechanism owing to its capacity for heavy load and low torque during the long movement. The bottom layer is driven by dual IPMSLMs, whereas the upper layer is driven by a single IPMSLM. Incremental linear grating sensors with a resolution of 0.1 μm are selected for position inspection and feedback. In addition, in order to improve the efficiency and synchronization of the system, two digital hall sensors are used at the bottom layer. The Elmo driver is used and the PMAC control card of Delta Tau is adopted in the motion controller.

Fig. 1 XY precision positioning platform

Figure options

During the movement, friction can be divided into several sections according to the change of velocity, and the division principle is comparatively complex [20, 22]. SFM, which is the most commonly used friction model, can be expressed as Eq. (1).

(1)

where represents the velocity of the platform, F_s the maximum static friction, F_c the Coulomb friction, v_s the SFM critical velocity, B the viscous friction coefficient, and δ the Stribeck shape factor, which is generally 2 [14].

Owing to the influence of installment inaccuracy of guide rails and other mechanic assembly errors, the force varies at different positions. Accordingly, a modified SFM is proposed and expressed as Eq. (2). According to the identification experiments and data analysis, F_s is a constant, whereas the values of F_c and B are different at different positions, which can be explained by the deformation of the guide rail, installation errors after measuring the straightness of the guide rail, and the parallelism between the linear motor and guide rail. Owing to the restrictive relation between the speed and motion time at a given position interval, F_c and B can be described as the piecewise function of x, representing the position of the worktable.

(2)

According to the control algorithm shown in Fig. 2, the position loop and velocity loop close in the PMAC, whereas the circuit loop closes in the driver. The signal, outputted by the PMAC to the driver from the digital to analog converter (DAC) port, is the analog voltage varying from -10 V to 10 V. The analog voltage is adjusted by the circuit loop and the final output is used to control the movement of the stage. The process can be expressed by the block diagram shown in Fig. 2.

Fig. 2 Control flow diagram of the system

Figure options

During the positioning process, the force condition is expressed as Eq. (3), where M represents the mass of the load driven by the IPMSLM, F_t the motor thrust, F_f the friction during the movement, the acceleration of the movement, and F₁ represents the other disturbances. F_t can be computed by Eq. (4), where K_c and K_t represent the circuit gain ratio and thrust coefficient, respectively, and V_out represents the output analog voltage of the PMAC. When the stage runs into a steady state (=0), F_t is equal to F_f regardless of other disturbances. Consequently, the friction of the system can be measured by the thrust of the motor. Considering the linear relationship between V_out and F_t, V_out, rather than F_t, is collected to perform the friction analysis, and thus, the influence of environment and motor noises can be avoided effectively.

(3)

(4)

We obtain the output analog voltage V_out for different positive velocities from 0 to 50 mm along the y-axis. After performing median filtering to eliminate the data with a gross error, the voltage-velocity curve can be obtained, as shown in Fig. 3. According to the SFM curve, the experimental graph is approximately consistent with the standard curve. This also indicates that the aforementioned method to represent friction using V_out is valid.

Fig. 3 The curve of output analog voltage and velocity

Figure options

In order to acquire the modified SFM of the system, it is necessary to perform parameter identification, which significantly influences the compensation accuracy. Therefore, after the initial identification result acquired by the LSM in MATLAB, we propose an optimal identification algorithm—a recursive algorithm (RA)—based on the minor difference between the identification result and the experimental result. The RA is illustrated as follows.

Step 1  Each iteration vector Θ_i consisting of four parameters (as shown in Eq. (5)), is substituted into Eq. (2), and Eq. (6) is obtained supposing that the platform moves in a positive direction, namely > 0, where i represents the iteration time with an initial value of 0, j the number of velocity samples varying from 1 to n, and F'_i(v_j) the modeled friction in each iteration. Θ₀ is obtained from the identification result with LSM. The difference △F_i(v_j) between the experimental friction and modeled friction is calculated by Eq. (7).

Step 2  Owing to the aforementioned minor difference, △F_i(v_j) can also be expressed as Eq. (8), where A_{i, j}, B_{i, j}, C_{i, j}, and D_{i, j} are expressedas Eq.(9). △F_ci, △F_si, △v_si, and △B_i are the computed values in each iteration and can be calculated by Eq. (10). In each iteration time, △F_i(v_j), A_{i, j}, B_{i, j}, C_{i, j}, and D_{i, j} are the vectors comprising of n members.

Step 3  Θ_i+1=(F_c(i+1), F_s(i+1), v_s(i+1), B_(i+1), ) is the initial value of the subsequent iteration and each member is computed by Eq. (11). The iteration will not end until a better identification result is obtained.

The evaluation of each iteration effect depends on the values of root-mean-square error (RMSE, Re) and R-squared, and they can be computed using Eqs. (12) and (13), respectively. The best identification result features a smaller value of RSME and larger R-squared simultaneously

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

The results of RA computed by MATLAB programming are shown in Table 1. The result of the third iteration is selected according to the judgment principle. Although the R-squared value of the sixth iteration is larger, it deviates from the experimental data, and thus can be ignored.

Table 1 Results of each iteration

Table options

The position interval is 50 mm in the experiment. Theoretically, the smaller the interval, the more accurate the model. However, the analog voltage, representing the friction, cannot be obtained precisely in an ultra-short period of time at a high speed. The experimental values and the corresponding fitting curves in each interval are shown in Fig. 4. There might be some minor differences between Fig. 3 and Fig. 4(f) although they are in the same measuring range, resulting from the change of environment. After parameter identification and optimization, the parameters of the modified SFM are listed in Table 2.

Fig. 4 The experimental values and fitting curves of each position interval

Figure options

Table 2 Parameter identification results

Table options

The control algorithm of the system is illustrated in Fig. 5. It adopts a combination of discrete PID, velocity feedforward, acceleration feedforward, and Coulomb friction feedforward algorithms, among which the feedforward can effectively decrease the following error. However, in order to handle the disturbances during the movement, a friction compensator, as shown in Fig. 6, is designed. Owing to the shorter servo update period of 408 μs, it is possible that the sign of velocity, actual velocity, and actual position are the three parameters inputted to the modified SFM. The actual velocity can be obtained using a low-pass first order discrete filter (E(1 -z^-1) shown in Fig. 5) after obtaining the actual position, in which E(1 -z^-1)=T_sw/(1 +z^-1+T_sw), T_s represents the servo update time of the system and w represents the cutoff frequency. Compared with inputting the command velocity and command position, this method can significantly improve the dynamic tracking error. The value of friction compensation is added to V_out; hence the data compensating port closely corresponds to the data gathering port, avoiding the noise introduced by the environment and motor.

Fig. 5 Servo control algorithm of the system

Figure options

Fig. 6 Friction compensator design

Figure options

Pulse signals are used as the input and output signals in the system, and the system modeling involves the conversion from pulse to position, velocity, and acceleration. The conversion equation used for the servo loop modeling is Eq. (14), where D_vel represents the command velocity, D_acel the command acceleration, A_vel the actual velocity, F _error the following error, P_os the command position, n the servo period, and K_aff, K_vff, K_fff, K_p, K_i, and K_d the acceleration feedforward, velocity feedforward, friction feedforward, and the PID values, respectively.

(14)

The parameters of the motor and control algorithm are listed in Table 3. Load mass (representing the end load driven by the linear motor), pole pitch, viscous coefficient, phase inductance, thrust factor, peak circuit, and phase resistance are the motor parameters used in the motor simulation, whereas K_aff, K_vff, K_fff, K_p, K_i, and K_d are welladjusted controller parameters used in the simulation.

Table 3 Motor and servo loop parameter

Table options

To a large extent, the positioning accuracy depends on the accuracy of velocity tracking. Therefore, the velocity loop is simulated in this sector instead. In the simulation system, the input of velocity loop is a step signal of 9 mm/ s. The simulation results with and without adding the friction disturbance at 200 ms are shown in Fig. 7, in which the friction disturbance is a step signal with a value of 20 N provided by the linear motor specification and its step time is 200 ms. The velocity drops by 9.6% with the friction, which demonstrates that the friction influences the performance of movement. Figure 8 shows the simulation results without compensation, with DOB compensator, and with friction compensator. Compared with non-compensation, the velocity of the DOB compensator increases by 5.19%, and the velocity of the friction compensator increases by 10.66% after a minor drop, as shown in the zoomed-in area with a red circle. Consequently, the proposed friction compensator achieves a better performance.

Fig. 7 Velocity response comparison curve

Figure options

Fig. 8 Comparison curves of two compensators

Figure options

By measuring the positioning error during the linear motions along the y-axis from -250 mm to 150 mm for different velocities from 0.1 m/s to 0.5 m/s, the errorvelocity curve obtained is shown in Fig. 9. It can be observed from the curve that the positioning error varies with the change of velocity. The main disturbance closely related to velocity is the friction along the movement. Thus, it can be concluded that the friction has a considerable influence on the positioning error. Accordingly, modeling and compensation of the friction are necessary to improve the platform performance.

Fig. 9 Relationship between positioning error and velocity along y-axis

Figure options

The PMAC provides an open servo algorithm for users, and this function can be realized in two languages—assembly language and programmable logic controller (PLC). In the experiment, since PLC0 has the highest interruption priority compared to the others, the compensation program can be written to PLC0 and visited every three servo cycles. Hence the compensation value can be updated dynamically in order to realize real-time friction compensation.

The worktable performs a linear move from 0 to 50 mm at lower speed and higher speed, respectively. The following errors are selected when the motor steps into a steady state move. At the speed of 0.005 m/s (as shown in Fig. 10), the following errors with the Coulomb friction compensation, traditional SFM compensation, and modified SFM compensation are 10.683 μm, 5.886 μm, and 3.454 μm, respectively, indicating that the following error of the modified SFM decreased by 67.67% compared with the Coulomb friction compensation. Furthermore, at the speed of 0.05 m/s (as shown in Fig. 11), the following errors with the Coulomb friction compensation, traditional SFM compensation, and modified SFM compensation are 7.803 μm, 6.211 μm, and 3.774 μm, respectively, indicating that the following error of the modified SFM decreased by 51.63% compared with the Coulomb friction compensation. The jitter of the tracking errors results from the system performance with higher rigidity and lower damping. Thus, it can be concluded that the modified SFM based compensator improves the dynamic properties significantly.

Fig. 10 Comparison curves at a speed of 0.005 m/s

Figure options

Fig. 11 Comparison curves at a speed of 0.05 m/s

Figure options

The worktable performs a cosine move at the speed of 0.01 m/s with an acceleration time of 500 ms from -50 mm to 50 mm along the y-axis, and its motion expression is . The actual cosine trajectory curve is shown in Fig. 12. During the movement, the following errors with the modified SFM compensation and the Coulomb friction compensation are compared in Fig. 13. It can be concluded from the curve that under the circumstance of each velocity reversal, the compensation effect is not significant, whereas the following error can be decreased from approximately 10 μm to 3 μm by applying the modified SFM compensation after a period of velocity reversals.

Fig. 12 Trajectory curve of cosine motion

Figure options

Fig. 13Comparison curves of following error for a cosine move

Figure options

In this paper, a modified SFM and a parameter optimization algorithm—RA are proposed, and a friction compensator is designed based on them. The inputs are the sign of velocity, actual velocity, and actual position, whereas the output value is a deviation that represents the friction and can be computed online. The simulation results in the velocity loop demonstrate that the friction compensator performs better than the DOB compensator owing to the velocity recovery of 10.66%. The experimental results show that the following error improves by 67.67% and 51.63% at lower and higher velocities, respectively. This improvement of following error is attributed to the high correspondence between friction data gathering and compensating, as well as the online computation of friction. Therefore, this method can be applied in the trajectory tracking movement with a rigid demand for tracking accuracy. However, the proposed modified SFM has a limitation in terms of velocity reversals. Further studies are being conducted to handle the pre-sliding problem, thus improving the tracking accuracy in the entire motion process.